Вероятности суммы и произведения событий

2.1. Два стрелка, вероятности попадания в мишень у которых равны соответственно 0,7 и 0,8, делают по одному выстрелу в одну мишень. Определить вероятности следующих событий:

-«в мишени будут два попадания»;

-«в мишени будет хотя бы одно попадание»;

-«попаданий в мишень не будет».

2.2. В двух урнах находятся шары, отличающиеся только цветом. В первой урне: 5 белых шаров, 11 чёрных и 8 красных. Во второй урне соответственно: 10,8 и 6. Из каждой урны наудачу извлекаются по одному по одному шару. Какова вероятность того, что извлечённые шары будут одинакового цвета?

2.3. В урне находится шаров с номерами от 1 до . Шары извлекаются наудачу

по одному без возвращения. Какова вероятность того, что при первых 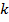извлечениях номера появившихся шаров совпадут с номерами извлечений ?

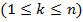2.4. Вероятность наступления некоторого случайного события в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до наступления этого события. Определить вероятность того, что: а) придётся проводить четвёртый опыт; б) будет проведено четыре опыта.

2.5. Три стрелка одновременно стреляют по одной мишени. Вероятности попадания при одном выстреле соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что при одновременном залпе этих стрелков в мишени будет: а) только одно попадание; б) хотя бы одно попадание.

2.6. Из урны, содержащей шесть белых и четыре чёрных шара, наудачу последовательно по одному извлекаются шары до первого появления шара чёрного цвета. Найти вероятность того, что придётся производить четвёртое извлечение, если шары берутся: а) без возвращения; б) с возвращением в урну после фиксирования его цвета.

2.7. Вероятность того, что изготовленная на первом станке деталь будет первосортной равна 0,7. Для детали, изготовленной на втором станке, эта вероятность равна 0,8. На первом станке изготовлены две детали, на втором – три. Найти вероятность того, что все пять деталей будут первосортными.

2.8. Определить вероятность того, что наудачу выбранное натуральное число: а) не делится ни на два, ни на три; б) не делится или на два, или на три.

2.9. На пяти карточках написано по одной букве так, что они составляют слово «колос». Карточки перемешиваются, а затем раскладываются наудачу снова в ряд. Какова вероятность того, что получится слово «сокол»?

2.10. На шести карточках написано по одной букве так, что они составляют слово «карета». Карточки перемешиваются, а затем раскладываются наудачу снова в ряд. Какова вероятность того, что получится слово «ракета»?

2.11. Для сигнализации об аварии установлены два работающих независимо друг от друга сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95, а того, что сработает второй сигнализатор – 0,9. Найти вероятность того, что: а) при аварии сработает только один сигнализатор; б) при аварии сработает хотя бы один сигнализатор.

2.12. Абонент забыл последнюю цифру номера телефона, а потому набирает её наудачу. Определить вероятность того, что ему придётся звонить не более чем в три места.

2.13. Из урны, содержащей два чёрных и два белых шара, два игрока поочерёдно без возвращения извлекают шары. Выигрывает тот, кто первым извлечёт белый шар. Найти вероятности выигрыша для каждого из игроков.

2.14. Два игрока подбрасывают по две монеты. Выигрывает тот, у которого выпадет больше гербов. В случае выпадения равного числа гербов 14 подбрасывания продолжаются до первого положительного результата. Определить вероятности выигрыша игры для каждого игрока. Какова вероятность того, что игрок A выиграет игру при третьем бросании? Какова вероятность того, что игроки сделают ровно три бросания? Какова вероятность того, что игроки сделают больше трёх бросаний?

2.15. Три орудия поочерёдно стреляют по одной мишени до первого попадания в неё. Вероятности попадания при одном выстреле у них равны соответственно: 0,6; 0,5 и 0,4. Определить вероятность того, что цель будет поражена, если каждое орудие может сделать не более трёх выстрелов. Какова вероятность того, что цель будет поражена при четвёртом выстреле? Какова вероятность того, что на поражение цели будет израсходовано не более трёх снарядов?

2.16. В коробке находятся 6 катушек с белыми нитками, 4 катушки с чёрными нитками и 2 катушки с красными нитками. Катушки извлекаются по одной без возвращения. Определить вероятность того, что катушка с белыми нитками появится раньше катушки с чёрными нитками.

2.17. Из полной колоды карт (52 штуки) последовательно по одной извлекаются три карты, причём карта чёрной масти сразу возвращается в колоду, а карта красной масти – не возвращается. Определить вероятность того, что третья извлечённая карта будет красной масти.

2.18. В урне находятся шаров с номерами от 1 до . Наудачу проводится извлечений по одному шару с возвращением извлечённого шара после фиксирования его номера в урну. Определить вероятность того, что ни один шар не появится более одного раза.

2.19. В обществе, состоящем из 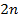человек, одинаковое число мужчин и Места за круглым столом занимаются наудачу. Определить вероятность того, что два лица одного пола не займут места рядом.

2.20. В урне находятся одинаковых шаров, из которых - белого, а - чёрного цвета . Производятся подряд без возвращения извлечений по два шара. Определить вероятность того, что каждый раз извлекались пары шаров разного цвета.

2.21. В урне имеются два шара – белый и чёрный. Производятся извлечения по одному шару до тех пор, пока не появится чёрный шар, причём при извлечении белого шара этот шар возвращается в урну и при этом добавляются ещё два белых шара. Определить вероятность того, что при первых пятидесяти извлечениях чёрный шар не будет извлечён.

2.22. Игрок 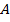поочерёдно играет с игроками и 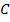, имея вероятность выигрыша в каждой партии 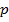, и прекращает игру после первого проигрыша или после двух партий, сыгранных с каждым игроком. Определить вероятности выигрыша игры и 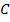. Как изменяются вероятности выигрыша всей игры для каждого из игроков, если

2.23. Из урны, содержащей n шаров с номерами от 1 до , последовательно извлекают два шара, причём первый шар возвращается, если его номер не равен единице. Определить вероятность того, что шар с номером 2 будет извлечён при втором извлечении.

2.24. Студент успел выучить 20 из 25 вопросов программы. Зачёт считается сданным, если студент ответит не менее чем на три из четырёх предложенных вопросов программы. Какова вероятность того, что: а) студент сдаст зачёт; б) зачёт будет сдан, если он правильно ответит на первые два вопроса и хотя бы на один из двух оставшихся; в) зачёт будет сдан, если известно, что на первые два из четырёх вопросов он уже дал правильные ответы?

Дата добавления: 2015-08-21