Геометрические вероятности

5.1. В круг, радиус которого равна , наудачу бросается точка. Возможность попадания точки в любую область круга не зависит от места положения области в круге и пропорциональна лишь площади этой области. Какова вероятность того, что расстояние от точки до центра круга будет меньше, чем половина длины радиуса?

5.2. В круг, радиус которого равна , наудачу бросается точка. Возможность попадания точки в любую область круга не зависит от места положения области в круге и пропорциональна лишь площади этой области. Какова вероятность того, что эта точка окажется внутри вписанного в круг квадрата?

5.3. На плоскости проведены параллельные прямые, расстояния между которыми попеременно равны 1,5см и 8см. Определить вероятность того, что наудачу брошенный на плоскость круг радиуса 2,5см не пересечёт ни одной линии.

5.4. Два человека договариваются о встрече. Первый приходит в любое время между 12.00 и 12.30 и ждет 20 минут. Второй приходит в любое время между 12.10 и 12.50. Найти вероятность того, что они встретятся.

5.5. В круге радиуса параллельно заданному направлению проводятся хорды. Какова вероятность того, что длина наудачу проведённой хорды будет не более чем 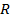, если равновозможны любые положения точек пересечения хорды с диаметром перпендикулярным заданному направлению?

5.6. Из наудачу выбранной на полуокружности точки на диаметр опускается перпендикуляр. Какова вероятность того, что длина этого перпендикуляра будет меньше, чем половина длины радиуса?

5.7. В круге радиуса наугад выбирается точка. Из этой точки, перпендикулярно отрезку, соединяющему точку с центром круга, проводится хорда. Какова вероятность того, что длина этой хорды не превосходит ?

5.8. На отрезке длиною наудачу выбраны две точки, в результате чего этот отрезок оказался разделённым на три части. Определить вероятность того, что из трёх получившихся частей можно построить треугольник.

5.9. Какова вероятность того, что сумма длин трёх наудачу взятых отрезков, длина каждого из которых не превосходит , будет больше ?

5.10. На отрезке 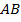длиною наудачу поставлены две точки и . Найти вероятность того, что точка будет ближе к точке , чем к точке .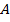

5.11. Какова вероятность того, что из трёх наудачу взятых отрезков, длина каждого из которых не превосходит , можно построить треугольник?

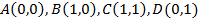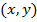5.12. В квадрате, вершины которого имеют координаты: ставится наудачу точка , координаты которой . Определить вероятность случайного события .

5.13. В шар вписан куб. Точка наудачу бросается в шар. Какова вероятность того, что точка попадет в куб?

5.14. В круге радиуса с центром в начале координат наудачу ставится точка . Пусть 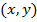- её координаты. Определить вероятность случайного события .

5.15. Около одной из двух окружностей, имеющих одинаковые радиусы, описан правильный треугольник. В другую окружность правильный треугольник - вписан. Что более вероятно: попасть наудачу брошенной точкой в часть треугольника, лежащую вне первой вписанной окружности, или в часть круга ограниченного второй окружностью и лежащую вне вписанного треугольника?

5.16. Два товарища договорились о встрече в течение промежутка времени . Тот, кто первым придёт на место встречи ждёт товарища не более минут. Определить вероятность того, что встреча состоится, если время прихода на место встречи каждого из них равновозможно в течение договоренного промежутка времени .

5.17. На окружности радиуса R наудачу поставлены три точки. Какова вероятность того, что получившийся треугольник будет остроугольным?

5.18. Из множества положительных чисел, которые не превосходят единицу, наудачу выбираются два числа. Определить вероятность того, что сумма квадратов этих чисел не превосходит число 0,75.

5.19. Начало прямоугольной системы координат находится в центре круга единичного радиуса. Определить вероятность того, что сумма абсолютных значений координат наудачу выбранной внутри круга точки не превосходит длины радиуса круга.

5.20. Начало прямоугольной системы координат находится в центре шара единичного радиуса. Определить вероятность того, что сумма абсолютных значений координат наудачу выбранной внутри шара точки не превосходит длины радиуса шара.

Дата добавления: 2015-08-21