Дискретная случайная величина

6.1. Опыт состоит в однократном бросании игральной кости. Для случайного числа выпавших очков на верхней грани построить: а) ряд распределения; б) многоугольник распределения; в) функцию распределения. Определить математическое ожидание и дисперсию числа выпавших очков.

6.2. Построить ряд распределения и функцию распределения случайного числа попаданий мячом в корзину при одном броске, если вероятность попадания мячом в корзину при одном броске равна 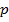. Определить математическое ожидание и дисперсию случайного числа попаданий при одном броске. При каком значении 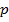значение дисперсии будет максимальным?

6.3. Из урны, содержащей пять белых и семь чёрных шаров, без возвращения извлекаются три шара. Для случайного числа появившихся белых шаров построить ряд распределения и определить его математическое ожидание. Чему равно математическое ожидание случайного числа появившихся чёрных шаров?

6.4. Из урны, содержащей пять белых и семь черных шаров, с возвращениями извлекаются три шара. Для случайного числа появившихся белых шаров построить ряд распределения и определить его математическое ожидание. Чему равно математическое ожидание случайного числа появившихся чёрных шаров?

6.5. Опыт состоит из трёх независимых подбрасываний монеты. Для случайного числа появившихся гербов построить: а) ряд распределения; б) многоугольник распределения; в) функцию распределения. Определить математическое ожидание и дисперсию случайного числа появившихся гербов.

6.6. Производится одинаковых, независимых опытов, в каждом из которых событие 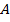может наступить с вероятностью 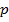. Постройте ряды распределений а) случайной величины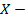

число появлений случайного события 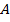и б) случайной величины число появлений случайного события противоположного событию 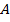. Найдите математические ожидания и дисперсии этих случайных величин.

6.7. Из коробки, содержащей 10 красных и 5 синих карандашей, случайным образом извлекаются четыре карандаша. Постройте ряд распределения и определите математическое ожидание случайного числа красных карандашей появившихся в выборке, если: а) карандаши извлекаются без возвращения; б) карандаши извлекаются с возвращением. Постройте ряд распределения и определите математическое ожидание случайного числа красных карандашей оставшихся в коробке при первом варианте извлечения.

6.8. Производятся последовательные независимые испытания пяти приборов на надёжность. Каждый следующий прибор испытывается только в том случае, если предыдущий прибор оказался надёжным. а) Построить ряд распределения случайного числа приборов, подвергшихся испытаниям, если вероятность выдержать испытание для каждого из них равна 0,8. б) Построить ряды распределения случайного числа приборов, успешно выдержавших испытания, и в) числа приборов, отказавших при испытании.

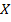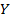6.9. Стрелок имеет шесть патронов и стреляет до первого попадания или пока у него есть патроны. Построить ряды распределения случайных величин и , где 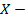число сделанных выстрелов, а число сделанных промахов, если вероятность попадания при одном выстреле равна p=0,7. Чему будет равно математическое ожидание случайной величины 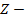число попаданий в мишень?

6.10. Игральную кость подбрасывают раз. Постройте ряд распределения и определите математическое ожидание и дисперсию случайного числа выпадений шестерки.

6.11. Из урны, содержащей белых и чёрных шаров, проводятся извлечения по одному шару с возвращением до тех пор, пока не появится белый шар. Найти математическое ожидание числа проведенных извлечений и математическое ожидание числа появившихся чёрных шаров.

6.12. Из урны, содержащей три белых и четыре чёрных шара, без возвращения извлекаются пять шаров. Построить ряды распределения случайных чисел появившихся белых и чёрных шаров. Определить их математические ожидания.

6.13. Два баскетболиста поочерёдно бросают мяч в корзину до тех пор, пока один из них не попадет. Построить ряды распределения случайных величин 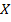и 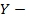количества бросков, произведённых каждым баскетболистом, если вероятности попаданий при одном броске для каждого из них равны соответственно и 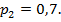Чему равна вероятность того, что у них будет одинаковое количество бросков?

6.14. Одновременно подбрасываются две игральных кости. Случайная величина 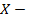сумма очков, выпавших на верхних гранях костей. Постройте ряд распределения случайной величины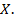

Определите математическое ожидание и дисперсию случайной величины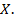

6.15. Производится три одинаковых независимых опыта. В каждом опыте с равными вероятностями может быть получено любое целое число от 0 до 3. Пусть число, полученное при проведении -того опыта (). Определить математическое ожидание и дисперсию случайной величины Построить ряд распределения случайой величины 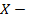суммы чисел, полученных в результате проведения трёх опытов . Определите математическое ожидание и дисперсию случайной величины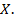

6.16. В лотерее разыгрываются: мотоцикл стоимостью 25 тыс. руб., три велосипеда стоимостью по 5000 руб. и шесть штук часов стоимостью по 500 руб. Найти математическое ожидание выигрыша на один билет, если общее число билетов равно 250. Какой процент от суммы, полученной от продажи билетов, останется у организаторов лотереи, если цена одного билета будет равна 350 рублей?

6.17. Два стрелка стреляют каждый по своей мишени, делая, независимо друг от друга, по одному выстрелу. Вероятности попаданий в мишень для каждого из стрелков равны соответственно 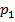и 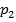. Рассматриваются случайные величины: 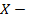число попаданий первого стрелка, число попаданий в мишень второго стрелка, и Постройте ряд распределения случайной величины 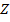и определите её математическое ожидание

6.18. Производятся два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 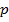. Рассматриваются случайные величины: 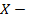разность между числом попаданий и числом промахов; 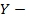сумма числа попаданий и числа промахов. Для каждой случайной величины постройте ряд распределения. Определите их числовые характеристики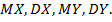

6.19. В корзине 4 яблока и 6 апельсинов. Случайным образом из нее выбирается 3 фрукта. Обозначим через 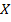случайную величину, равную количеству яблок среди выбранных фруктов. Найти: 1) ряд распределения и функцию распределения случайной величины 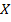; 2) математическое ожидание ; 3) дисперсию ; 4) вероятность события

6.20. В связке имеются восемь ключей, из которых только один подходит к замку. Для открывания замка наудачу выбирается один ключ из связки. Пусть 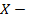число проб до открывания замка. Определите математическое ожидание если перед следующей пробой ключ, который не подошёл, в связку не возвращается.

Дата добавления: 2015-08-21