Средняя наработка до отказа. Средняя наработка между отказами

Средняя наработка до отказа – математическое ожидание наработки объекта до первого отказа. Обозначается T.

Если время есть непрерывная случайная величина: 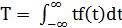. Из а следует, что 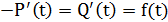,. C учетом этого, получаем: 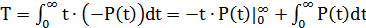, тут , поэтому получаем .

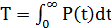Если время разделено на небольшие интервалы: 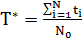, где – образцы вначале, отказ каждого элемента фиксируется.

Выберем интервал испытаний и через заданные постоянные промежутки времени определим значение: , где - число образцов, отказавших в этом интервале, 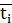– среднее время i-го интервала, – время, в течение которого отказали все образцов.

, где 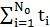– наработка между отказами, – число отказавших образцов.

6. Комплексные показатели надёжности. (Коэффициенты готовности, функция готовности, технического использования)

Комплексные показатели надёжности – коэффициенты, характеризующие соотношения между временем работы и временем простоя (восстановления), частоту профилактических мероприятий, влияние элементов, установленных в данную аппаратуру, на надёжность всей системы.

Функция готовности – вероятность того, что в момент времени t аппаратура или система является работоспособной. Статистически оценивается как: 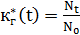, где – общее число изделий, установленных на испытание, – число изделий, находящихся в исправном состоянии в момент времени t.

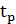Коэффициент готовности – вероятность того, что объект окажется в работоспособном состоянии в любой момент времени. Вероятностная оценка коэффициента готовности: , статистическая оценка: , где – время работы, 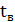– время восстановления. , где – вреднее время восстановления.

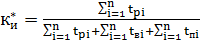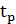Коэффициент технического использования – отношение математического ожидания интервалов времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к сумме математических ожиданий интервалов времени в работоспособном состоянии, простоев, обусловленных техническим обслуживанием и ремонтом за тот же период эксплуатации. Обозначается . , где – время работы, 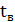– время восстановления, 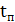– время простоя.

7. Показатели надёжности объектов для экспоненциального закона распределения времени возникновения отказов

Вероятность безотказной работы: 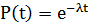, суммарная интенсивность отказов: , частота отказов: 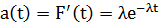, среднее время до первого отказа: 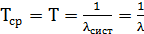, дисперсия: D = 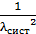. При 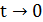: . При экспоненциальном законе средняя наработка до отказа – это то время, в течение которого вероятность безотказной работы системы уменьшается в е раз.

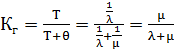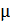Для восстанавливаемых систем: , где - интенсивность восстановления. Связь между 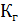и : .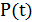

При t = 0: 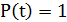, при : .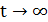

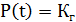8. Расчёт надёжности аппаратуры при внезапных отказах. Приближенный (прикидочный) расчёт надёжности по средней интенсивности отказов

В случае произвольного закона распределения времени исправной работы вероятность безотказной работы системы может быть записана в виде: , где – зависимость интенсивностей отказов элементов различных типов от времени, 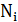– число элементов i-го типа в устройстве, k – чисто типов элементов. На практике пользуются . где 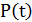– теория, – эксперимент, - количество испытуемых образцов, - число отказавших образцов за время t.

Приближенный расчёт надёжности по среднегрупповым интенсивностям отказов элементов: в качестве исходных данных должны быть известны количество элементов каждого типа и их интенсивности отказов. Для расчёта используется номограмма (график зависимости 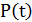), по которой можно определить: вероятность безотказной работы по известной наработке до отказа и заданной длительности работы; по известной или заданной вероятности безотказной работы и требуемой длительности работы t определять значения наработки а отказ или наработку до отказа; по известному значению и заданной вероятности безотказной работы находить время исправной работы t.

Расчёт надёжности с использованием данных из опыта эксплуатации: в качестве исходных данных должна быть известна наработка на отказ устройства, выбранного в качестве аналога, общее количество элементов в аналогичном устройстве 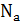, общее количество элементов в проектируемом устройстве 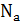. Суть состоит в том, что средняя интенсивность отказов проектируемого технического устройства и аналога полагается равной 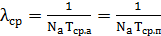. Ожидаемая наработка на отказ проектируемого устройства рассчитывается из выражения: .

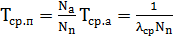9. Анализ надёжности систем с общим резервированием при идеальных переключателях

Вероятность безотказной работы резервированной системы кратности m для любого закона распределения при идеальных переключателях определяется рекуррентной формулой вида:

, где 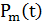– вероятность безотказной работы резервированной системы кратности m, – вероятность безотказной работы основной системы в течение времени , 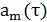– частота отказов резервированной системы кратности m в момент времени .

При экспоненциальном законе ненагруженном (холодном) состоянии резерва имеем: , , где и – интенсивность отказов и среднее время безотказной работы основного (нерезервированного) устройства.

При экспоненциальном законе и недогруженном (теплом) резерве имеем:

,

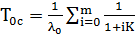
Где 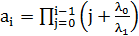, , 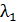– интенсивность отказов резервного устройства до замещения.

При экспоненциальном законе распределения и нагруженном состоянии резерва формулы для и совпадают с соответствующими формулами для горячего резерва целой кратности.

10. Расчёт надёжности при неодновременной работе отдельных блоков аппаратуры. Эффективность работы систем управления

Если отдельные части системы или элементы, входящие в блоки, работают неодновременно, их целесообразно объединять в группы по времени их работы и образовывать из данных групп соответствующие элементы расчёта. При этом считается, что интенсивность отказов выключенных элементов равна нулю, а старение элементов в указанном режиме отсутствует.

При неодновременной работе блоков устройства, состоящего из m блоков, его интенсивность отказов 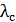является функцией времени. В этом случае для расчёта показателей надёжности используют формулу: , где

· – интенсивность отказов i-го блока

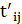· – момент j-го включения i-го блока

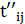· – момент j-го выключения i-го блока

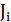· – общее количество включений блока за время работы

· – интенсивность отказов i-го блока.

Наработка до первого отказа .

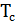Величины и определяют соответственно вероятность безотказной работы и среднее время наработки устройства до отказа. Значение суммы, стоящей в показателе экспоненты, соответствует величине интенсивности отказов устройства .

Дата добавления: 2015-08-21