Методика расчета надежности технической аппаратуры методом графов

Методика применяется для сложных систем с восстановлением. Требования:

· система обладает конечным (счетным) числом состояний;

· время работы непрерывно;

· эволюция системы описывается марковским (полумарковским) процессом.

Марковский процесс – процесс без последействия, т.е. для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние.

Реальные системы имеют конечное множество состояний (n+1):

· H₀,.., H_n-1 – работоспособные

· H_n – отказовое

Если система без восстановления, то отказовое состояние H_n называется «поглощающее», иначе называется «отражающее».

1. Марковский однородный случайный процесс в момент времени t характеризуется вероятностью P_i(t) пребывания системы в состоянии H_i.

Интенсивности переходов из состояния H_i в H_j обозначаются как λ_ij = const.

В графах P_i(t) являются вершинами, λ_ij ребрами.

2. Полумарковский случайный процесс характеризуется:

· F_i(t) – функция распределения времени пребывания системы в состоянии H_i;

· П_ij(t) – вероятность перехода из состояния H_i в H_j в момент выхода при условии, что она находилась в состоянии H_i в момент времени t.

В графах F_i(t) являются вершинами, П_ij(t) ребрами.

i

P_i(t)

λ_k

λ_k+1

λ_m

P_k

λ_m+1

P_k+1

Правило составления уравнений по графу:

Пример 1.

Система без восстановления, вероятность перехода из рабочего состояния H₁ в поглощающее состояние H₂ подчиняется экспоненциальному закону. Процесс однородный марковский.

Распределение времени возникновения отказов:	P1(t) P2(t) λ
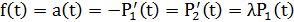
Пример 2. Система с восстановлением	P1(t) P2(t) λ μ

Решение:

Коэффициент готовности где

· среднее время восстановления

· среднее время безотказной работы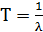

Тогда решение::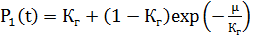

Дата добавления: 2015-08-21