Потоки отказов. Простейший поток отказов и его свойства. Ведущая функция и параметр потока отказов

Для восстанавливаемых объектов эксплуатация может быть описана следующим образом: в начальный момент времени объект начинает работу и работает до отказа, после отказа происходит восстановление работоспособности, объект вновь работает до отказа и т.д. (при этом время восстановления не учитывается). Для таких объектов моменты отказов на оси суммарной наработки или на оси непрерывного времени образуют поток отказов.

В качестве показателя безотказности таких объектов используют ведущую функцию данного потока - математическое ожидание числа отказов за время t: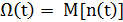

Параметр потока отказов – отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки: или

где М - символ математического ожидания, n(t) - число отказов за время t.

Параметр потока отказов нельзя отождествлять с понятиями «средняя частота отказов» и «интенсивность потока отказов».

Простейший поток отказов – это такой поток, при котором время возникновения отказов удовлетворяет одновременно условиям стационарности, отсутствия последействия и ординарности.

Стационарность случайного процесса – времени возникновения отказов – означает, что на любом промежутке времени Dt вероятность возникновения n отказов зависит только от п и величины промежутка Dt, но не изменяется от сдвига Dt по оси времени.

Если случайный процесс стационарный, то большое число наблюдений, сделанных над одной системой в произвольно выбранные моменты времени, имеет те же статистические свойства, что и то же число наблюдений, но сделанных одновременно над большим числом систем (эргодическое свойство).

Отсутствие последействия означает, что вероятность наступления n отказов в течение промежутка времени Dt не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Это условие для систем с большим числом элементов означает, что отказ любого элемента системы не приводит к изменению надежности остальных элементов, т.е. отсутствуют корреляционные связи между временами отказов отдельных элементов. Тогда поток отказов называется потоком без последействия, если для любых не перекрывающихся участков времени число отказов, попадающих на один из них, не зависит от числа отказов, попадающих на другие. Условие отсутствия последействия означает, что отказы являются событиями случайными инезависимыми.

Ординарность потока отказов означает невозможностъ появления в один и тот же момент времени более одного отказа.

Свойства простейшего потока отказов

· случайные события, образующие простейший поток, распределены по закону Пуассона, т.е. ;

· плотность вероятности промежутков времени от начала потока до k-того события определятся как ;

· если промежуток времени, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части промежутка: он будет таким же, как и закон распределения всего промежутка;

· сумма большого числа простейших потоков в течение времени t образует такой же простейший поток и интенсивностью Λ, равной сумме интенсивностей составных потоков в течение того же времени t, т.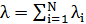е. , где – интенсивность составных потоков, N – число простейших потоков.

Дата добавления: 2015-08-21