Оценка неизвестных параметров законов распределения. Доверительный интервал, метод максимума правдоподобия

Точное теоретическое значение параметров распределения, например , практически никогда не известно, однако при наличии большого статистического материала можно оценить значение параметра , которое применимо в качестве оценки теоретического значения .

Рассеивание случайной величины около мат ожидания – дисперсия.

Любое значение числовой характеристики распределения, полученного на основе ограниченной статистики содержит материал случайности.

Приблизительное случайное значение будет называться оценками числовых характеристик :

Поскольку исходная случайная величина – это время до отказа, распределяемое по нормальному закону, то и сама оценка будет распределена по тому же закону.

Для получения оценок и доверительных границ используется метод максимума правдоподобия и метод наилучших нормальных оценок.

Доверительный интервал - термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительно при небольшом объёме выборки. Доверительным называют интервал , который покрывает неизвестный параметр с заданной надёжностью p: .

Имеем случайных вектор с координатами … , распределение вероятности которого зависит от параметра Θ. Этот параметр считается неслучайной величиной, сохраняется при всех испытаний одного и того же неизменного значения.

Двухсторонним доверительным интервалом параметра Θ с коэффициентом доверия не меньше j называется случайный интервал 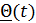и , концы которого . Концы зависят от исходов наблюдений … для любого значения τ > 0.

j – вероятность, что случайный интервал накроет наш теоретический параметр.

Доверительный интервал содержит больше сведений об объекте, чем , которое дает точное значение без указания на погрешность этого значения.

Примеры применения.

Для больших значений выборки, где n > 50, вероятность j с достаточной для практики точностью может быть величина при любых функциях распределения. На основе ЦПТ Ляпунова равняется:

Вероятность попадания любой случайной величины , подчиненная нормальному закону распределения с параметрами
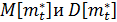в интервал для нормального закона

, , то есть .

Для нормального закона приближенные границы Т находятся из уравнений:

Дата добавления: 2015-08-21