
Читайте также:
|
Определение слагаемых входящих в выражение (9) приведено в таблице:
Таблица 3
| Исходные данные | I тон | II тон | ||||||||
| λ, с-1 | 6,476 | 16,112 | ||||||||
| Функция формы шпации: 19–20 fj (а) 19–20 fj (x) |
|
| ||||||||
| Nj, кН/мм | 20,338 | 306,912 | ||||||||
| χj | 0,1 | 0,1 | ||||||||
| Расчет | ||||||||||
| ω 2/ λj 2 (ω = 6,15) | 0,9018 | 0,1457 | ||||||||
| 1– ω 2/ λj 2 | 0,0982 | 0,8543 | ||||||||

| 0,1401 | 0,8601 | ||||||||

| 0,7009 | 0,9932 | ||||||||

| 0,7138 | 0,1163 | ||||||||
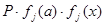 , кН , кН
| 3,733 | 10,837 | ||||||||

| 2,8493 | 263,975 | ||||||||

| 1,3101 | 0,041 | ||||||||
 ,мм ,мм
| 0,9182 | 0,0407 | ||||||||
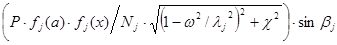 ,мм ,мм
| 0,9351 | 0,0048 |
Перемещение в шпации равно:
W (t)= 0,9589 cos ωt +0,9399 sin ωt
W (t) можно представить в виде:
W (t)= C cos(ωt–γ)
Используя формулу косинуса разности двух углов, получим:
A = C cos γ B = C sin γ
A =0,9589 B =0,9399



γ =44°42 ’
Тогда  окончательно примет вид:
окончательно примет вид:
W (t)= 1,34 cos(6,15 t– 44°42 ’)
W max=1,34 мм
Максимальная амплитуда колебаний в районе теоретических шпангоутов составляет 1,34 мм.
Допустимая амплитуда колебаний
α= 
Где: α – предельно допустимая амплитуда колебаний
n – число колебаний в секунду, т.е. частота в герцах
n=  =0,979
=0,979
N – число колебаний в минуту
1,926>1,34– максимальная амплитуда колебаний не превышает допустимую.
Дата добавления: 2015-08-21; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теоретическая часть | | | Модификатор Edit Mesh |