Метод Релея—Папковича

Метод Релея—Попковича дает достаточно точное значение частот и форм поперечных колебаний первых тонов. Идея метода основывается на положении о допустимости пользоваться вместо точных форм колебаний приближенными, поскольку погрешность при этом оказывается незначительной.

Функцию формы вертикальных колебаний корпуса П. Ф. Попкович выбрал в виде некоторой сдвинутой и повернутой относительно горизонтальной оси синусоиды:

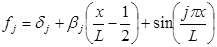(1)

где δ_j и β_j — сдвиг и угол поворота оси синусоиды, которые определяются из условий динамического равновесия:

(2)

Формы колебаний f_j (x) должны удовлетворять условиям динамического равновесия (2). Конкретный вид этих уравнений можно получить, если подставить ряд последовательно в первое и второе уравнение системы (2). Главная координата φ_j представляет собой гармоническую функцию φ_j (t)= A_j cos(λ_jt + α_j), тогда:

и система (2) запишется в виде:

Из последнего выражения следуют окончательные условия равновесия:

Подставляя в указанные уравнения формы колебаний согласно (1) и заменяя интегрирование приближенным суммированием по 20-ти ординатам, получим систему 2-х линейных алгебраических уравнений для определения неизвестных параметров δ_j и β_j. Система будет выглядеть следующим образом:

(3)

где: m ̅ _i — относительные интенсивности масс

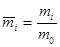
m_i — масса судна с присоединенной массой воды в районе i -го сечения, приходящаяся на единицу длины, т/м;

m ₀ — произвольная величина той же размерности, введенная для удобства вычислений.

Корпус по длине разбивают на 20 шпаций, и на протяжении каждой шпации интенсивность масс судна m_i, а также момент инерции сечения I_i считаются постоянными.

Составление коэффициентов уравнений (3), решение их и вычисление функций формы колебаний f_i выполняется в табличной форме (таблица 1).

Частота собственных изгибных колебаний определяется по формуле Релея:

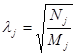(4)

где: N_j — обобщенный коэффициент жесткости;

M_j — обобщенная масса.

(5)

Интенсивность масс присоединенной воды при вертикальных колебаниях вычисляется по приближенной формуле:

где: ρ — плотность воды;

F — площадь погруженной части шпангоута в рассматриваемом сечении;

y — ордината (полуширина) ватерлинии в том же сечении;

d — осадка судна в том же сечении;

L, B — соответственно длина и ширина судна;

k — безразмерный коэффициент, равный для колебаний:

первого тона….. 0,10

второго тона….. 0,07

Дата добавления: 2015-08-21