Расчетная часть. Составление коэффициентов уравнений (3) сведено в таблицу 1.

Первый тон:

Составление коэффициентов уравнений (3) сведено в таблицу 1.

Получаем систему:

150,892 δ ₁ + 1,651+110,694=0

1474,687 δ ₁ – 163,204 β ₁+1097,656=0

Решение системы:

δ ₁= – 0,735

β ₁= 0,088

Тогда форма колебаний с учетом (1) и решением системы для 1-го тона будет выглядеть следующим образом:

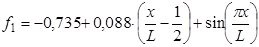
Коэффициент обобщенной жесткости согласно (5):

Обобщенная масса согласно (5):

Частота собственных колебаний по уравнению (4):

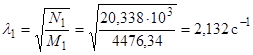
Поправки на сдвиг и вращение по (7):

Частота собственных колебаний 1-го тона с поправками на вращение и сдвиг согласно (6):

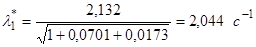
После расчетов строим форму собственных колебаний корпуса для 1-го тона (рисунок 1).

Второй тон:

Составление коэффициентов уравнений (3) сведено в таблицу 2.

Получаем систему:

138,925 +1,441 β ₂-1,789 =0

1359,488 δ ₂ – 151,275 β ₂+406,225=0

Решение системы:

δ ₂= – 0,013

β ₂=2,564

Тогда форма колебаний с учетом (1) и решением системы для 2-го тона будет выглядеть следующим образом:

Коэффициент обобщенной жесткости согласно (6):

Обобщенная масса согласно (5):

Частота собственных колебаний по (4):

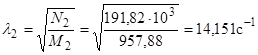
Поправка на сдвиг и вращение по (7):

Частота собственных колебаний 1-го тона с поправками на вращение и сдвиг согласно (6):

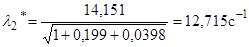
После расчетов строим форму собственных колебаний корпуса для 2-го тона (рисунок 2).

Рисунок 1

Рисунок 2

Дата добавления: 2015-08-21