
|
Читайте также: |

түріндегі бөлшектерді «үздіксіз бөлшектер» деп айтады. Бұндай бөлшектерде  санына алымы 1 бөлшек қосылады, ол бөлшектің бөлгішіндегі
санына алымы 1 бөлшек қосылады, ол бөлшектің бөлгішіндегі  санына алымы 1 бөлшек қосылады да, бұл бөлшектің бөлшегіндегі
санына алымы 1 бөлшек қосылады да, бұл бөлшектің бөлшегіндегі  санына тағы алымы 1 бөлшек қосылады т.с.с. осылайша кете береді. Мұндағы
санына тағы алымы 1 бөлшек қосылады т.с.с. осылайша кете береді. Мұндағы  сандары тұтас дұрыс сандар болады (
сандары тұтас дұрыс сандар болады ( саны 0 – тең бола алады).
саны 0 – тең бола алады).
Үздіксіз бөлшектегі  мағыналы бөлшектерді жасағыш бөлшектер деп атайды. Егер жасағыштар ақырсыз көп болса, оларды ақырсыз бөлшектер деп, жасағыштары санама болса, оны ақырлы бөлшек дейді.
мағыналы бөлшектерді жасағыш бөлшектер деп атайды. Егер жасағыштар ақырсыз көп болса, оларды ақырсыз бөлшектер деп, жасағыштары санама болса, оны ақырлы бөлшек дейді.
Жоғарыда жазылған бөлшекті
( )
)
түрінде жазуға да мүмкін.
Мысалы,  бөлшегін (3, 2, 4, 5) деп жазуға болады.
бөлшегін (3, 2, 4, 5) деп жазуға болады.
Теорема1. Әрбір ақырлы үздіксіз бөлшекті маңызы өзімен тең болатын кәдімгі бөлшек түріне аударуға болады.
Дәлел. Өйткені әрбір үздіксіз бөлшек шынында қосу және бөлу амалдарынан құралмақшы, сондықтан оның жасағыш бөлшектері санамалы болған күнде олардың аралығындағы көрсетілген қосу және бөлу амалдарын кашан да болсын орындап бітіруге мүмкін. Ол амалдардың қорытындысында әрине бір кәдімгі бөлшек жасалуы айқын нәрсе.
Мысал.
Бізге

түріндегі үздіксіз бөлшек берілсін. Оның ішіндегі амалдарды басынан орындап бітірелік.
Онда
1)  2)
2)  3)
3) 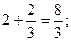 4)
4)  5)
5) 
бөлшегіне тірелдік. Сонымен берілген үздіксіз бөлшектің маңызы түріндегі кәдімгі бөлшекпен тең екендігі білінеді.
Теорема2(кері теорема): Әрбір дұрыс мәнді кәдімгі бөлшекті өзімен маңызы тең үздіксіз бөлшек түріне аударуға болады.
Дәлел. Бізге  мағыналы бөлшек берілсін. Оның ішінен тұтас сандарын шығарсақ, онда
мағыналы бөлшек берілсін. Оның ішінен тұтас сандарын шығарсақ, онда

теңдігі орындалып, мұнда a – тұтас еселік, t – маңызы x - ті y – ке бөлгендегі қалатын айырмаға тең болар еді. Егер де  бөлшегінің ішінде тұтас сандар жоқ болса, онда a = 0 шарты орынды болып, t = x теңдігі жасалмақшы.
бөлшегінің ішінде тұтас сандар жоқ болса, онда a = 0 шарты орынды болып, t = x теңдігі жасалмақшы.
Енді біз  бөлшегінің екі мүшесін де t – ге бөлсек, онда
бөлшегінің екі мүшесін де t – ге бөлсек, онда

теңдіктері орындалмақ. Мұнда  саны y -ті t -ге бөлгенде шығатын тұтас еселік болып,
саны y -ті t -ге бөлгенде шығатын тұтас еселік болып,  қалатын айырма болмақшы.
қалатын айырма болмақшы.
Енді  бөлшегінің екі мүшесін де
бөлшегінің екі мүшесін де  - ге бөлсек, онда
- ге бөлсек, онда

теңдігі шығады. Мұнда да  саны t – ны
саны t – ны  - ге бөлгендегі жасалатын тұтас еселік және
- ге бөлгендегі жасалатын тұтас еселік және  қалатын айырма болсын.
қалатын айырма болсын.
Бұл жолды  бөлшегін де және бұнан кейінгі жасалатын бөшектерге үзбей қолданып отырсақ, ақырында берілген
бөлшегін де және бұнан кейінгі жасалатын бөшектерге үзбей қолданып отырсақ, ақырында берілген  бөлшегі
бөлшегі

түріндегі үздіксіз бөлшек өрнегін жасайтындығы дәлелденді. Мұнан теорема енді шешіліп отыр.
Жоғарғы тәсілімізде  сандары шынында x - ті y – ке, y –ті бірінші айырма t –ге, бірінші айырманы екінші айырмаға бөліп отырғанда жасалған тұтас еселіктер болып отыр. Сондықтан оларды үздіксіз бөлшектің еселіктері деп те айтады. Жаңағы тәсіл x пен y мағыналы екі санның ең үлкен жаңа еселіктерін табарда да қолданылатын еді.
сандары шынында x - ті y – ке, y –ті бірінші айырма t –ге, бірінші айырманы екінші айырмаға бөліп отырғанда жасалған тұтас еселіктер болып отыр. Сондықтан оларды үздіксіз бөлшектің еселіктері деп те айтады. Жаңағы тәсіл x пен y мағыналы екі санның ең үлкен жаңа еселіктерін табарда да қолданылатын еді.
Мысалдар:
1)  бөлшегін үздіксіз бөлшек түріне аударуға керек екен. Бұл жағдайда
бөлшегін үздіксіз бөлшек түріне аударуға керек екен. Бұл жағдайда

түрінде болмақшы.
2)  бөлшегін үздіксіз бөлшек түріне аудару керек. Бұл үшін үздіксіз бөлшектің еселіктерін табалық. Олар:
бөлшегін үздіксіз бөлшек түріне аудару керек. Бұл үшін үздіксіз бөлшектің еселіктерін табалық. Олар:
1) 33: 16 = 2, 16: 1 = 16 болуына керек(2,16). Сондықтан ізделген бөлшек

түрінде болатындығы мәлімделеді.
Дата добавления: 2015-09-03; просмотров: 600 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Annotation | | | Жуықтас бөлшектер |