Квадрат түбір шығару

Бізге 13-тен шаршы түбір шығару мәселесі берілсін. Бұл үшін біз төмендегі жобаны қолданалық: 1) 13-тің ішіне кіретін ең үлкен шаршылық түбір 3 болмақ, өйткені 4-ті алсақ, болып, оның шаршылық дәрежесі берілген саннан артып кетер еді.

1) Енді біз

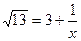(3.1)

теңдігі орынды болсын делік. Олай болса,

(3.2)

өрнегі арқылы

(3.3)

теңдігі орынды болады екен.

(3.3)-ші теңдіктің шамасы бір бөлшекті қосумен тең болатындығы үшін

(3.4)

теңдігін жасауға еріктіміз, онда

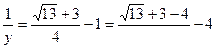
өрнегі арқылы

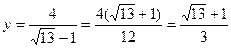(3.5)

теңдігі жасалмақ. Енді (5)-ші теңдіктің маңызын 1-ге бір бөлшек қосқанда тең болатындығып абайлап:

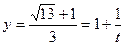(3.6)

өрнегін жасалық. Онда

(3.7)

өрнегі арқылы

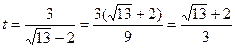(3.8)

теңдігі шықпақ. (3.8)-ші теңдікті жоғарғы жобамен

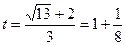(3.9)

түріне аударсақ, онда

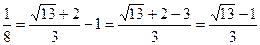
болып

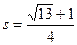
өрнегі табылады. Соңғы теңдікті

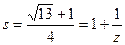
түріне аударып, онан

(3.10)

теңдігін табамыз. Соңғы теңдікте

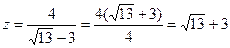(3.11)

өрнегі орындалмақ. (3.11)-ші өрнекті тағы да

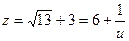(3.12)

түріне мінгізсек, одан

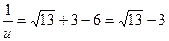(3.13)

теңдігі табылмақшы. (3.13)-ші теңдік пен (3.2)-ші теңдікті салыстырсақ яки 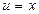екендігін білеміз. Олай болса, (3.1), (3.4), (3.6), (3.8), (3.9), (3.12) теңдіктері арқылы біз

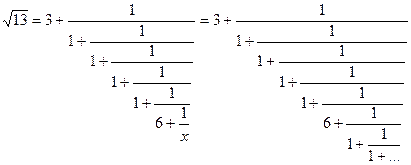(3.14)

бөлшегін жазуға еріктіміз. Мұнан енді 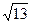- тің шаршы түбірі қиырсыз және қайталама үздіксіз бөлшектің түріне мініп отыр. Мұнда(1,1,1,1,6) еселігі қиырсыз қайталанып отырады екен. (3.14)-ші үздіксіз бөлшектің әрбәр жуықтас бөлшектері әрине 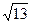- тің де жуықтас түбірлері болып отырмақшы. Олар:

түрінде болмақ.

§4. Үздіксіз бөлшектер арқылы айқындалған теңдеудің

Дата добавления: 2015-09-03