Бір пар түбірлерін шығару

Үздіксіз бөлшектер ережесі арқылы біз

(4.1)

түрдегі көмескі теңдеудің бір пар түбірін шығаруға еріктеміз. Мысалы, бізде

(4.2)

теңдеуі бар екен. Оны шешпестен бұрын біз бөлшегін үздіксіз түрге мінгізелік. Ал

(4.3)

түрінде болатындығы мәлім нәрсе. Енді соңғы үздіксіз бөлшектің аяғынан екінші жуықтас бөлшегін табалық (аяғынан бірінші жуықтас бөлшек берілген -нің өзі болатындығы белгілі). Ол шамасында болатындығы айқын. Табылған жуықтас бөлшегі жұп орында тұрғандағы үшін оның шамасы берілген ден артығырақ болып, арасындағы айырма шамасында болатын еді. Сондықтан

(4.4)

өрнегі жасалады. (4.4)- ші теңдікті берілген көмескі теңдеуге ұқсас қылу үшін соңғы теңдіктің бар мүшелерін 13-ке өсіріп, мына түрде жазалық , яки

(4.5)

Енді (4.5)-ші теңдік пен берілген теңдеуді салыстырсақ, тің орнына , тің орнына 39 алсақ, олар өзара дәл шығып отыр. Олай болса, теңдеуінің бір пар түбірі табылды, ол: . Сондықтан енді теңдеуінің бар түбірлерін табуға мүмкін.

Олар

тізімдері арқылы табылмақшы. санында шарт мәні болмайтындығы үшін, жоғарғы тізімде теңдеуін шарт қылсақ, түбір тізімдері мына сияқты қолайлы түрге мінбекші:

2-мысал: Бізде теңдеуі бар екен. 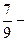ні үздіксіз бөлшекке аударалық. Онда

болмақ. Аяқтан екінші жуықтас бөлшекті табалық, ол 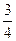екен. Алған жуықтасымыз тақ орында тұрғандығы үшін оның маңызы 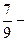ден кем болмақ. Сондықтан

Бұдан дәлдігі жасалады. Соңғы дәлдіктің мүшелерін 5-ке өсірсек өрнегі арқылы берілген теңдеудің бір пар түбірі табылады. Олар

Сондықтан берілген теңдеудің бар түбірлерінің мәні

тізімдерінен табылмақ.

саны шартты мәнге ие болатындығы үшін ні мен ауыстырсақ, алдыңғы тізімдер

түрлеріне мінеді.

Дата добавления: 2015-09-03