
Читайте также:
|
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -1,95 | 3,8025 | -7,41488 | 14,45900625 | ||
| 1,05 | 1,1025 | 1,157625 | 1,21550625 | ||
| 0,05 | 0,0025 | 0,000125 | 0,00000625 | ||
| 0,05 | 0,0025 | 0,000125 | 0,00000625 | ||
| 0,05 | 0,0025 | 0,000125 | 0,00000625 | ||
| 1,05 | 1,1025 | 1,157625 | 1,21550625 | ||
| -0,05 | 0,0025 | -0,00013 | 0,00000625 | ||
| 1,05 | 1,1025 | 1,157625 | 1,21550625 | ||
| 0,05 | 0,0025 | 0,000125 | 0,00000625 | ||
| 0,05 | 0,0025 | 0,000125 | 0,00000625 | ||
| 2,05 | 4,2025 | 8,615125 | 17,66100625 | ||
| -0,05 | 0,0025 | -0,00013 | 0,00000625 | ||
| 1,05 | 1,1025 | 1,157625 | 1,21550625 | ||
| -0,05 | 0,0025 | -0,00013 | 0,00000625 | ||
| -1,95 | 3,8025 | -7,41488 | 14,45900625 | ||
| 1,05 | 1,1025 | 1,157625 | 1,21550625 | ||
| -1,95 | 3,8025 | -7,41488 | 14,45900625 | ||
| 1,05 | 1,1025 | 1,157625 | 1,21550625 | ||
| 0,05 | 0,0025 | 0,000125 | 0,00000625 | ||
| 0,05 | 0,0025 | 0,000125 | 0,00000625 | ||
| Ср.зн. | 2,95 | 22,25 | -6,68325 | 68,331125 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 2,95
= 2,95
Стандартное отклонение вычисляется по формуле:
 = 1,08
= 1,08
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,2;
-0,2;
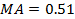 ;
;
 = -0,4;
= -0,4;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
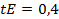 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 18
Вычисление показателей асимметрии и эксцесса для 6 класса (показатели по методике Басса-Дарки «Косвенная агрессия»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -1,7 | 2,89 | -4,913 | 8,3521 | ||
| -0,7 | 0,49 | -0,343 | 0,2401 | ||
| 2,3 | 5,29 | 12,167 | 27,9841 | ||
| -0,7 | 0,49 | -0,343 | 0,2401 | ||
| 0,3 | 0,09 | 0,027 | 0,0081 | ||
| 0,3 | 0,09 | 0,027 | 0,0081 | ||
| 1,3 | 1,69 | 2,197 | 2,8561 | ||
| 1,3 | 1,69 | 2,197 | 2,8561 | ||
| -0,7 | 0,49 | -0,343 | 0,2401 | ||
| -0,7 | 0,49 | -0,343 | 0,2401 | ||
| 0,3 | 0,09 | 0,027 | 0,0081 | ||
| 0,3 | 0,09 | 0,027 | 0,0081 | ||
| -1,7 | 2,89 | -4,913 | 8,3521 | ||
| -0,7 | 0,49 | -0,343 | 0,2401 | ||
| 1,3 | 1,69 | 2,197 | 2,8561 | ||
| 1,3 | 1,69 | 2,197 | 2,8561 | ||
| -0,7 | 0,49 | -0,343 | 0,2401 | ||
| 0,3 | 0,09 | 0,027 | 0,0081 | ||
| -1,7 | 2,89 | -4,913 | 8,3521 | ||
| 0,3 | 0,09 | 0,027 | 0,0081 | ||
| Ср.зн. | 2,7 | 24,2 | 4,32 | 65,954 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 2,7
= 2,7
Стандартное отклонение вычисляется по формуле:
 = 1,12
= 1,12
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 0,15;
0,15;
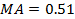 ;
;
 = -0,8;
= -0,8;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
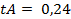 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 19
Вычисление показателей асимметрии и эксцесса для 6 класса (показатели по методике «Несуществующее животное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| 1,6 | -0,64 | -1,024 | -1,6384 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| -1,4 | 1,96 | -2,744 | 3,8416 | ||
| -1,4 | 1,96 | -2,744 | 3,8416 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| 0,6 | 0,36 | 0,216 | 0,1296 | ||
| 1,6 | 2,56 | 4,096 | 6,5536 | ||
| -1,4 | 1,96 | -2,744 | 3,8416 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| 1,6 | 2,56 | 4,096 | 6,5536 | ||
| -1,4 | 1,96 | -2,744 | 3,8416 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| 3,6 | 12,96 | 46,656 | 167,9616 | ||
| 2,6 | 6,76 | 17,576 | 45,6976 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| -1,4 | 1,96 | -2,744 | 3,8416 | ||
| -0,4 | 0,16 | -0,064 | 0,0256 | ||
| -1,4 | 1,96 | -2,744 | 3,8416 | ||
| 1,4 | 37,6 | 54,64 | 248,512 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 1,4
= 1,4
Стандартное отклонение вычисляется по формуле:
 = 1,4
= 1,4
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 0,9;
0,9;
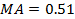 ;
;
 = 0,2;
= 0,2;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 20
Вычисление показателей асимметрии и эксцесса для 6 класса (показатели по методике Басса-Дарки «Физическая агрессия»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| 1,5 | 2,25 | 3,375 | 5,0625 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| -1,5 | 2,25 | -3,375 | 5,0625 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| 1,5 | 2,25 | 3,375 | 5,0625 | ||
| 1,5 | 2,25 | 3,375 | 5,0625 | ||
| -2,5 | 6,25 | -15,625 | 39,0625 | ||
| -0,5 | 0,25 | -0,125 | 0,0625 | ||
| -0,5 | 0,25 | -0,125 | 0,0625 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| 1,5 | 2,25 | 3,375 | 5,0625 | ||
| -0,5 | 0,25 | -0,125 | 0,0625 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| -1,5 | 2,25 | -3,375 | 5,0625 | ||
| 1,5 | 2,25 | 3,375 | 5,0625 | ||
| -0,5 | 0,25 | -0,125 | 0,0625 | ||
| -1,5 | 2,25 | -3,375 | 5,0625 | ||
| 2,5 | 6,25 | 15,625 | 39,0625 | ||
| -0,5 | 0,25 | -0,125 | 0,0625 | ||
| -1,5 | 2,25 | -3,375 | 5,0625 | ||
| Ср.зн. | 2,5 | 35,25 | 3,375 | 124,3125 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 2,5
= 2,5
Стандартное отклонение вычисляется по формуле:
 = 1,2
= 1,2
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 0,09;
0,09;
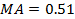 ;
;
 = -0,14;
= -0,14;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 21
Вычисление показателей асимметрии и эксцесса для 6 класса (показатели по методике Басса-Дарки «Косвенная агрессия»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| -0,6 | 0,36 | -0,216 | 0,1296 | ||
| -0,6 | 0,36 | -0,216 | 0,1296 | ||
| 1,4 | 1,96 | 2,744 | 3,8416 | ||
| -0,6 | 0,36 | -0,216 | 0,1296 | ||
| -0,6 | 0,36 | -0,216 | 0,1296 | ||
| -0,6 | 0,36 | -0,216 | 0,1296 | ||
| 1,4 | 1,96 | 2,744 | 3,8416 | ||
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| 2,4 | 5,76 | 13,824 | 33,1776 | ||
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| -0,6 | 0,36 | -0,216 | 0,1296 | ||
| -1,6 | 2,56 | -4,096 | 6,5536 | ||
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| -1,6 | 2,56 | -4,096 | 6,5536 | ||
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| 2,4 | 5,76 | 13,824 | 33,1776 | ||
| 0,4 | 0,16 | 0,064 | 0,0256 | ||
| -0,6 | 0,36 | -0,216 | 0,1296 | ||
| 2,6 | 24,36 | 23,944 | 88,2576 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 2,6
= 2,6
Стандартное отклонение вычисляется по формуле:
 = 1,10
= 1,10
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 0,85;
0,85;
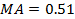 ;
;
 = 2,8;
= 2,8;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 22
Вычисление показателей асимметрии и эксцесса для 6 класса (показатели по методике «Несуществующее животное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -0,3 | 0,09 | -0,027 | 0,0081 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| -0,3 | 0,09 | -0,027 | 0,0081 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| -0,3 | 0,09 | -0,027 | 0,0081 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| 2,7 | 7,29 | 19,683 | 53,1441 | ||
| 0,7 | 0,49 | 0,343 | 0,2401 | ||
| 0,7 | 0,49 | 0,343 | 0,2401 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| 0,7 | 0,49 | 0,343 | 0,2401 | ||
| -0,3 | 0,09 | -0,027 | 0,0081 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| 1,7 | 2,89 | 4,913 | 8,3521 | ||
| -0,3 | 0,09 | -0,027 | 0,0081 | ||
| 1,7 | 2,89 | 4,913 | 8,3521 | ||
| 2,7 | 7,29 | 19,683 | 53,1441 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| -0,3 | 0,09 | -0,027 | 0,0081 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| 1,7 | 2,89 | 4,913 | 8,3521 | ||
| 1,3 | 37,09 | 39,593 | 152,1061 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 1,3
= 1,3
Стандартное отклонение вычисляется по формуле:
 = 1,3
= 1,3
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Дата добавления: 2015-10-30; просмотров: 145 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Результаты исследования 3 страница | | | Описание метода рангового коэффициента корреляции rs Спирмена |