Результаты исследования 1 страница

Первичные результаты исследования по методикам «Несуществующие животное», опросника «Уровень агрессивности» по А.Басса и А.Дарки (в адаптации А.К. Осницкого) и «Самооценка форм агрессивного поведения (модифицированный вариант Басса-Дарки)», опросник «Агрессивность» А.И Крупнова представлены в Приложении 4.

Проверка нормальности распределения результативного признака путем расчета показателей асимметрии и эксцесса и сопоставления их с критическими значениями по Плохинскому Н. А.

Таблица 1

Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике Басса-Дарки «Физическая агрессия»)

№	Xi	Xi-Xср	(Xi-Xср)2	(Xi-Xср)3	(Xi-Xср)4
		0,1304	0,017	0,00222	0,00028914
		22,1304	489,755	10838,5	239859,572
		-10,87	118,148	-1284,2	13958,9981
		-43,87	1924,54	-84429	3703861,16
		-10,87	118,148	-1284,2	13958,9981
		11,1304	123,886	1378,9	15347,6925
		22,1304	489,755	10838,5	239859,572
		-57,87	3348,89	-193799	11215068,3
		22,1304	489,755	10838,5	239859,572
		-32,87	1080,41	-35513	1167287,07
		11,1304	123,886	1378,9	15347,6925
		11,1304	123,886	1378,9	15347,7086
		0,1304	0,017	0,00222	0,00028914
		11,1304	123,886	1378,9	15347,7086
		11,1304	123,886	1378,9	15347,6925
		33,1304	1097,62	36364,7	1204777,14
		11,1304	123,886	1378,9	15347,6925
		22,1304	489,755	10838,5	239860,34
		11,1304	123,886	1378,9	15347,7
		-10,87	118,148	-1284,2	13958,9981
		11,1304	123,886	1378,9	15347,7
		-32,87	1080,41	-35513	1167287,07
		-10,87	118,148	-1284,2	13958,9577
Ср. Знач.	65,8696	Суммы:	11954,6	-263640	19596337,3

= ,

Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.

= = 65.86

Стандартное отклонение вычисляется по формуле:

= = 23,310

Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:

Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,

- стандартное отклонение.

В данном случае:

= -0,905;

;

-3 = 10,7;

;

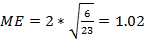Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:

;

.

В данном случае:

;

.

Мы видим что распределение данного признака далеко от нормального [18, 230-233].

Таблица 2

Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике Басса-Дарки «Косвенная агрессия»)

№	Xi	Xi-Xср	(Xi-Xср)2	(Xi-Xср)3	(Xi-Xср)4
		11,44	130,8736	1497,194	17127,899
		-1,56	2,4336	-3,79642	-9,238958
		-1,56	2,4336	-3,79642	-9,238958
		-40,56	1645,114	-66725,8	2706398,8
		-1,56	2,4336	-3,79642	-9,238958
		24,44	597,3136	14598,34	356783,54
		11,44	130,8736	1497,194	17127,899
		-1,56	2,4336	-3,79642	-9,238958
		-14,56	211,9936	-3086,63	44941,286
		11,44	130,8736	1497,194	17127,899
		24,44	597,3136	14598,34	356783,54
		11,44	130,8736	1497,194	17127,899
		24,44	597,3136	14598,34	356783,54
		11,44	130,8736	1497,194	17127,899
		-40,56	1645,114	-66725,8	2706398,8
		-4,56	20,7936	-94,8188	432,3738
		-14,56	211,9936	-3086,63	44941,286
		-14,56	211,9936	-3086,63	44941,286
		-14,56	211,9936	-3086,63	44941,286
		24,44	597,3136	14598,34	356783,54
		-14,56	211,9936	-3086,63	44941,286
		11,44	130,8736	1497,19	17127,854
		-1,56	2,4336	-3,79642	-9,238958
Ср. Зн.	66,56		7557,65	-81622

= ,

Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.

= 66.56

Стандартное отклонение вычисляется по формуле:

= 18,534

Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:

Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,

- стандартное отклонение.

В данном случае:

-5,57;

;

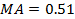= 6,75;

;

Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:

;

.

В данном случае:

;

.

Мы видим что распределение данного признака далеко от нормального [18, 230-233].

Таблица 3

Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике Басса-Дарки «Индекс агрессивности»)

№	Xi	Xi-Xср	(Xi-Xср)2	(Xi-Xср)3	(Xi-Xср)4
		-4,31	18,5761	-80,062991	345,0714912
	20,33	-35,98	1294,5604	-46578,2832	1675886,629
		-4,31	18,5761	-80,062991	345,0714912
		-24,31	590,9761	-14366,629	349252,7508
	58,6	2,29	5,2441	12,008989	27,50058481
		15,69	246,1761	3862,503009	60602,67221
	79,3	22,99	528,5401	12151,1369	279354,6373
	40,3	-160,1	25632,01	-4103684,8	656999936,6
	73,3	19,99	399,6001	7988,005999	159680,2399
	39,6	-17		-4913
		23,69	561,2161	13295,20941	314963,5109
		16,69	278,5561	4649,101309	68295,29823
		14,69	215,7961	3170,044709	46567,95678
	66,6	10,29	105,8841	1089,547389	11211,44263
	50,3	-6,01	36,1201	-217,081801	1304,661624
	38,3	-18,01	324,3601	-5841,7254	105209,4745
	38,3	-18,01	324,3601	-5841,7254	105209,4745
	78,6	22,29	496,8441	11074,65499	246854,0597
		2,69	7,2361	19,465109	52,36114321
		13,69	187,4161	2565,726409	35124,79454
		2,69	7,2361	19,465109	52,36114321
	39,6	-16,71	279,2241	-4665,83471	77966,09802
		-4,31	18,5761	-80,062991	345,0714912
Ср. зн.	56,31	-141,38	31866,084	-4126452,4

= ,

Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.

= 56.31

Стандартное отклонение вычисляется по формуле:

= 38

Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:

Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,

- стандартное отклонение.

В данном случае:

-2,2;

;

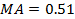= -1,6;

;

Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:

;

.

В данном случае:

;

.

Мы видим что распределение данного признака далеко от нормального [18, 230-233].

Таблица 4

Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике «Несуществующее животное»)

№	Xi	Xi-Xср	(Xi-Xср)2	(Xi-Xср)3	(Xi-Xср)4
		-9,6	92,16	-884,736	8493,4656
		-11,6	134,56	-1560,9	18106,3936
		-12,6	158,76	-2000,38	25204,7376
		-10,6	112,36	-1191,02	12624,7696
		-12,6	158,76	-2000,38	25204,7376
		-11,6	134,56	-1560,9	18106,3936
		-12,6	158,76	-2000,38	25204,7376
		-12,6	158,76	-2000,38	25204,7376
		-10,6	112,36	-1191,02	12624,7696
		-12,6	158,76	-2000,38	25204,7376
		-13,6	184,96	-2515,46	34210,2016
		-9,6	92,16	-884,736	8493,4656
		-11,6	134,56	-1560,9	18106,3936
		-11,6	134,56	-1560,9	18106,3936
		-10,6	112,36	-1191,02	12624,7696
		-12,6	158,76	-2000,38	25204,7376
		-10,6	112,36	-1191,02	12624,7696
		-13,6	184,96	-2515,46	34210,2016
		-10,6	112,36	-1191,02	12624,7696
		-13,6	184,96	-2515,46	34210,2016
		-11,6	134,56	-1560,9	18106,3936
		-13,6	184,96	-2515,46	34210,2016
		-11,6	134,56	-1560,9	18106,3936
Ср. зн.	13,6		3245,88	-39154	476818,373

= ,

Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.

= 13,6

Стандартное отклонение вычисляется по формуле:

= -3,8

Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:

Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,

- стандартное отклонение.

В данном случае:

-31;

;

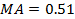= 96;

;

Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:

;

.

В данном случае:

;

.

Мы видим что распределение данного признака далеко от нормального [18, 230-233].

Таблица 5

Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике «Агрессивность» И.А.Крупнов, «4 четное»)

№	Xi	Xi-Xср	(Xi-Xср)2	(Xi-Xср)3	(Xi-Xср)4
		6,1	37,21	226,981	1384,5841
		8,1	65,61	531,441	4304,6721
		-3,9	15,21	-59,319	231,3441
		-13,9	193,21	-2685,62	37330,104
		-15,9	252,81	-4019,68	63912,896
		12,1	146,41	1771,561	21435,888
		15,1	228,01	3442,951	51988,56
		-5,9	34,81	-205,379	1211,7361
		5,1	26,01	132,651	676,5201
		4,1	16,81	68,921	282,5761
		2,1	4,41	9,261	19,4481
		8,1	65,61	531,441	4304,6721
		-9,9	98,01	-970,299	9605,9601
		1,1	1,21	1,331	1,4641
		-0,9	0,81	-0,729	0,6561
		5,1	26,01	132,651	676,5201
		-10,9	118,81	-1295,03	14115,816
		4,1	16,81	68,921	282,5761
		0,1	0,01	0,001	0,0001
		-5,9	34,81	-205,379	1211,7361
		-3,9	15,21	-59,319	231,3441
		4,1	16,81	68,921	282,5761
		-3,9	15,21	-59,319	231,3441
Ср. зн.	19,9		1429,83	-2573,04	213722,99

= ,

Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.

= 19,9

Стандартное отклонение вычисляется по формуле:

= 8,06

Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:

Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,

- стандартное отклонение.

В данном случае:

-0,213;

;

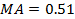= -0,79;

;

Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:

;

.

В данном случае:

;

.

Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].

Таблица 6

Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике «Агрессивность» И.А.Крупнов, «4 нечетное»)

№	Xi	Xi-Xср	(Xi-Xср)2	(Xi-Xср)3	(Xi-Xср)4
		-0,2	0,04	-0,008	0,0016
		8,8	77,44	681,472	5996,9536
		6,8	46,24	314,432	2138,1376
		-11,2	125,44	-1404,928	15735,1936
		-9,2	84,64	-778,688	7163,9296
		8,8	77,44	681,472	5996,9536
		8,8	77,44	681,472	5996,9536
		-7,2	51,84	-373,248	2687,3856
		6,2	38,44	238,328	1477,6336
		2,8	7,84	21,952	61,4656
		9,8	96,04	941,192	9223,6816
		7,8	60,84	474,552	3701,5056
		-11,2	125,44	-1404,928	15735,1936
		4,8	23,04	110,592	530,8416
		-4,2	17,64	-74,088	311,1696
		2,8	7,84	21,952	61,4656
		-11,2	125,44	-1404,928	15735,1936
		-3,2	10,24	-32,768	104,8576
		9,8	96,04	941,192	9223,6816
		-12,2	148,84	-1815,848	22153,3456
		-0,2	0,04	-0,008	0,0016
		2,8	7,84	21,952	61,4656
		4,8	23,04	110,592	530,8416
Ср. зн	19,2		1329,12	-2048,288	124627,8528

= ,

Дата добавления: 2015-10-30