
Читайте также:
|
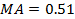 ;
;
 = 1,9;
= 1,9;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
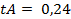 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 12
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике «Несуществующее животное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| 1,1 | 1,21 | 1,331 | 1,4641 | ||
| 1,1 | 1,21 | 1,331 | 1,4641 | ||
| 1,1 | 1,21 | 1,331 | 1,4641 | ||
| -1,9 | 3,61 | -6,859 | 13,0321 | ||
| -0,9 | 0,81 | -0,729 | 0,6561 | ||
| 2,1 | 4,41 | 9,261 | 19,4481 | ||
| -1,9 | 3,61 | -6,859 | 13,0321 | ||
| 1,1 | 1,21 | 1,331 | 1,4641 | ||
| -0,9 | 0,81 | -0,729 | 0,6561 | ||
| 1,1 | 1,21 | 1,331 | 1,4641 | ||
| -0,9 | 0,81 | -0,729 | 0,6561 | ||
| 0,1 | 0,01 | 0,001 | 0,0001 | ||
| 1,1 | 1,21 | 1,331 | 1,4641 | ||
| 0,1 | 0,01 | 0,001 | 0,0001 | ||
| 1,1 | 1,21 | 1,331 | 1,4641 | ||
| 2,1 | 4,41 | 9,261 | 19,4481 | ||
| -0,9 | 0,81 | -0,729 | 0,6561 | ||
| -1,9 | 3,61 | -6,859 | 13,0321 | ||
| 0,1 | 0,01 | 0,001 | 0,0001 | ||
| 2,1 | 4,41 | 9,261 | 19,4481 | ||
| -0,9 | 0,81 | -0,729 | 0,6561 | ||
| -1,9 | 3,61 | -6,859 | 13,0321 | ||
| -0,9 | 0,81 | -0,729 | 0,6561 | ||
| -0,9 | 0,81 | -0,729 | 0,6561 | ||
| ср зн | 1,9 | сумма: | 41,84 | 4,564 | 125,3144 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 1,9
= 1,9
Стандартное отклонение вычисляется по формуле:
 = 1,3
= 1,3
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 0,08;
0,08;
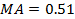 ;
;
 = -1,17;
= -1,17;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
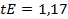 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 13
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике «Агрессивность» И.А.Крупнов, «4 четное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -10,3 | 106,09 | -1092,73 | 11255,0881 | ||
| 4,7 | 22,09 | 103,823 | 487,9681 | ||
| -14,3 | 204,49 | -2924,21 | 41816,1601 | ||
| 20,7 | 428,49 | 8869,743 | 183603,6801 | ||
| 2,7 | 7,29 | 19,683 | 53,1441 | ||
| 0,7 | 0,49 | 0,343 | 0,2401 | ||
| -13,3 | 176,89 | -2352,64 | 31290,0721 | ||
| 15,7 | 246,49 | 3869,893 | 60757,3201 | ||
| 5,7 | 32,49 | 185,193 | 1055,6001 | ||
| -6,3 | 39,69 | -250,047 | 1575,2961 | ||
| -7,3 | 53,29 | -389,017 | 2839,8241 | ||
| -4,3 | 18,49 | -79,507 | 341,8801 | ||
| 14,7 | 216,09 | 3176,523 | 46694,8881 | ||
| -2,3 | 5,29 | -12,167 | 27,9841 | ||
| 7,7 | 59,29 | 456,533 | 3515,3041 | ||
| -6,3 | 39,69 | -250,047 | 1575,2961 | ||
| 3,7 | 13,69 | 50,653 | 187,4161 | ||
| -3,3 | 10,89 | -35,937 | 118,5921 | ||
| -20 | -8000 | ||||
| 3,7 | 13,69 | 50,653 | 187,4161 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| -7,3 | 53,29 | -389,017 | 2839,8241 | ||
| 6,7 | 44,89 | 300,763 | 2015,1121 | ||
| 11,7 | 136,89 | 1601,613 | 18738,8721 | ||
| Ср. зн. | 24,3 | 2331,67 | 2907,909 | 570979,8343 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 24,3
= 24,3
Стандартное отклонение вычисляется по формуле:
 = 10
= 10
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 1,2;
1,2;
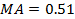 ;
;
 = -0,6;
= -0,6;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
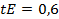 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 14
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике «Агрессивность» И.А.Крупнов, «4 нечетное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -4,7 | 22,09 | -103,823 | 487,9681 | ||
| -2,7 | 7,29 | -19,683 | 53,1441 | ||
| -10,7 | 114,49 | -1225,04 | 13107,96 | ||
| 11,3 | 127,69 | 1442,897 | 16304,74 | ||
| 3,3 | 10,89 | 35,937 | 118,5921 | ||
| -4,7 | 22,09 | -103,823 | 487,9681 | ||
| 2,3 | 5,29 | 12,167 | 27,9841 | ||
| -5,7 | 32,49 | -185,193 | 1055,6 | ||
| -2,7 | 7,29 | -19,683 | 53,1441 | ||
| -9,7 | 94,09 | -912,673 | 8852,928 | ||
| -12,7 | 161,29 | -2048,38 | 26014,46 | ||
| -2,7 | 7,29 | -19,683 | 53,1441 | ||
| 16,3 | 265,69 | 4330,747 | 70591,18 | ||
| 7,3 | 53,29 | 389,017 | 2839,824 | ||
| 13,3 | 176,89 | 2352,637 | 31290,07 | ||
| -3,7 | 13,69 | -50,653 | 187,4161 | ||
| 2,3 | 5,29 | 12,167 | 27,9841 | ||
| -10,7 | 114,49 | -1225,04 | 13107,96 | ||
| -12,7 | 161,29 | -2048,38 | 26014,46 | ||
| 10,3 | 106,09 | 1092,727 | 11255,09 | ||
| 0,3 | 0,09 | 0,027 | 0,0081 | ||
| -0,7 | 0,49 | -0,343 | 0,2401 | ||
| 7,3 | 53,29 | 389,017 | 2839,824 | ||
| 10,3 | 106,09 | 1092,727 | 11255,09 | ||
| Ср зн | 26,7 | 1668,96 | 3187,658 | 236026,8 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 26,7
= 26,7
Стандартное отклонение вычисляется по формуле:
 = 8,5
= 8,5
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 0,21;
0,21;
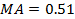 ;
;
 = -1,1;
= -1,1;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
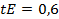 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 15
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике «Агрессивность» И.А.Крупнов, «5 четное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| 2,8 | 7,84 | 21,952 | 61,4656 | ||
| 3,8 | 14,44 | 54,872 | 208,5136 | ||
| -1,2 | 1,44 | -1,728 | 2,0736 | ||
| 15,8 | 249,64 | 3944,312 | 62320,1296 | ||
| 2,8 | 7,84 | 21,952 | 61,4656 | ||
| 2,8 | 7,84 | 21,952 | 61,4656 | ||
| -5,2 | 27,04 | -140,608 | 731,1616 | ||
| -10,2 | 104,04 | -1061,208 | 10824,3216 | ||
| 5,8 | 33,64 | 195,112 | 1131,6496 | ||
| -17,2 | 295,84 | -5088,448 | 87521,3056 | ||
| -17,2 | 295,84 | -5088,448 | 87521,3056 | ||
| -11,2 | 125,44 | -1404,928 | 15735,1936 | ||
| 14,8 | 219,04 | 3241,792 | 47978,5216 | ||
| 5,8 | 33,64 | 195,112 | 1131,6496 | ||
| 9,8 | 96,04 | 941,192 | 9223,6816 | ||
| 2,8 | 7,84 | 21,952 | 61,4656 | ||
| 15,8 | 249,64 | 3944,312 | 62320,1296 | ||
| -5,2 | 27,04 | -140,608 | 731,1616 | ||
| -13,2 | 174,24 | -2299,968 | 30359,5776 | ||
| -2,2 | 4,84 | -10,648 | 23,4256 | ||
| -8,2 | 67,24 | -551,368 | 4521,2176 | ||
| -10,2 | 104,04 | -1061,208 | 10824,3216 | ||
| 10,8 | 116,64 | 1259,712 | 13604,8896 | ||
| 9,8 | 96,04 | 941,192 | 9223,6816 | ||
| Ср.зн. | 25,2 | 2367,16 | -2043,752 | 456183,7744 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 25,2
= 25,2
Стандартное отклонение вычисляется по формуле:
 = 10,1
= 10,1
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,08;
-0,08;
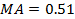 ;
;
 = -1,1;
= -1,1;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 16
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике «Агрессивность» И.А.Крупнов, «5 нечетное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| 1,5 | 2,25 | 3,375 | 5,0625 | ||
| 13,5 | 182,25 | 2460,375 | 33215,06 | ||
| 1,5 | 2,25 | 3,375 | 5,0625 | ||
| 17,5 | 306,25 | 5359,375 | 93789,06 | ||
| 3,5 | 12,25 | 42,875 | 150,0625 | ||
| 2,5 | 6,25 | 15,625 | 39,0625 | ||
| -0,5 | 0,25 | -0,125 | 0,0625 | ||
| -14,5 | 210,25 | -3048,63 | 44205,06 | ||
| -2,5 | 6,25 | -15,625 | 39,0625 | ||
| -18,5 | 342,25 | -6331,63 | 117135,1 | ||
| -0,5 | 0,25 | -0,125 | 0,0625 | ||
| -13,5 | 182,25 | -2460,38 | 33215,06 | ||
| 8,5 | 72,25 | 614,125 | 5220,063 | ||
| 5,5 | 30,25 | 166,375 | 915,0625 | ||
| 4,5 | 20,25 | 91,125 | 410,0625 | ||
| -2,5 | 6,25 | -15,625 | 39,0625 | ||
| 12,5 | 156,25 | 1953,125 | 24414,06 | ||
| -1,5 | 2,25 | -3,375 | 5,0625 | ||
| -12,5 | 156,25 | -1953,13 | 24414,06 | ||
| 7,5 | 56,25 | 421,875 | 3164,063 | ||
| -4,5 | 20,25 | -91,125 | 410,0625 | ||
| -20,5 | 420,25 | -8615,13 | 176610,1 | ||
| 11,5 | 132,25 | 1520,875 | 17490,06 | ||
| 6,5 | 42,25 | 274,625 | 1785,063 | ||
| 26,5 | -9607,75 | 576674,5 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 26,5
= 26,5
Стандартное отклонение вычисляется по формуле:
 = 10,1
= 10,1
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,38;
-0,38;
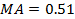 ;
;
 = -0,6;
= -0,6;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
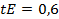 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 17
Вычисление показателей асимметрии и эксцесса для 6 класса (показатели по методике Басса-Дарки «Физическая агрессия»)
Дата добавления: 2015-10-30; просмотров: 121 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Результаты исследования 2 страница | | | Результаты исследования 4 страница |