
Читайте также:
|
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 19,2
= 19,2
Стандартное отклонение вычисляется по формуле:
 = 7,7
= 7,7
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,19;
-0,19;
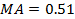 ;
;
 = -1,4;
= -1,4;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 7
Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике «Агрессивность» И.А.Крупнов, «5 четное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -20 | -8000 | ||||
| -6,8 | 46,24 | -314,432 | 2138,138 | ||
| -11,8 | 139,24 | -1643,03 | 19387,78 | ||
| -16,5 | 272,25 | -4492,13 | 74120,06 | ||
| -20 | -8000 | ||||
| 12,2 | 148,84 | 1815,848 | 22153,35 | ||
| 9,2 | 84,64 | 778,688 | 7163,93 | ||
| -0,8 | 0,64 | -0,512 | 0,4096 | ||
| 4,2 | 17,64 | 74,088 | 311,1696 | ||
| 7,2 | 51,84 | 373,248 | 2687,386 | ||
| 4,2 | 17,64 | 74,088 | 311,1696 | ||
| 8,2 | 67,24 | 551,368 | 4521,218 | ||
| -11,8 | 139,24 | -1643,03 | 19387,78 | ||
| -2,8 | 7,84 | -21,952 | 61,4656 | ||
| -2,8 | 7,84 | -21,952 | 61,4656 | ||
| 10,2 | 104,04 | 1061,208 | 10824,32 | ||
| 2,2 | 4,84 | 10,648 | 23,4256 | ||
| 14,2 | 201,64 | 2863,288 | 40658,69 | ||
| 10,2 | 104,04 | 1061,208 | 10824,32 | ||
| 14,2 | 201,64 | 2863,288 | 40658,69 | ||
| 10,2 | 104,04 | 1061,208 | 10824,32 | ||
| 7,2 | 51,84 | 373,248 | 2687,386 | ||
| -11,8 | 139,24 | -1643,03 | 19387,78 | ||
| ср зн | 20,8 | 2712,45 | -12818,6 | 608194,2 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 20,8
= 20,8
Стандартное отклонение вычисляется по формуле:
 = 11,10
= 11,10
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,4;
-0,4;
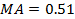 ;
;
 = 37;
= 37;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
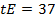 .
.
Мы видим что распределение данного признака далеко от нормального [18, 230-233].
Таблица 8
Вычисление показателей асимметрии и эксцесса для 11 класса (показатели по методике «Агрессивность» И.А.Крупнов, «5 нечетное»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -10,5 | 110,25 | -1157,63 | 12155,06 | ||
| -6,5 | 42,25 | -274,625 | 1785,063 | ||
| -5,5 | 30,25 | -166,375 | 915,0625 | ||
| -19,5 | 380,25 | -7414,88 | 144590,1 | ||
| -9,5 | 90,25 | -857,375 | 8145,063 | ||
| 8,5 | 72,25 | 614,125 | 5220,063 | ||
| 6,5 | 42,25 | 274,625 | 1785,063 | ||
| 4,5 | 20,25 | 91,125 | 410,0625 | ||
| 5,5 | 30,25 | 166,375 | 915,0625 | ||
| 5,5 | 30,25 | 166,375 | 915,0625 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| 10,5 | 110,25 | 1157,625 | 12155,06 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| 2,5 | 6,25 | 15,625 | 39,0625 | ||
| -11,5 | 132,25 | -1520,88 | 17490,06 | ||
| -11,5 | 132,25 | -1520,88 | 17490,06 | ||
| 0,5 | 0,25 | 0,125 | 0,0625 | ||
| 15,5 | 240,25 | 3723,875 | 57720,06 | ||
| 13,5 | 182,25 | 2460,375 | 33215,06 | ||
| -11,5 | 132,25 | -1520,88 | 17490,06 | ||
| 13,5 | 182,25 | 2460,375 | 33215,06 | ||
| 5,5 | 30,25 | 166,375 | 915,0625 | ||
| -5,5 | 30,25 | -166,375 | 915,0625 | ||
| Ср. зн. | 19,5 | 2027,75 | -3302,63 | 367480,4 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 19,5
= 19,5
Стандартное отклонение вычисляется по формуле:
 = 9,6
= 9,6
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,16;
-0,16;
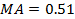 ;
;
 = -1,1;
= -1,1;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 9
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике Басса-Дарки «Физическая агрессия»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -19,9 | 396,01 | -7880,6 | 156823,9201 | ||
| 2,71 | 7,3441 | 19,90251 | 53,93580481 | ||
| 13,71 | 187,9641 | 2576,988 | 35330,50289 | ||
| -19,9 | 396,01 | -7880,6 | 156823,9201 | ||
| -8,29 | 68,7241 | -569,723 | 4723,001921 | ||
| 47,71 | 2276,244 | 108599,6 | 5181287,203 | ||
| -19,9 | 396,01 | -7880,6 | 156823,9201 | ||
| 13,71 | 187,9641 | 2576,988 | 35330,50289 | ||
| -30,29 | 917,4841 | -27790,6 | 841777,0738 | ||
| 2,71 | 7,3441 | 19,90251 | 53,93580481 | ||
| -19,9 | 396,01 | -7880,6 | 156823,9201 | ||
| -8,29 | 68,7241 | -569,723 | 4723,001921 | ||
| -19,9 | 396,01 | -7880,6 | 156823,9201 | ||
| -8,29 | 68,7241 | -569,723 | 4723,001921 | ||
| 13,71 | 187,9641 | 2576,988 | 35330,50289 | ||
| -8,29 | 68,7241 | -569,723 | 4723,001921 | ||
| 24,71 | 610,5841 | 15087,53 | 372812,9432 | ||
| 13,71 | 187,9641 | 2576,988 | 35330,50289 | ||
| 13,71 | 187,9641 | 2576,988 | 35330,50289 | ||
| -19,9 | 396,01 | -7880,6 | 156823,9201 | ||
| -8,29 | 68,7241 | -569,723 | 4723,001921 | ||
| 24,71 | 610,5841 | 15087,53 | 372812,9432 | ||
| 2,71 | 7,3441 | 19,90251 | 53,93580481 | ||
| 13,71 | 187,9641 | 2576,988 | 35330,50289 | ||
| ср знач | 63,29 | 8284,394 | 76373,51 | 7945393,518 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 63,29
= 63,29
Стандартное отклонение вычисляется по формуле:
 = 18,9
= 18,9
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 0,45;
0,45;
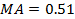 ;
;
 = 22,80;
= 22,80;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что распределение данного признака далеко от нормального [18, 230-233].
Таблица 10
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике Басса-Дарки «Косвенная агрессия»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| -14,3 | 204,49 | -2924,21 | 41816,16 | ||
| 37,7 | 1421,29 | 53582,63 | |||
| -24,3 | 590,49 | -14348,9 | 348678,4 | ||
| -14,3 | 204,49 | -2924,21 | 41816,16 | ||
| -14,3 | 204,49 | -2924,21 | 41816,16 | ||
| -14,3 | 204,49 | -2924,21 | 41816,16 | ||
| -27,3 | 745,29 | -20346,4 | 555457,2 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| 11,7 | 136,89 | 1601,613 | 18738,87 | ||
| -14,3 | 204,49 | -2924,21 | 41816,16 | ||
| 11,7 | 136,89 | 1601,613 | 18738,87 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| -27,3 | 745,29 | -20346,4 | 555457,2 | ||
| 24,7 | 610,09 | 15069,22 | 372209,8 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| 11,7 | 136,89 | 1601,613 | 18738,87 | ||
| 24,7 | 610,09 | 15069,22 | 372209,8 | ||
| 11,7 | 136,89 | 1601,613 | 18738,87 | ||
| -1,3 | 1,69 | -2,197 | 2,8561 | ||
| 27,7 | 767,29 | 21253,93 | 588733,9 | ||
| 24,7 | 610,09 | 15069,22 | 372209,8 | ||
| -40,3 | 1624,09 | -65450,8 | |||
| 11,7 | 136,89 | 1601,613 | 18738,87 | ||
| Ср зн | 66,3 | 9439,36 | -7072,29 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 66,3
= 66,3
Стандартное отклонение вычисляется по формуле:
 = 20,25
= 20,25
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,03;
-0,03;
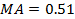 ;
;
 = -0,9;
= -0,9;
 ;
;
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
 ;
;
 .
.
В данном случае:
 ;
;
 .
.
Мы видим что оба показателя не превышают в 3 раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального [18, 230-233].
Таблица 11
Вычисление показателей асимметрии и эксцесса для 10 класса (показатели по методике Басса-Дарки «Индекс агрессивности»)
| № | Xi | Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 |
| 34,66 | -24,68 | 609,1024 | -15032,647 | 371005,7337 | |
| 83,3 | 23,96 | 574,0816 | 13754,9951 | 329569,6835 | |
| 50,3 | -9,04 | 81,7216 | -738,76326 | 6678,419907 | |
| 50,6 | -8,74 | 76,3876 | -667,62762 | 5835,065434 | |
| -2,34 | 5,4756 | -12,812904 | 29,98219536 | ||
| 78,3 | 18,86 | 355,6996 | 6708,49446 | 126522,2054 | |
| -18,34 | 336,3556 | -6168,7617 | 113135,0897 | ||
| 71,3 | 11,96 | 143,0416 | 1710,77754 | 20460,89933 | |
| 43,3 | -16,04 | 257,2816 | -4126,7969 | 66193,8217 | |
| 61,3 | 1,96 | 3,8416 | 7,529536 | 14,75789056 | |
| -11,34 | 128,5956 | -1458,2741 | 16536,82834 | ||
| 59,3 | -0,04 | 0,0016 | -0,000064 | 0,00000256 | |
| 49,6 | -9,74 | 94,8676 | -924,01042 | 8999,86153 | |
| -9,34 | 87,2356 | -814,7805 | 7610,049907 | ||
| 74,6 | 15,26 | 232,8676 | 3553,55958 | 54227,31913 | |
| 53,3 | -6,04 | 36,4816 | -220,34886 | 1330,907139 | |
| 14,66 | 214,9156 | 3150,6627 | 46188,71512 | ||
| 74,6 | 15,26 | 232,8676 | 3553,55958 | 54227,31913 | |
| 78,3 | 18,96 | 359,4816 | 6815,77114 | 129227,0207 | |
| 60,3 | 0,96 | 0,9216 | 0,884736 | 0,84934656 | |
| 60,3 | 0,96 | 0,9216 | 0,884736 | 0,84934656 | |
| 74,6 | 15,26 | 232,8676 | 3553,55958 | 54227,31913 | |
| 31,3 | -28,04 | 786,2416 | -22046,214 | 618175,8536 | |
| 5,66 | 32,0356 | 181,321496 | 1026,279667 | ||
| ср зн | 59,34 | 4883,291 | -9219,038 | 2031224,8 |
 =
=  ,
,
Где Xi – каждое наблюдаемое значение признака; n – количество наблюдений.
 = 59,34
= 59,34
Стандартное отклонение вычисляется по формуле:
 = 14,5
= 14,5
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:




Где (Xi-Xсред.) – стандартное отклонение, n – количество испытуемых,
 - стандартное отклонение.
- стандартное отклонение.
В данном случае:
 -0,12;
-0,12;
Дата добавления: 2015-10-30; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Результаты исследования 1 страница | | | Результаты исследования 3 страница |