Solution to Integrative problem. 1. Holding-period returns for market, Reynolds Computer, and Andrews

1. Holding-period returns for Market, Reynolds Computer, and Andrews

Market Reynolds Computer Andrews

Price kt (kt- )² Price kt (kt- )² Price kt (kt- )²

	May	1090.82				20.60				24.00
	June	1133.84	3.94%	0.0007		23.20	12.62%	0.0067		26.72	11.33%	0.0065
	July	1120.67	-1.16%	0.0006		27.15	17.03%	0.0158		20.94	-21.63%	0.0619
	Aug	957.28	-14.58%	0.0251		25.00	-7.92%	0.0153		15.78	-24.64%	0.0778
	Sept	1017.01	6.24%	0.0025		32.88	31.52%	0.0733		18.09	14.64%	0.0130
	Oct	1098.67	8.03%	0.0046		32.75	-0.40%	0.0023		21.69	19.90%	0.0277
	Nov	1163.63	5.91%	0.0022		30.41	-7.15%	0.0134		23.06	6.32%	0.0009
	Dec	1229.23	5.64%	0.0019		36.59	20.32%	0.0252		28.06	21.68%	0.0340
	Jan	1279.64	4.10%	0.0008		50.00	36.65%	0.1037		26.03	-7.23%	0.0110
	Feb	1238.33	-3.23%	0.0020		40.06	-19.88%	0.0592		26.44	1.58%	0.0003
	Mar	1286.37	3.88%	0.0007		40.88	2.05%	0.0006		28.06	6.13%	0.0008
	Apr	1335.18	3.79%	0.0006		41.19	0.76%	0.0014		36.94	31.65%	0.0806
	May	1301.84	-2.50%	0.0014		34.44	-16.39%	0.0434		36.88	-0.16%	0.0012
	June	1372.71	5.44%	0.0018		37.00	7.43%	0.0009		37.56	1.84%	0.0002
	July	1328.72	-3.20%	0.0020		40.88	10.49%	0.0037		23.25	-38.10%	0.1710
	Aug	1320.41	-0.63%	0.0004		48.81	19.40%	0.0224		22.88	-1.59%	0.0023
	Sept	1282.71	-2.86%	0.0017		41.81	-14.34%	0.0353		24.78	8.30%	0.0026
	Oct	1362.93	6.25%	0.0025		40.13	-4.02%	0.0072		27.19	9.73%	0.0042
	Nov	1388.91	1.91%	0.0000		43.00	7.15%	0.0007		26.56	-2.32%	0.0031
	Dec	1469.25	5.78%	0.0021		51.00	18.60%	0.0201		24.25	-8.70%	0.0143
	Jan	1394.46	-5.09%	0.0040		38.44	-24.63%	0.0845		32.00	31.96%	0.0824
	Febr	1366.42	-2.01%	0.0011		40.81	6.17%	0.0003		35.13	9.78%	0.0043
	Mar	1498.58	9.67%	0.0071		53.94	32.17%	0.0769		44.81	27.55%	0.0591
	Apr	1452.43	-3.08%	0.0019		50.13	-7.06%	0.0132		30.23	-32.54%	0.1281
	May	1420.60	-2.19%	0.0012		43.13	-13.96%	0.0339		34.00	12.47%	0.0085
	Sum		30.07%	.0689			106.62%				77.95%	.7958

2. Average

Monthly

Return 1.25% 4.44% 3.25%

Standard

Deviation 5.47% 16.93% 18.60%

3.

4 Reynolds’s returns have a great amount of volatility with some correlation to the market returns.

The same can be said of Andrews. The returns show a great amount of volatility that followed the market returns only part of the time.

5. Monthly returns of a portfolio of equal amounts of Reynolds and Andrews.

Monthly

Returns

	June	11.98%
	July	-2.32%
	August	-16.27%
	September	23.08%
	October	9.74%
	November	-0.41%
	December	21.02%
	January	14.70%
	February	-9.16%
	March	4.09%
	April	16.20%
	May	-8.28%
	June	4.65%
	July	-13.81%
	August	8.90%
	September	-3.00%
	October	2.84%
	November	2.43%
	December	4.95%
	January	3.66%
	February	7.97%
	March	29.87%
	April	-19.80%
	May	-0.75%
	Average return	3.84%
	Standard deviation	12.29%

6.

We see in this new graph where both stocks are included as a single portfolio that the relationship of the stocks with the market approximates an average of the relationships taken alone. Note the reduction in volatility that occurs when risk is diversified even between just two stocks.

7. Monthly holding-period returns for long-term government bonds

(ki- )²

	June	5.70%	0.48%	0.000000%
	July	5.68%	0.47%	0.000001%
	August	5.54%	0.46%	0.000004%
	September	5.20%	0.43%	0.000023%
	October	5.01%	0.42%	0.000041%
	November	5.25%	0.44%	0.000020%
	December	5.06%	0.42%	0.000036%
	January	5.16%	0.43%	0.000027%
	February	5.37%	0.45%	0.000012%
	March	5.58%	0.47%	0.000003%
	April	5.55%	0.46%	0.000004%
	May	5.81%	0.48%	0.000000%
	June	6.04%	0.50%	0.000005%
	July	5.98%	0.50%	0.000003%
	August	6.07%	0.51%	0.000006%
	September	6.07%	0.51%	0.000006%
	October	6.26%	0.52%	0.000016%
	November	6.15%	0.51%	0.000009%
	December	6.35%	0.53%	0.000022%
	January	6.63%	0.55%	0.000050%
	February	6.23%	0.52%	0.000014%
	March	6.05%	0.50%	0.000005%
	April	5.85%	0.49%	0.000000%
	May	6.15%	0.51%	0.000009%

Average

Monthly

Return 0.48%

Standard

Deviation 0.04%

8. Monthly portfolio returns when portfolio consists of equal amounts invested in Reynolds, Andrews, and long-term government bonds.

(ki- )²

	June	8.14%	0.0029
	July	-1.39%	0.0017
	August	-10.69%	0.0180
	September	15.53%	0.0164
	October	6.63%	0.0015
	November	-0.13%	0.0008
	December	14.15%	0.0131
	January	9.94%	0.0052
	February	-5.95%	0.0075
	March	2.88%	0.0000
	April	10.95%	0.0068
	May	-5.36%	0.0065
	June	3.27%	0.0000
	July	-9.04%	0.0138
	August	6.10%	0.0011
	September	-1.83%	0.0021
	October	2.07%	0.0000
	November	1.79%	0.0001
	December	3.48%	0.0001
	January	2.63%	0.0000
	February	5.49%	0.0008
	March	20.08%	0.0301
	April	-13.04%	0.0248
	May	-0.33%	0.0009
	Sum	65.36%	0.1542

2.72%

Std. Dev.. 8.19%

9. Comparison of average returns and standard deviations

Average Standard

Returns Deviations

Reynolds 4.44% 16.93%

Andrews 3.25% 18.60%

Government security 0.48% 0.04%

Reynolds & Andrews 3.84% 12.29%

Reynolds, Andrews, 2.72% 8.19%

& government security

Market 1.25% 5.47%

From the findings above, we see that higher average returns are associated with higher risk (standard deviations), and that by diversification we can reduce risk, possibly without reducing the average return.

10. Based on the standard deviations, Andrews has more risk than Reynolds, 18.60 percent standard deviation versus 16.93 percent standard deviation. However, when we only consider systematic risk, Andrews is slightly less risky--Reynolds's beta is 1.96 compared to Andrews’ beta of 1.49. (The betas given here for Reynolds and Andrews come from financial services who calculate firms' betas. These are not consistent with the graphs above where we see Andrews' returns as being more responsive to the general market. We are seeing the problem of using only 24 months of returns as we have done.)

11. = + (Market Return - Risk-Free Rate) X Beta

Market Return = 1.25 % Average Monthly Return X 12 Months = 15%.

(The average returns for the market over a two-year period may be high or low relative to the longer-term past, and as a result should not be considered as “typical” investor expectations. For instance, if we used information from Ibbotson & Sinquefield for the years 1926-2002, the market risk premium—market return less risk-free rate—was 8.4 percent, and not the 19 percent that we use below. The point: Do not think two years fairly captures what we can expect in the future?)

Reynolds:

23.64% = 6% + (15% - 6%) X 1.96

Andrews:

19.41% = 6% + (15% - 6%) X 1.49

And if we used the market premium of 8.4 percent:

Reynolds:

22.46% = 6% + 8.4% X 1.96

Andrews:

18.52% = 6% + 8.4% X 1.49

Solutions to Problem Set B

6-1B.

k_rf =.05 +.07 + (.05 x.07)

k_rf =.1235

or

12.35% = nominal rate of interest

6-2B.

k_rf =.03 +.05 + (.03 x.05)

k_rf =.0815

or

8.15% = nominal rate of interest

6-3B.

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

.15 -3% -0.45% 4.788

.30 2 0.60 0.127

.40 4 1.60 0.729

.15 6 0.901.683

= 2.65% s² = 7.327%

s = 2.707%

No, Gautney should not invest in the security. The security’s expected rate of return is less than the rate offered on treasury bills.

6-4B.

Security A:

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

0.2 - 2% -0.4% 69.19%

0.5 19 9.5 2.88

0.3 25 7.521.17

= 16.6% s² = 93.24%

s = 9.66%

Security B:

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

0.1 5% 0.5% 2.704%

0.3 7 2.1 3.072

0.4 12 4.8 1.296

0.2 14 2.82.888

= 10.2% s² = 9.96%

s = 3.16%

Security ASecurity B

= 16.6% = 10.2%

s = 9.66% s = 3.16%

We cannot say which investment is "better." It would depend on the investor's attitude toward the risk-return tradeoff.

6-5B.

Common Stock A:

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

0.2 10% 2.0% 2.89%

0.6 13 7.8 0.38

0.2 20 4.07.69

= 13.8% s² = 10.96%

s = 3.31%

Common Stock B

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

0.15 6% 0.9% 5.67%

0.30 8 2.4 5.17

0.40 15 6.0 3.25

0.15 19 2.857.04

= 12.15% s² = 21.13%

s = 4.60%

Common Stock A is better. It has a higher expected return with less risk.

6-6B.

(a) = + Beta

= 8 % + 1.5 (16% - 8%)

= 20%

(b) The 20 percent "fair rate" compensates the investor for the time value of money and for assuming risk. However, only nondiversifiable risk is being considered, which is appropriate.

6-7B. Eye balling the characteristic line for the problem, the rise relative to the run is about 1.75. That is, when the S & P 500 return is four percent Bram's expected return would be about seven percent. Thus, the beta is also approximately 1.75 (7 ÷ 4).

6-8B.

+ x Beta =

A 6.75% + (12% - 6.75%) x 1.40 = 14.10%

B 6.75% + (12% - 6.75%) x 0.75 = 10.69%

C 6.75% + (12% - 6.75%) x 0.80 = 10.95%

D 6.75% + (12% - 6.75%) x 1.20 = 13.05%

6-9B. = + (Market Return - Risk-Free Rate) X Beta

= 7.5% + (10.5% - 7.5%) x 0.85

= 10.05%

6-10B. If the expected market return is 12.8 percent and the risk premium is 4.3 percent, the riskless rate of return is 8.5 percent (12.8% - 4.3%). Therefore;

Dupree = 8.5% + (12.8% - 8.5%) x 0.82 = 12.03%

Yofota = 8.5% + (12.8% - 8.5%) x 0.57 = 10.95%

MacGrill = 8.5% + (12.8% - 8.5%) x 0.68 = 11.42%

6-11B.

O'Toole Baltimore

Time Price Return Price Return

1 $22 $45

2 24 9.09% 50 11.11%

3 20 -16.67% 48 -4.00%

4 25 25.00% 52 8.33%

A holding-period return indicates the rate of return you would earn if you bought a security at the beginning of a time period and sold it at the end of the period, such as the end of the month or year,

6-12B.

(a) Sugita Market

Month k_t (k_t - )² k_t (k_t - )²

1 1.80% 0.01% 1.50% 0.06%

2 -0.50 5.68 1.00 0.06

3 2.00 0.01 0.00 1.56

4 -2.00 15.08 -2.00 10.56

5 5.00 9.71 4.00 7.56

6 5.00 9.71 3.00 3.06

Sum 11.30 40.20 7.50 22.86

1.88% 1.25%

(Sum ÷ 6)

22.60% 15.00%

Variance 8.04% 4.58%

(Sum ÷ 5)

2.84% 2.14%

b.

= + (Market Return - Risk-Free Rate) X Beta

= 8% + [(15% - 8%) X 1.18] = 16.26%

c. Sugita's historical return of 22.6 percent exceeds what we would consider a fair return of 16.26 percent, given the stock's systematic risk.

6-13B

a. The portfolio expected return, p, equals a weighted average of the individual stock's expected returns.

p = (0.10)(12%) + (0.25)(11%) + (0.15)(15%) + (0.30)(9%) + (0.20)(14%)

= 11.7%

b. The portfolio beta, ßp, equals a weighted average of the individual stock betas

ßp = (0.10)(1.00) + (0.25)(0.75) + (0.15)(1.30) + (0.30)(0.60) + (0.20)(1.20)

= 0.90

c. Plot the security market line and the individual stocks

d. A "winner" may be defined as a stock that falls above the security market line, which means these stocks are expected to earn a return exceeding what should be expected given their beta or systematic risk. In the above graph, these stocks include 1, 2, 3, and 5. "Losers" would be those stocks falling below the security market line, that being stock 4.

e. Our results are less than certain because we have problems estimating the security market line with certainty. For instance, we have difficulty in specifying the market portfolio.

6-14B

a) Market Hilary’s

Month Price kt (kt- )² Price kt (kt- )²

Jul-02	1328.72			21.00
Aug-02	1320.41	-0.63%	0.0002	19.50	-7.14%	0.0211
Sep-02	1282.71	-2.86%	0.0013	17.19	-11.85%	0.0369
Oct-02	1362.93	6.25%	0.0031	16.88	-1.80%	0.0084
Nov-02	1388.91	1.91%	0.0001	18.06	6.99%	0.0000
Dec-02	1469.25	5.78%	0.0026	24.88	37.76%	0.0924
Jan-03	1394.46	-5.09%	0.0034	22.75	-8.56%	0.0254
Feb-03	1366.42	-2.01%	0.0007	26.25	15.38%	0.0064
Mar-03	1498.58	9.67%	0.0080	33.56	27.85%	0.0419
Apr-03	1452.43	-3.08%	0.0014	43.31	29.05%	0.0470
May-03	1420.60	-2.19%	0.0008	43.50	0.44%	0.0048
Jun-03	1454.60	2.39%	0.0003	43.50	0.00%	0.0054
Jul-03	1430.83	-1.63%	0.0005	43.63	0.30%	0.0050

Sum 8.52% 0.0225 88.42% 0.2948

b) 0.71% 7.37%

Standard deviation 4.52% 16.37%

c)

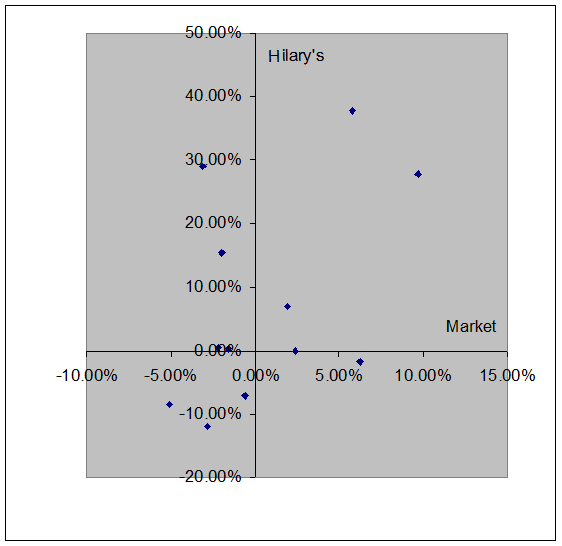d. The Hilary’s returns for the last six months of 2002 and the first six months of 2003 were partially correlated, but with a lot of the variance in the stock’s returns, clearly not explained by the market—as would be expected.

6-15B

Stock A

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

0.10 -4% -0.40% 16.384%

0.30 2 0.60 13.872

0.40 13 5.20 7.056

0.20 17 3.40 13.448

= 8.80% s² = 50.76%

s = 7.125%

Stock B

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

0.13 4% 0.52% 13.658%

0.40 10 4.00 7.225

0.27 19 5.13 6.092

0.20 23 4.60 15.31

= 14.25% s² = 42.285%

s = 6.503%

Stock C

(A) (B) (A) x (B) Weighted

Probability Return Expected Return Deviation

P(ki) (ki) (ki- )²P(ki)

0.20 -2% -0.40% 27.145%

0.25 5 1.25 5.406

0.45 14 6.30 8.515

0.10 25 2.50 23.562

= 9.65% s² = 64.628%

s = 8.039%

Stock B has a higher expected rate of return with less risk than Stocks A and C.

6-16B

+ x Beta =

K 5.5% + (11% - 5.5%) x 1.12 = 11.66%

G 5.5% + (11% - 5.5%) x 1.30 = 12.65%

B 5.5% + (11% - 5.5%) x 0.75 = 9.63%

U 5.5% + (11% - 5.5%) x 1.02 = 11.11%

6-17B

Watkins Fisher

Time Price Return Price Return

1 $40 $27

2 45 12.50% 31 14.81%

3 43 -4.44 35 12.90

4 49 13.95 36 2.86

6-18B

(a) = + Beta

= 4% + 0.95 (7% - 4%)

= 6.85%

(b) = + Beta

= 4 % + 1.25 (7% - 4%)

= 7.75%

(c) If beta is 0.95:

Required rate = 4 % + 0.95 (10% - 4%)

of return

= 9.7%

If beta is 1.25:

Required rate = 4 % + 1.25 (10% - 4%)

of return

= 11.5%

Дата добавления: 2015-10-30