|
Читайте также: |
Определение первообразной
Определение. Первообразной для функции 
называется функция 
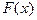такая, что 
Определение неопределенного интеграла
Определение. Совокупность всех первообразных называется неопределенным интегралом и обозначается 
Теорема. Неопределенный интеграл равен
= 
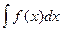где 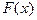любая фиксированная первообразная, а 
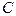- совокупность всех чисел (констант).
Независимость вида неопределенного
Интеграла от выбора аргумента
Теорема. Если 
а 
то
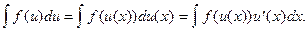
Интегрирование разложением
Определение. Интегрирование разложением называется приведение интеграла с помощью формулы
к сумме (разности) более простых интегралов.
Запомните следующие формулы:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
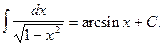
Пример 65.1. 
=34 и 33== 
=36= 
= 
Пример 65.2. 
=43 и Ш= 
- 
30= = 
=36 и 41= 
Метод подстановки в неопределенных интегралах
Определение. Введение новых переменных при вычислении интегралов называется методом подстановки.
Запомните следующие формулы:
Пример 56.1.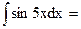 
=Обозначим: 
=
= 
40= 
Второй способ решения этой же задачи: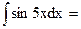
=31 и33= 
40= 
Пример 56.2.
=43 и Ш= - 30= =
=36 и 41=
Пример 56.3. 
31или 51 = = 
= 
= = 
37= 
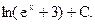
Пример 56.4. 
31или 51 = = 
= = 
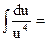36= 
Пример 56.5. Вычислить интеграл 
Под корнем выделим полный квадрат:
30=
= 
47= 
= 
Пример56.7. Вычислить интеграл 
Решение. 
=29,8= 
= = 
38= 
Пример 56.8. Вычислим интеграл 
=Ш= 
= = 
=34;36; 30; 41; Ш=
= 
36; 30; 41= 
+
+ 
= 
Метод интегрирования по частям
Теорема. Если функции 
дифференцируемы, то 
Пример. 
=
Обозначим 
=49= 
= 
=40=
= 
Интегрирование рациональных дробей
Определение. Отношение 
называется рациональной дробью, если 
и 
- многочлены. Если степень числителя меньше степени знаменателя, то рациональная дробь называется правильной. В противном случае она называется неправильной.
Теорема. Для правильной дроби справедлива формула:
+... 
+
+... 
.
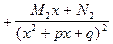Пример. Вычислить 
. Рассмотрим
Ш= 
52=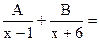 
=Ш== 
Знаменатели равны, значит можно приравнять числители:
Приравниваем коэффициенты при 
и свободные коэффициенты:
Эта система имеет решение: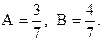 
Поэтому = = 
=30; 37= 
Интегрирование простейших иррациональностей
1. Интеграл 
dx находится с помощью замены: 
Замечание. В этом параграфе 
- рациональная дробь.
2. Интеграл 
находится подстановкой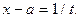 
3. Интеграл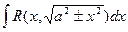 
находится подстановкой 
(соответственно 
).
Примеры. 
(замена 
). 
(замена 
). 
(замена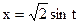 
).
Дата добавления: 2015-10-30; просмотров: 413 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Замена переменных в тройном интеграле | | | ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. |