Замена переменных в тройном интеграле

Пусть функции

(5)

имеют непрерывные частные производные и взаимно однозначно отображают область пространства на область пространства . Если определитель Якóби отображения (5)

не обращается в нуль нигде в области , то переменные определяют не только точку 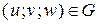, но и соответствующую ей точку 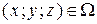в пространстве .

Тем самым числа 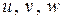можно рассматривать как новые координаты точки , называемые, как и в плоском случае, её криволинейными координатами. Тогда справедлива следующая формула замены переменных в тройном интеграле:

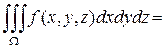
(6)

.

Наиболее часто используемые системы криволинейных координат в пространстве – это цилиндрическая и сферическая системы координат. Они являются пространственными обобщениями плоской полярной системы координат.

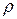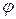При переходе к цилиндрической системе координат прямоугольные координаты заменяют на полярные. Положение точки в пространстве определяется тогда длиной проекции её радиус-вектора на плоскость , углом между этой проекцией и осью 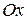, отсчитываемым против часовой стрелки, и координатой (см. рисунок). Формулы перехода имеют вид

, (7)

при этом 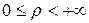, 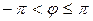(или ), .

Якобиан преобразования (7) , и формула замены переменных (6) принимает вид:

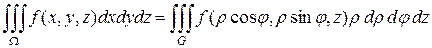. (8)

Цилиндрические координаты удобны при описании круглых цилиндрических областей. Заметим, что при переходе к трёхкратному интегралу за внешнюю переменную, как и в плоском случае, практически всегда берётся угол .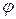

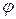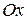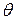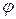В сферической системе координат пространственное положение точки определяется длиной её радиус-вектора, углом между проекцией радиус-вектора на плоскость и осью , и углом между радиус-вектором и осью (см. рисунок). Углы и 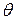отсчитываются от осе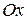й и соответственно. Формулы перехода имеют вид

, (9)

при этом , 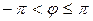(или ), .

Якобиан преобразования (9) . Формула перехода к сферическим координатам в тройном интеграле имеет вид

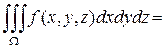
(10)

.

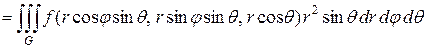Формулы (9) – (10) обычно применяются, когда область интегрирования представляет собой шар или некоторую его часть. При переходе к трёхкратному интегралу за внешнюю переменную, как правило, берётся один из углов 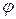или .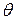

Пример 2.

Перейдём в интеграле примера 1 к сферическим координатам.

Уравнение сферы, ограничивающей шар , в сферических координатах имеет очень простой вид 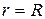. Шар описывается системой неравенств . По формуле (10)

.

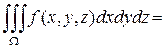
Обратим внимание, что в полученном трёхкратном интеграле все пределы интегрирования постоянные – сравните с примером 1.

Дата добавления: 2015-10-30