
Читайте также:
|
Мета: вивчення принципів функціонування та методики синтезу нейронних мереж (НМ).
ÄКороткі теоретичні відомості
Нейрон – перетворюючий елемент, який має деяку кількість входів (синапсів), на які поступають вхідні сигнали  і один вихід (аксон), з якого знімається вихідний сигнал
і один вихід (аксон), з якого знімається вихідний сигнал  . Кожен синапс має вагу
. Кожен синапс має вагу  , на яку множиться вхідний сигнал
, на яку множиться вхідний сигнал  . Нейронна мережа є сукупністю нейронів, зв'язаних між собою відповідним чином.
. Нейронна мережа є сукупністю нейронів, зв'язаних між собою відповідним чином.
Структура нейрона представлена на рис. 5.1.
Усередині нейрона виділяють блок додавання, що визначає зважену суму всіх вхідних сигналів
 (5.1)
(5.1)
і блок функції активації 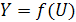 .
.
Таким чином, нейрон функціонує за два такти:
1) підсумовування вхідних сигналів;
2) обчислення Y по функції активації.
Функція активації повинна задовольняти двом умовам:
1) | F(U)| < 1 при будь-якому U
2) функція повинна бути такою, що не монотонною убуває.

Рисунок 5.1 Структура нейрона
Найчастіше в якості функцій активації використовуються наступні функції:
1) ступінчаста функція
 (5.2)
(5.2)
2) сигмоідна функція (рис. 5.2,а)
 (5.3)
(5.3)

а) б)
Рисунок 5.2 – Функції активації
3) гіперболічний тангенс (рис. 5.2,б)
 (5.4)
(5.4)
4) гладкі стискуючі функції
 (5.5)
(5.5)
де Q – поріг (зсув); а - параметр, що визначає крутизну статичної характеристики нейрона.
Нейрони утворюють нейронні мережі шляхом з'єднання синапсів з аксонами.
Найбільш поширеними і добре вивченими є тришарові НС, що складаються з трьох шарів нейронів: вхідного, прихованого і вихідного (рис. 5.3).

Рисунок 5.3 – Нейронна мережа 3-4-2
Нейрони вхідного шару мають тільки по одному синапсу. Кількість нейронів вхідного шару відповідає кількості вхідних змінних мережі Х.
Завданням нейронів цього шару є тільки розподіл вхідних сигналів по нейронах прихованого шару, підсумовування і обчислення функції активації в них не відбувається.
Кількість нейронів в прихованому шарі може бути різною і часто підбирається експериментально. Недостатня або надмірна кількість нейронів в прихованому шарі приводить до погіршення точності апроксимації. Крім того, надмірна кількість ускладнює мережу і зменшує швидкодію.
Нейрони вихідного шару формують вихідні сигнали, їх кількість відповідає кількості виходів Y.
Приклад НМ з 3 вхідними, 4 прихованими і 2 вихідними нейронами приведений на рис.5.3. Така НМ скорочено позначається як (3-4-2). Нij – нейрони.
Дані мережі відносяться до мереж прямого розповсюдження, оскільки в них вхідні сигнали послідовно проходять через всі нейрони і після перетворень безпосередньо подаються на виходи.
Вихідний сигнал yij кожного j-го нейрона в i-му шарі визначається як
 (5.6)
(5.6)
де n(i) – число нейронів в i-му шарі.
Найбільш популярний клас багатошарових мереж|сітей| прямого розповсюдження|поширення| утворюють багатошарові персептрони (MLP|), в яких кожен обчислювальний елемент використовує порогову або сигмоідальну| функцію активації. Багатошаровий персептрон| може формувати дуже складні структури прийняття|прийняття| рішень і реалізовувати довільні булеві функції.
Мережі|сіті|, що використовують радіальні базисні функції (RBF-сети|), є|з'являються| окремим випадком двошарової мережі|сіті| прямого розповсюдження|поширення|. Кожен елемент прихованого шару використовує в якості активаційної функції радіальну базисну функцію гаусового типу|типа| |. Радіальна базисна функція (функція ядра) центрується в точці|точці|, яка визначається ваговим вектором, пов'язаним з нейроном. Кожен вихідний елемент обчислює|обчисляє| лінійну комбінацію цих радіальних базисних функцій. З погляду завдання|задачі| апроксимації приховані елементи формують сукупність функцій, які утворюють базисну систему для представлення вхідних прикладів|зразків| в побудованому|спорудити| на ній просторі.
Нейронні мережі відносяться до класу апроксиматорів і «чорних ящиків», що апроксимують деякі функції вигляду
 (5.7)
(5.7)
де Y – вектор вихідних змінних; Х – вектор вхідних.
Процес апроксимації полягає в підборі вагових коефіцієнтів wij і називається навчанням НМ. Тобто НМ може функціонувати в двох режимах:
- експлуатації, коли на вхід подаються сигнали, а на виході знімаються результати обчислень;
- навчання, коли відбувається коректування вагів так, щоб вихідні сигнали найточніше відповідали бажаним.
Від якості навчання НМ залежить точність її роботи в режимі експлуатації.
Структура процесу навчання представлена на рис. 5.4, де позначені: Yбаж – бажані значення вихідних сигналів, Е – помилка навчання (Е = Yбаж – Y), К – дії, що коректують (зазвичай зміни вагів  ).
).

Рисунок 5.4 – Процес навчання НМ
Для навчання НМ складається навчальна вибірка вхідних сигналів і відповідних їм вихідних. Вибірка може бути розділена на дві частини: робочу вибірку (на основі якої проводиться навчання) і тестову вибірку (для перевірки якості навчання).
Далі визначається структура НМ. Для тришарової НМ кількості вхідних і вихідних нейронів визначаються по кількостям вхідних і вихідних змінних. Кількість нейронів в прихованому шарі Nс може бути взяте з умови:
 (5.8)
(5.8)
де Nin і Nout – кількості нейронів у вхідному і вихідному шарах; Np – кількість навчальних кортежів (об'єм вибірки).
Вагам синапсів ненавченої НМ спочатку привласнюються довільні значення. Далі на вхід НМ подається перший вектор Х з робочої вибірки, визначається вектор Y і помилка навчання Е. Виходячи із значень вектора Е коректуються ваги синапсів. Потім подається наступний вектор Х з вибірки і т.д. Цикли навчання повторюються багато разів, поки якість навчання не стане задовільною, що перевіряється відповідно тестовій вибірці. Існує декілька методів навчання, які класифікують по способах використання вчителя:
- навчання з вчителем (корекція вагів проводиться виходячи з порівняння поточного і бажаного вихідних векторів);
- навчання з послідовним підкріпленням знань (мережі не даються бажані значення виходів, а ставиться оцінка «добре» або «погано»);
- навчання без вчителя (мережа сама виробляє правила навчання шляхом виділення особливостей з набору вхідних даних).
Виходячи з використання елементів випадковості методи навчання підрозділяються:
- на детерміністських (корекція на основі аналізу вхідних і вихідних сигналів, а також додатковій інформації, наприклад, бажаних виходів);
- на стохастичні (випадкова зміна вагів в ході навчання – Больцмановське навчання).
До детерміністських правил навчання|вчення| відносяться правило Хебба, дельта-правило, правило Кохонена, ART-правило|, правило зворотного розповсюдження|поширення|. Найбільш поширеним правилом для мереж|сітей| MLP| є|з'являється| правило зворотного розповсюдження|поширення| (back| propagation|).
Для навчання|вчення| RBF-мереж розроблені різні алгоритми. Основний алгоритм використовує двокрокову| стратегію навчання|вчення|, або змішане навчання|вчення|. Він оцінює позицію і ширину ядра з використанням алгоритму кластеризації "без вчителя|учителя|", а потім алгоритм мінімізації середньоквадратичної помилки "з|із| вчителем|учителем|" для визначення вагів зв'язків між прихованим і вихідним шарами. Оскільки вихідні елементи лінійні, застосовується неітераційний алгоритм. Після|потім| отримання|здобуття| цього початкового наближення використовується градієнтний спуск для уточнення параметрів мережі|сіті|. Цей змішаний алгоритм навчання|вчення| RBF-мережі сходиться набагато швидше, ніж алгоритм зворотного розповсюдження|поширення| для навчання|вчення| багатошарових персептронів|. Проте|однак| RBF-мережа часто містить|утримує| дуже|занадто| велике число прихованих елементів. Це робить повільнішим функціонування RBF-мережі|, ніж багатошарового персептрона. Ефективність (помилка залежно від розміру мережі|сіті|) RBF-мережі і багатошарового персептрона залежать від вирішуваного|рішати| завдання|задачі|.
Правило зворотного розповсюдження
Для навчання|вчення| зазвичай|звично| використовується НМ з|із| функціями активації сигмоідного| типу|типа|. Метою|ціллю| навчання|вчення| за правилом зворотного розповсюдження|поширення| є|з'являється| мінімізація помилки навчання|вчення|, яка визначається як
 (5.9)
(5.9)
Для зменшення помилки ваги змінюються за правилом
 (5.10)
(5.10)
де n - константа, що характеризує швидкість навчання.
Дана формула описує процес градієнтного спуску в просторі вагів.
Алгоритм зворотного розповсюдженням складається з наступних кроків.
1°. На вхід НМ подається вектор Х з навчальної вибірки і обчислюються виходи всіх нейронів Yij.
2°. Визначається величина градієнта помилки EI для кожного нейрона вихідного шару:
 (5.11)
(5.11)
де Yj – вихід j-го нейрона вихідного шару.
3°. Рухаючись від останнього шару до першого визначаються градієнти EIij длякожного j-го нейрона кожного i-го шару:
 (5.12)
(5.12)
де k – номер синапсу, що сполучає нейрон Нij з нейроном Нi+1,k наступного шару.
4°. Корекція вагів синапсів:
 (5.13)
(5.13)
Корекція вагів для вхідного шару не проводиться.
5°. Якщо повчальна вибірка не закінчилася, то кроки 1 – 5 повторюються.
6°. Визначається величина помилки Е. Якщо вона не задовільна, то кроки 1 – 6 повторюються.
З описаного алгоритму видно, що процес навчання НМ включає два вкладені цикли навчання: внутрішній цикл (кроки 1 – 5) повторюється відповідно кількості прикладів з повчальної вибірки, зовнішній (кроки 1 – 6) – до тих пір, поки не буде досягнута задовільна (з погляду помилки Е) якість навчання.
Після успішного навчання НМ може бути протестована на тестовій вибірці. Якщо помилка навчання на кожному прикладі з тестової вибірки задовільна, то НМ можна вважати навченою і приступати до її експлуатації.
Приклад одного циклу навчання НС.
Вхідні навчальні кортежі наведені нижче:
| х1 | х2 | у |
де х1 і х2 – вхідні параметри НМ, у – бажаний вихідний параметр.
Оскільки у функції, що апроксимується, два вхідні параметри і один вихідний, то вибирається НМ з двома нейронами у вхідному шарі і одним у вихідному. Кількість нейронів прихованого шару приймемо рівним двом, тобто формується мережа виду 2-2-1 (рис. 5.5).

Рисунок 5.5 – Приклад НМ 2-2-1
Як функція активації вибирається сигмоідна функція з коефіцієнтом  . Початкові значення ваг синаптичних зв'язків приймаємо рівними 0,5:
. Початкові значення ваг синаптичних зв'язків приймаємо рівними 0,5:

Оскільки початкові значення х1, х2 і у не лежать в межах [0, 1], їх необхідно пронормувати, поділивши, наприклад, х1 на 4, х2 на 2, а у на 16. В результаті отримуємо нормовану вибірку:
| х1 | х2 | у |
| 0,25 | 0,125 | |
| 0,5 | 0,5 | 0,375 |
Швидкість навчання приймається рівною n = 0,2.
Розглянемо кроки навчання.
1°. На входи НМ подається перший вектор вхідних параметрів:
х1 = 0,25 і х2 = 0 (убаж = 0,125).
Виходи нейронів вхідного шару: Y11 = 0,25, Y12 = 0.
Для прихованого шару:
U21 =  ×Y11 +
×Y11 +  ×Y12 = 0,5×0,25 + 0,5×0 = 0,125;
×Y12 = 0,5×0,25 + 0,5×0 = 0,125;
U22 =  ×Y11 +
×Y11 + 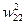 ×Y12 = 0,5×0,25 + 0,5×0 = 0,125;
×Y12 = 0,5×0,25 + 0,5×0 = 0,125;
Y21 = 1 / (1 + exp(-a×U21)) = 1 / (1 + exp(-0,125)) = 0,5312;
Y22 = 1 / (1 + exp(-a×U22)) = 1 / (1 + exp(-0,125)) = 0,5312.
Для вихідного шару:
U31 =  ×Y21 +
×Y21 +  ×Y22 = 0,5×0,5312 + 0,5×0,5312 = 0,5312;
×Y22 = 0,5×0,5312 + 0,5×0,5312 = 0,5312;
Y31 = 1 / (1 + exp(-a*U31)) = 1 / (1 + exp(-0,5312)) = 0,6298.
2°. Величина градієнта для вихідного нейрона
EI31 = (Y31 – Yбаж) ×Y31× (1 – Y31) = (0,6298 – 0,125) ×0,6298× (1 - 0,6298) = 0,1177.
3°. Величини градієнтів для прихованого шару:
EI21 = Y21× (1 – Y21) × [EI31×  ] = 0,5312× (1 – 0,5312) ×0,1177×0,5 = 0,01466
] = 0,5312× (1 – 0,5312) ×0,1177×0,5 = 0,01466
EI22 = Y22× (1 – Y22) × [EI31×  ] = 0,5312× (1 – 0,5312) ×0,1177×0,5 = 0,01466.
] = 0,5312× (1 – 0,5312) ×0,1177×0,5 = 0,01466.
4°. Корекція вагів синапсів:
 =
=  - n× Y11× EI21 = 0,5 – 0,2× 0,25× 0,01466 = 0,4993
- n× Y11× EI21 = 0,5 – 0,2× 0,25× 0,01466 = 0,4993
 =
=  - n× Y11× EI22 = 0,5 – 0,2× 0,25× 0,01466 = 0,4993
- n× Y11× EI22 = 0,5 – 0,2× 0,25× 0,01466 = 0,4993
 =
=  - n× Y12× EI21 = 0,5 – 0,2× 0× 0,01466 = 0,5
- n× Y12× EI21 = 0,5 – 0,2× 0× 0,01466 = 0,5
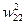 =
= 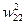 - n× Y12× EI22 = 0,5 – 0,2× 0× 0,01466 = 0,5
- n× Y12× EI22 = 0,5 – 0,2× 0× 0,01466 = 0,5
 =
=  - n× Y21× EI31 = 0,5 – 0,2× 0,5312× 0,1177 = 0,4875
- n× Y21× EI31 = 0,5 – 0,2× 0,5312× 0,1177 = 0,4875
 =
=  - n× Y22× EI31 = 0,5 – 0,2× 0,5312× 0,1177 = 0,4875.
- n× Y22× EI31 = 0,5 – 0,2× 0,5312× 0,1177 = 0,4875.
Якщо при отриманих вагах на вхід НМ подати той же вектор вхідних параметрів, то на виході буде у = 0,6267, що вже ближче до бажаного убаж = 0,125. Тобто даний цикл навчання наблизив відповідь НМ до бажаного на величину  у = 0,6298 – 0,6267 = 0,0031.
у = 0,6298 – 0,6267 = 0,0031.
Оскільки повчальна вибірка не закінчилася, то кроки 1 – 4 повторюються аналогічно для наступного вектора вхідних параметрів.
Варіанти завдань
Необхідно:
1) Отримати завдання згідно варіанту табл. 5.1.
Таблиця 5.1 – Варіанти завдань
| Варіант | Завдання |
у = 2 × sin2x, х  [0, 1] [0, 1]
| |

| |
| y1 = 0.5 × x2 – 4.8 × x + 3.5, y2 = x3 – 12, y3 = x + 3,5 | |
  x1, x2 x1, x2  [1, 10] [1, 10]
| |
y1 = |x1 – x2|, y2 = x1 + x2, y3 = x1 × x2; x1, x2  [1, 10] [1, 10]
| |
y1 = x1 × sin(x2), y2 = x1 × cos(x2); x1  [1, 10], x2 [1, 10], x2  [-90°, +90°] [-90°, +90°]
| |
y1 = x1 × x2 + x3, y2 = 2 × y1; x1, x2, x3  [1, 10] [1, 10]
| |
y1 = 1,5 × x1 + |x2 – 2 × x3|, y2 = x3 – y1; x1, x2, x3  [1, 10] [1, 10]
| |
 , ,  ; x1, x2 ; x1, x2  [-10, 10] [-10, 10]
| |
y1 = 2,3 × x1 × x2 – 0,5 × 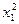 + 1,8 × x2, y2 = + 1,8 × x2, y2 =  ; x1, x2 ; x1, x2  [1, 10] [1, 10]
| |
| Y1 = X1 AND X2, Y2 = X1 OR X2, Y3 = NOT X1 | |
| Y = X1*X2 + X3*X4 | |

| |

| |

| |
у = 2 × x1 + 5 × x1 × x2 + x2; x1, x2  [-5, 5] [-5, 5]
| |
у = sin x1 × sin x2 × sin x3; x1, x2, x3  [0, p] [0, p]
| |
у = 2 × x1 × cos x2, x1  [0,1], x2 [0,1], x2  [0, p] [0, p]
| |
у = x1 + x2 + x3, xi  [0, 10] [0, 10]
|
У варіантах 1 – 10 і 16 – 19 необхідно за допомогою нейронної мережі провести апроксимацію функції виду Y = f(X) на заданому інтервалі Х, де Х – вектор вхідних змінних Х = { х1, х2…}, Y – вектор вихідних змінних. Діапазони зміни вхідних змінних вказані в таблиці.
Варіанти 11 – 15: апроксимація логічних функцій декількох змінних Хi, вихідна змінна Y – логічна. Розглядається вся область визначення функції.
2) Підготувати повчальну вибірку засобами|коштами| додатку|застосування| Microsoft| Excel| і оформити її у вигляді файлу *.csv (для завдань|задач| апроксимації алгебраїчних функцій).
Примітка: Щоб створити набір випадкових чисел, скористайтеся функцією: =СЛЧИС()*100. У сусідньому стовпці розрахуйте значення заданої функції. Збережіть файл, вибравши розширення.CSV.
3) Провести навчання декількох нейронних мереж за допомогою програмного нейроімітатору.
Розглядаються п'ять варіантів мережі: MLP з кількістю нейронів в прихованому шарі, рівному 1, 3, 5, 7 і функцією активації «сигмоідна» (Logistic). Навчання кожної мережі вести, наприклад, в 100 кроків. Навчання вести по алгоритму зворотного розповсюдження.
4) Перевірити якість кожної навченої мережі, для чого розрахувати декілька значень вихідний змінної по заданій функції і по нейронній мережі, потім на графіці показати близькість кожної навченої моделі до початкової.
5) Розрахувати уручну одне вихідне значення нейронної мережі (для MLP мережі з п’ятьма нейронами в прихованому шарі). Порівняти із значенням, розрахованим за допомогою нейроімітатора.
ÄКороткі теоретичні відомості
Дата добавления: 2015-10-29; просмотров: 255 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Визначення граничних абсолютних і відносних | | | Крок 4. Задайте параметр навчання |