Тақырыбы: Қателікті анықтайтын ақаулықты қорғауды коды

Жұмыстың мақсаты: Ақаулықтықорғауды кодын құру методымен үйрету.

Тапсырма: Хэммин кодын құру.

Мысал 1. Хэмминг әдісі арқылы кодтау мен кодтамау ретін қараймыз.

Кодтау:

Контрольдік символдың санын анықтау.

Кесте 1.Контрольды символдар саны m, Хэмминг кодында информациялық символдар k тәуелді.

k

m

Контрольдық символдарды орналастыру.1,2,4,8 позициясында яғни, екі дәрежелі орындарда шыққан символдарды табу үшін ыңғайлап орналастыру.Қалған орындарда ақпараттық символдар орналасады,сондақтан Мысал.7 элементті кодталған комбинация үшін жазуға болды:

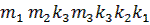
Осыдан 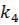2-лік кодталған комбинациядағы үшінші немесе төртінші разряд, кікентай немесе бірінші разряд.

Екілік санақ қатары	Кодтың символы	Екілік санақ қатары	Кодтың символы
3(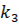)	2(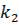)	1()	3(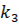)	2(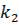)	1()

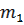
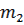
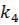
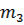
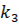
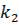
Символдардың құрамындағы бақылаушыларын анықтау.

Кесте 2.Хэмминг кодына арналған тексеруші кесте құрастыру.

Кесте 2-де барлық кодтық комбинация (Нөлдік кірмегенде) төртразрядтық екілік кодта барлық,оң жағынан төменнен жоғары қарай Хэмминг кодыдының комбинация символдар орналасқан.

2-ші кестеде 3 қатарда жазылған келесі заңдылықтар 3-ші кесте құрастырылады.

Кесте 3-Хэмминг кодына тексерістік кестесі.

Коддтау кезінде ұзағырақ комбинация 2-ші және 3-ші кестеде толық көрсетілген.

Қорытынды сұрақтар:

1.Қандай кодтар ақаутұрақтылық деп аталынады?

2.Корректорлық қабілет кодымен, кодтық ара-қашықтық қалай байланысады?

3. Ақаутұрақтылық ұзындық кодын қалай анықтайды?

4.Кодтың артықшылығын қалай анықтайды?

5.Дұрыс комбинацияны тексеру қандай методпен анықталады?

Ұсынылған әдебеттер:

2,3 негізгі

2, 5, 6 қосымша

БӨЖ №14. Сызықты топтық кодалар. Құрылатын матрицаға мысалдар (6 сағат).

1. Топты екілік кодты құру.Табушы кодтар.

2. Табушы кодтарға мысалдар

Есеп шығару.

Тақырыбы: Құру тәсілінің ақаусыз қорғалған кодтары

Жұмыстың мақсаты: Құру тәсілінің ақаусызқорғалған кодтарын үйрену

Тапсырма.

1. Екілік-ондық кодты құру.

Шешімі. Ондық санның әр разряды екілік кодтың комбинациясы түрінде жазылады. Мысалы, ондық жүйедегі 9 саны екілік жүйеде 1001 болып, ал 3 саны 0011 болып жазылады. Сондықтан 399 саны екілік-ондық жүйеде 001110011001 түрде болады.

2. Грей кодын құру.

Мысал 1.

Оның құрылымы екілік кодтың жазу формасының барлық үйлесіміне сәйкес келеді.

Қарапайым екілік кодтың маскасын қолданғанда қателік минимальды болуы мүмкін, егер Ол кіші разрядта туындаса және сәйкесінше үлкен разрядта максимальды болады. Жалпы жағдайда, егер үлкен разряд n нөмерлі болса, онда максимальды қателік 2^n-1-ге тең. Осындай қателіктерді болдырмау мақсатында қарапайым екілік кодтың орнына бір саннан екіншіге көшкенде комбинациясы тек бір разрядта өзгеретін, және,сәйкесінше, кодтық маскасы кез келген разрядтағы өзгерістер кезінде қателік 1-ге тең болатындай етіп құрылатын кодтар қолданылады. Осындай кодтарға Грей коды да жатады.

Қарапайым екілік код Грей кодына берілген комбинацияның 2-ші модульі бойынша суммалау жолымен түрлендіріледі, бірақ оңға бір разряд жылжытлған. Мысалы, екілік сандар 1101 мен 1010 Грей кодына түрлендірілуі келесі түрде болады:

ө 1101

Қосу барысында екінші қосылғыштың кіші разряды серпіледі.

Грей кодын екілік жүйеге түрлендіру Грей коды сандарының суммасын қосу арқылы кіші разрядтан басталып, үлкен разрядтан бастап және түрленетін разрядтан аяқталатындайетіп орындалады. Егер 2-ші модуль бойынша қосу барысында сумма жұп болса, 0 жазылады, тақ болса, 1 жазылады. Мысалы, Грей коды комбинациясын аудару барысында 1011 екілік код комбинациясының кіші разрядында 1 жазылады, өйткені 1Ө1Ө1=1. Екінші разраядта 0 болады, өйткені 1Ө1=0. Үшінші разраядта 1 жазылады, өйткені 3 разрядта Грей коды 0-ді құрайды, ал төртіншіде 1-ді. Соңғы разрядта да 1 жазылады, өйткені соңғы разрядта да Грей коды 1-ді құрайды. Осылайша, рефлексті кодтың комбинациясы 1011 екілік кодта 1101 түрін қабылдайды.

Дата добавления: 2015-10-23