
Читайте также:
|
Движение точки M - сложное. Её абсолютное движение складывается из движения по стороне ВД пластины – относительное движение и движения точки М вместе с вращающейся пластиной – переносное движение.
Абсолютная скорость точки М
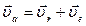 ,
,
где 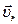 – относительная скорость
– относительная скорость  ;
;
 – переносная скорость
– переносная скорость  ;
;
Абсолютное ускорение точки
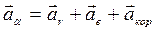
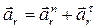
 ,
,
где  – относительное ускорение;
– относительное ускорение;
 – переносное ускорение,
– переносное ускорение,
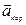 – ускорение Кориолиса,
– ускорение Кориолиса,
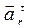 – - относительное касательное ускорение,
– - относительное касательное ускорение,
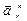 – относительное нормальное ускорение.
– относительное нормальное ускорение.
 – переносное касательное ускорение,
– переносное касательное ускорение,
 – переносное нормальное ускорение.
– переносное нормальное ускорение.
Рассмотрим относительное движение точки.
Скорость относительного движения
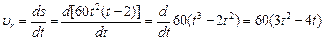

Относительное касательное ускорение


Относительное нормальное ускорение

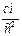 , так как точка M в относительном движении перемещается по прямой BD, то
, так как точка M в относительном движении перемещается по прямой BD, то  , тогда
, тогда 
Модуль относительного ускорения 
Для момента времени t=1 c:
AM= 
 (знак минус показывает, что движение направлено от точки А к точке В);
(знак минус показывает, что движение направлено от точки А к точке В);
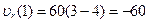

(вектор 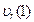 направлен к B);
направлен к B);
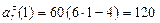
 (вектор направлен к точке D);
(вектор направлен к точке D);
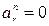
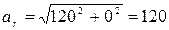 (
( )
)
Строим чертеж с нанесением положения точки, векторов относительных скорости и ускорения в момент t = 1 c

Рис.1.2
Переносное движение
Угловая скорость переносного движения  , следовательно, угловое переносное ускорение
, следовательно, угловое переносное ускорение
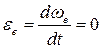
Переносная скорость точки M

В момент времени t=1c
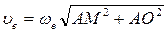
Переносное касательное ускорение

Переносное нормальное ускорение
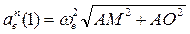
Кориолисово ускорение

(вектор 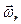 направлен вдоль оси вращения)
направлен вдоль оси вращения)
Вектор  перпендикулярен плоскости, в которой расположены векторы
перпендикулярен плоскости, в которой расположены векторы  и
и  и направлен в ту сторону, чтобы с его конца поворот вектора
и направлен в ту сторону, чтобы с его конца поворот вектора 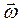 (первый сомножитель) до совмещения его с вектором
(первый сомножитель) до совмещения его с вектором  (второй сомножитель) по кратчайшему пути был виден происходящим против хода стрелки часов.
(второй сомножитель) по кратчайшему пути был виден происходящим против хода стрелки часов.
Абсолютное движение
Абсолютная скорость точки М

Сумму векторов найдем через проекции на оси координат X и У

 (
( )
)










Рис.1.3
Абсолютное ускорение
Абсолютное ускорение точки М для нашего случая

Сумму векторов найдем через их проекции на оси координат X и У

для момента времени t=1c

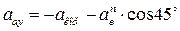

 ( см/с2)
( см/с2)
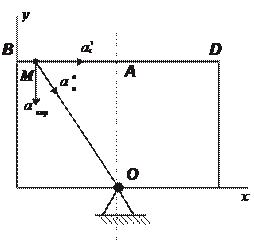
Рис.1.4
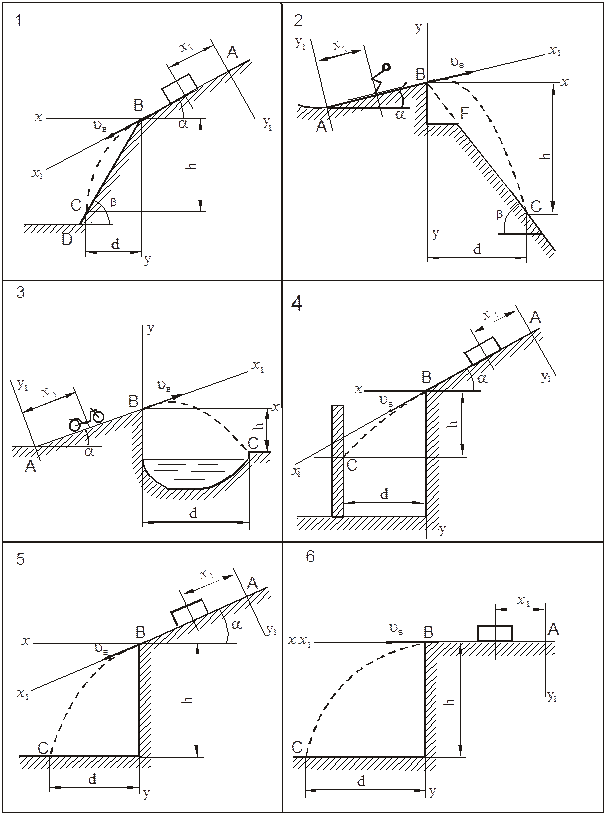
3. Задача 2. «Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил»
Варианты 1 – 5 (схема 1). Тело движется из точки А по участку АВ (длиной  ) по наклонной плоскости, составляющей угол
) по наклонной плоскости, составляющей угол  с горизонтом, в течение
с горизонтом, в течение  с. Его начальная скорость
с. Его начальная скорость  . Коэффициенттрения скольжения тела по плоскости равен
. Коэффициенттрения скольжения тела по плоскости равен  .
.
В точке В тело покидает плоскость со скоростью 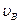 и попадает со скоростью
и попадает со скоростью  в точку С плоскости BD, наклоненной под углом
в точку С плоскости BD, наклоненной под углом  к горизонту, находясь в воздухе Т с.
к горизонту, находясь в воздухе Т с.
При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать.
Вариант 1. Дано:  = 30°;
= 30°;  = 0,
= 0,  = 0,2
= 0,2  = 10м,
= 10м,  =60°. Определить
=60°. Определить  и
и 
Вариант 2. Дано:  = 15°;
= 15°;  =2м/с,
=2м/с,  = 0,2,
= 0,2,  = 4м,
= 4м,  =45°. Определить
=45°. Определить  и уравнение траектории точки на участке BC.
и уравнение траектории точки на участке BC.
Вариант 3. Дано:  = 30°;
= 30°;  = 2,5м/с,
= 2,5м/с,  ≠ 0,,
≠ 0,,  = 8м, d = 10м,
= 8м, d = 10м,  =60°. Определить
=60°. Определить  и
и 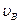
Вариант 4. Дано:  =0,
=0,  = 2с,
= 2с,  = 0;
= 0;  =9,8м;
=9,8м;  =60°. Определить
=60°. Определить  и T.
и T.
Вариант 5. Дано:  = 30°;
= 30°;  =0,
=0,  = 3с,
= 3с,  =9,8м;
=9,8м;  =45°. Определить
=45°. Определить  и
и 
Варианты 6 - 10 (схема 2). Лыжник подходи к точке А участка трамплина
АВ, наклоненного под углом  к горизонту и имеющего длину
к горизонту и имеющего длину  , со скоростью
, со скоростью  .
.
Коэффициент трения скольжения лыж на участке АВ равен  . Лыжник от А до В движется
. Лыжник от А до В движется  с; в точке B со скоростью
с; в точке B со скоростью 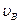 он покидает трамплин. Через Т с лыжник приземляется со скоростью
он покидает трамплин. Через Т с лыжник приземляется со скоростью  в точке С горы, составляющей угол
в точке С горы, составляющей угол  с горизонтом
с горизонтом
При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.
Вариант 6. Дано: 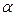 = 20°,
= 20°,  = 0,1,
= 0,1,  = 40м,
= 40м,  =30°.
=30°.
Определить  и
и 
Вариант 7. Дано:  = 15°;
= 15°;  = 16 м/с,
= 16 м/с,  = 0,1
= 0,1  = 5м,
= 5м,  =45°.
=45°.
Определить 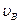 и T.
и T.
Вариант 8. Дано:  = 21м/с,
= 21м/с,  = 0,
= 0,  = 3с,
= 3с, 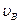 = 20м/с,
= 20м/с,  =60°.
=60°.
Определить  и d
и d
Вариант 9 Дано:  = 15°;
= 15°;  = 3с,
= 3с,  = 0,1,
= 0,1,  =
=  м,
м,  =45°. Определить
=45°. Определить 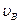 и
и  .
.
Вариант 10. Дано:  = 15°;
= 15°;  = 12м/с,
= 12м/с,  = 0, d = 50м,
= 0, d = 50м,  =60°. Определить
=60°. Определить  и уравнение траектории лыжника на участке BC.
и уравнение траектории лыжника на участке BC.
Варианты 11 – 15 (схема 3). Имея в точке А скорость  , мотоцикл поднимается
, мотоцикл поднимается  с по участку АВ длиной
с по участку АВ длиной  , составляющему с горизонтом угол
, составляющему с горизонтом угол 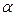 . При постоянной на всем участке АВ движущей силе Р мотоцикл в точке В приобретает скорость
. При постоянной на всем участке АВ движущей силе Р мотоцикл в точке В приобретает скорость 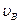 и перелетает через ров шириной d,находясь в воздухе Тс и приземляясь в точке С со скоростью
и перелетает через ров шириной d,находясь в воздухе Тс и приземляясь в точке С со скоростью  . Масса мотоцикла с мотоциклистом равна т.
. Масса мотоцикла с мотоциклистом равна т.
При решении задачи считать мотоцикл с мотоциклистом материальной точкой и не учитывать силы сопротивления движению.
Вариант 11. Дано:  = 30°; Р ≠ 0;
= 30°; Р ≠ 0;  = 40 м;
= 40 м;  = 0:
= 0: 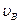 = 4,5 м/с; d = 3 м. Определить
= 4,5 м/с; d = 3 м. Определить  и
и  .
.
Вариант 12. Дано:  = 30°; Р = 0;
= 30°; Р = 0;  = 40 м;
= 40 м; 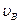 = 4,5 м/с;
= 4,5 м/с;  = 1,5 м. Определить
= 1,5 м. Определить  и d.
и d.
Вариант 13. Дано:  = 30°; т = 400 кг,
= 30°; т = 400 кг,  = 0;
= 0;  = 20 с; d = 3 м;
= 20 с; d = 3 м;  =1,5 м. Определить Р и
=1,5 м. Определить Р и  .
.
Вариант 14. Дано:  = 30°; т = 400 кг; Р = 2,2 кН;
= 30°; т = 400 кг; Р = 2,2 кН;  = 0;
= 0;  = 40 м;: d = 5 м. Определить
= 40 м;: d = 5 м. Определить 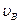 и
и  .
.
Вариант 15. Дано:  = 30°;
= 30°;  = 0; Р = 2 кН,
= 0; Р = 2 кН,  = 50 м;
= 50 м;  =50 м, d = 4 м. Определить Т и т
=50 м, d = 4 м. Определить Т и т
Варианты 16 – 20 (схема 4). Камень скользит в течение  с, по участку АВ откоса, составляющему угол
с, по участку АВ откоса, составляющему угол  с горизонтом и имеющему длину
с горизонтом и имеющему длину  . Его начальная скорость
. Его начальная скорость  . Коэффициент трения скольжения камня по откосу равен
. Коэффициент трения скольжения камня по откосу равен  Имея в точке В скорость
Имея в точке В скорость 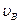 , камень через Т с ударяется; в точке С о вертикальную защитную стену.
, камень через Т с ударяется; в точке С о вертикальную защитную стену.
При решении задачи принять камень за материальную точку; сопротивление воздуха не учитывать.
Вариант 16. Дано:  = 30°;
= 30°;  = 1 м/с;
= 1 м/с;  = 3 м;
= 3 м;  = 0,2; d = 2,5 м. Определить
= 0,2; d = 2,5 м. Определить  и Т.
и Т.
Вариант 17. Дано:  = 45°;
= 45°;  = 6 м;
= 6 м; 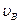 = 2
= 2  ;
; 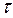 = 1 с;
= 1 с;  = 6 м. Определить d и f.
= 6 м. Определить d и f.
Вариант 18. Дано:  = 30°;
= 30°;  = 2 м;
= 2 м;  = 0 м/с,
= 0 м/с,  = 0,2; d = 3 м,
= 0,2; d = 3 м,
Определить  и
и 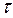 .
.
Вариант 19. Дано:  = 15°;
= 15°;  =3 м;
=3 м; 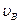 = 3 м/с,
= 3 м/с,  ≠ 0;
≠ 0;  = 1,5 с; d = 2 м,
= 1,5 с; d = 2 м,
Определить  и
и  .
.
Вариант 20. Дано:  = 45°,
= 45°,  = 0;
= 0;  = 0,3; d = 2 м;
= 0,3; d = 2 м;  = 4 м. Определить
= 4 м. Определить  и
и  .
.
Варианты 21 – 25 (схема 5). Тело движется из точки А по, участку АВ (длиной  ) наклонной плоскости, составляющей угол
) наклонной плоскости, составляющей угол  с горизонтом. Его начальная скорость
с горизонтом. Его начальная скорость  . Коэффициент трения скольжения равен
. Коэффициент трения скольжения равен  . Через
. Через  с тело в точке В со скоростью
с тело в точке В со скоростью 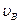 покидает наклонную плоскость и падает на горизонтальную плоскость в точку С со скоростью
покидает наклонную плоскость и падает на горизонтальную плоскость в точку С со скоростью  , при этом оно находится в воздухе Т с.
, при этом оно находится в воздухе Т с.
При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха.
Вариант 21. Дано:  = 30°;
= 30°;  = 1 м/с;
= 1 м/с; 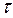 = 1,5 с;
= 1,5 с;  = 0,1;
= 0,1;  = 10 м. Определить
= 10 м. Определить 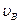 и d.
и d.
Вариант 22. Дано:  = 45°;
= 45°;  = 10 м;
= 10 м;  = 0;
= 0; 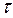 = 2 с;.Определить
= 2 с;.Определить  иуравнение траектории на участке BC.
иуравнение траектории на участке BC.
Вариант 23. Дано:  = 9,81 м;
= 9,81 м;  = 0 м/с,
= 0 м/с,  = 0;
= 0;  = 20 м,
= 20 м, 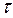 = 2 с, Определить
= 2 с, Определить  и T
и T
Вариант 24. Дано:  = 30°;
= 30°;  =10 м;
=10 м;  = 0 м/с,
= 0 м/с,  = 0,2; d = 12 м,
= 0,2; d = 12 м,
Определить 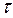 и
и  .
.
Вариант 25. Дано:  = 30°,
= 30°,  = 0;
= 0;  = 0,2;
= 0,2;  = 4,5 м;
= 4,5 м;  = 6 м. Определить
= 6 м. Определить  и
и  .
.
Варианты 26 – 30 (схема 6). Имея в точке А скорость  , тело движется по горизонтальному участку АВ длиной
, тело движется по горизонтальному участку АВ длиной  в течение
в течение  с. Коэффициент скольжения тела по плоскости равен
с. Коэффициент скольжения тела по плоскости равен  . Со скоростью
. Со скоростью 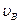 тело в точке B покидает плоскость и попадает в точку С со скоростью
тело в точке B покидает плоскость и попадает в точку С со скоростью  , находясь в воздухе T с. При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.
, находясь в воздухе T с. При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.
Вариант 26. Дано:  = 7 м/с;
= 7 м/с;  = 8 м,
= 8 м,  = 0,2;
= 0,2;  = 20 м.
= 20 м.
Определить  и d.
и d.
Вариант 27. Дано: d = 2 м;  = 4 м/с;
= 4 м/с; 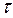 = 2 с;
= 2 с;  = 0,1.
= 0,1.
Определить 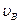 и
и  .
.
Вариант 28. Дано:  = 3 м;
= 3 м; 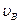 =3 м/с,
=3 м/с,  = 0,3;
= 0,3;  = 5 м.
= 5 м.
Определить  и T
и T
Вариант 29. Дано:  =2,5 м;
=2,5 м;  = 3 м/с,
= 3 м/с, 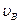 =1 м/с,
=1 м/с,  = 20 м.
= 20 м.
Определить  и d.
и d.
Вариант 30. Дано:  = 0,25;
= 0,25;  = 5 м;
= 5 м;  = 4 м, d = 3 м.
= 4 м, d = 3 м.
Определить  и
и  .
.
Дата добавления: 2015-10-29; просмотров: 155 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример решения Задачи 1 | | | Пример решения Задачи 2 |