
Читайте также:
|
В железнодорожных скальных выемках кюветов от попадания в них с откосов каменных осыпей устанавливается «полка» DC. Учитывая возможность движения камня из наивысшей точки А откоса и полагая при этом его начальную скорость  = 0, определить наименьшую ширину полки b и скорость
= 0, определить наименьшую ширину полки b и скорость  , с которой камень падает на нее. По участку АВ откоса, составляющему угол α с горизонтом и имеющему длину
, с которой камень падает на нее. По участку АВ откоса, составляющему угол α с горизонтом и имеющему длину  , камень движется
, камень движется  с. При решении задачи считать коэффициент трения скольжения
с. При решении задачи считать коэффициент трения скольжения  камня на участке AB постоянным, а сопротивлением воздуха пренебречь.
камня на участке AB постоянным, а сопротивлением воздуха пренебречь.
Дано: 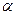 = 60°;
= 60°;  = 0 м/с,
= 0 м/с,  ≠ 0,
≠ 0,  = 4м,
= 4м,  = 1 с,
= 1 с,  =75°. Определить
=75°. Определить  и b.
и b.

Решение: рассмотрим движение камня на участке АВ. Принимая камень за материальную точку, покажем действующие на него силы: вес  , нормальную реакцию
, нормальную реакцию  и силу трения скольжения
и силу трения скольжения  . С оставим дифференциальное уравнение движения камня на участке АВ:
. С оставим дифференциальное уравнение движения камня на участке АВ:


Сила трения
 где
где 
Таким образом

или 
интегрируя дифференциальное уравнение дважды получаем:


Для определения постоянных интегрирования воспользуемся начальными условиями задачи: при t = 0, x 01=0 и 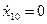 *
*
Составим уравнения, полученные при интегрировании, для t=0:


Найдем постоянные С1 = 0, С2 = 0
тогда

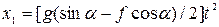
Для момента  , когда камень покидает участок,
, когда камень покидает участок,


т.е


откуда
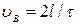
т.е.

Рассмотрим движение камня от точки В до точки С.
Показав силу тяжести  , действующую на камень, составим дифференциальные уравнения его движения:
, действующую на камень, составим дифференциальные уравнения его движения:


Начальные условия задачи; при t = 0
x0=0, y0 = 0
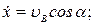
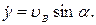
Интегрируем дифференциальные уравнения


x = C 3 t + C 5, y = gt 2/2 + C 4 t + C 5.
Напишем полученные уравнения для t = 0


x = C 5; y = C 6.
Отсюда найдем, что


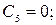

Получим следующие уравнения проекций скоростей камня:
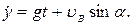
И уравнения его движения:


Уравнение траектории камня найдем, исключив параметр t из уравнений движения. Определив t из первого уравнения и подставив его значение во второе, получаем уравнение параболы:
В момент падения y = h, x = d.
Определяя d из уравнения траектории, найдем
d 1 = 2,11 м, d 2 = –7,75 м.
Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то d = 2,11 м.
Минимальная ширина полки
b = d – ED = d – h/tg75°, или b = 0,77 м.
Используя уравнение движения камня 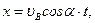 найдем время Т движения камня от точки В до точки С: Т = 0,53 с.
найдем время Т движения камня от точки В до точки С: Т = 0,53 с.
Скорость камня при падении найдем через проекции скорости на оси координат
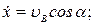
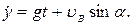
По формуле

Для момента падения t = T = 0,53с

или

4. Задача 3. «Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела»
Тело Н массой m1 вращается вокруг вертикальной оси z с постоянной угловой скоростью wо; при этом в точке О желоба АВ тела Н на расстоянии АО от точки А, отсчитываемом вдоль желоба, находится материальная точка К массой т2. В некоторый момент времени (t = 0) на систему начинает действовать пара сил с моментом Mz = Мz (t). При t = х действие прекращается.
Определить угловую скорость wt тела Н в момент t = t.
Тело Н вращается по инерции с угловой скоростью wt.
В некоторый момент времени t1 = 0 (t1 – новое начало отсчета времени) точка К (самоходный механизм) начинает относительное движение из точки О вдоль желоба AВ (в направлении к В) по закону ОК = s = s (t1).
Определить угловую скорость w T тела Н при t1 = Т.
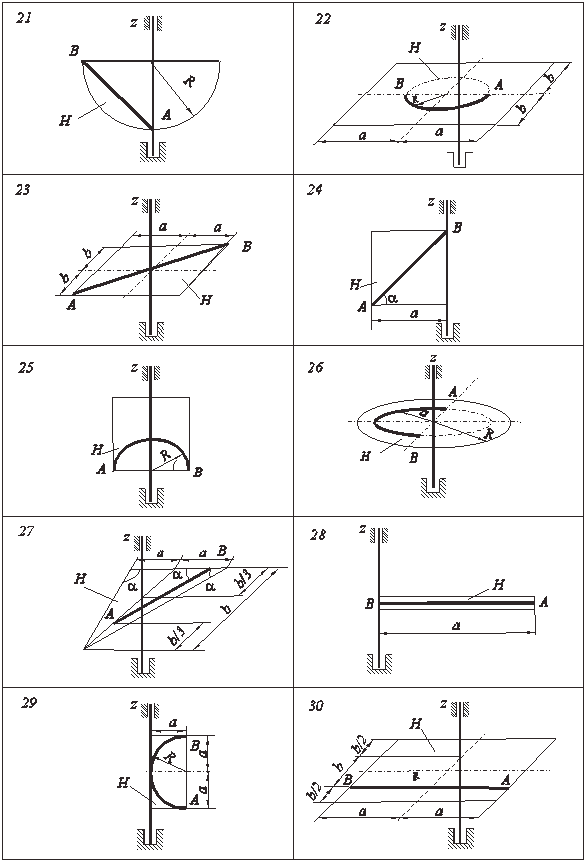
Тело Н рассматривать как однородную пластинку, имеющую форму. Необходимые для решения данные приведены в таблицах.
Рисунки к соответствующим вариантам задач, приведены на страницах 25-27.
| Номер варианта | т1, | т2 | wо, с–1 | а, м | b, м | R, м | a, град | АО, м | Mz=M*z(t) Н×м | t, с | ОК = s = s (t1) | Т,с |
| кг | ||||||||||||
| –1 | 1,5 | 1,2 | – | pR/6 | –29,6t2 | (5pR/12)t1 | ||||||
| –2 | – | – | 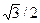
|  t2 t2
| ||||||||
| – | – | – | –120t | ( /4)t12 /4)t12
| ||||||||
| –3 | – | – | 0,4 | 21t | 0,6t1 | |||||||
| 1,5 | 1,5 | – | – | 
| 0,5t1 | 2,5 | ||||||
| –1,25 | 1,5 | – | 2,5 | – | p a /6 | –700t | (5p a /18) t12 | |||||
| –2 | 1,6 | 0,8 | – | (pR/2)t12 | ||||||||
| 1,2 | – | – | p a / 2 | 
| (p a /4) t1 | |||||||
| 1,2 | – | 0,4 | pR/4 | 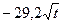
| (3pR/4) t12 | |||||||

| – | – | 
| 
| 
| |||||||
| –1 | – | – | 40t | 0,4 t12 | ||||||||
| –3 | – | – | 50t2 | (p a /3) t1 | ||||||||
| – | – | – | 0,5 | 
| 0,3t1 | |||||||
| – | – | – | 120t | 0,5t1 | ||||||||
| –4 | – | – | 330t2 | (p a /2) t12 | ||||||||
| –5 | 1,2 | – | 0,4 | 0,3 t12 | ||||||||
| –2 | – | – | 1,6 | 0,6 | 69t | 0,6t1 | ||||||
| 0,8 | – | pR/2 | (pR/8)t12 | |||||||||
| 1,5 | – | – | – | –135t | (p a /4) t12 | |||||||
| – | 1,2 | – | p a /6 | –14t2 | (p a /12) t12 | |||||||
| –6 | – | – | – | 
| 
| 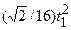
| ||||||
| –1 | 1,6 | 1,2 | 0,6 | – | pR/2 | (pR/2)t12 | ||||||

| – | – | 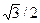
| –210 | (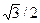 )t1 )t1
| |||||||
| –3 | 0,6 | – | – | 0,2 | 27t2 | 0,4t1 | ||||||
| –5 | – | – | 0,5 | – | 20t | (pR/6)t12 | ||||||
| –4 | 1,5 | – | – | p a /6 | 
| (p a /2) t12 | ||||||
| – | – | –25t | t12 | |||||||||
| –2 | 0,6 | – | – | – | 0,1 | 5,6t | 0,4t1 | |||||
| 0,6 | – | 0,6 | – | 
| (5pR/6)t1 | |||||||
| 1,6 | 1,2 | – | – | 1,6 | 652t | 0,2 t12 |
Примечание. Знак минус перед Мz и w соответствует вращению по направлению вращения часовой стрелки, если смотреть со стороны положительного направления оси z.
Таблица. «Осевые моменты инерции однородных пластин»



Дата добавления: 2015-10-29; просмотров: 114 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение задачи | | | Пример решения Задачи 3 |