Пример решения Задачи 3

Дано: m ₁ = 200 кг; m ₂ = 80 кг; M_z = 592 t Н×м; w₀= – 2 рад/с; АО = 0,8 м;

R = 2,4 м; а = 1,2 м; t = t = 4 c; ОК = s = 0,5 t₁² м; t ₁ = Т = 2 с.

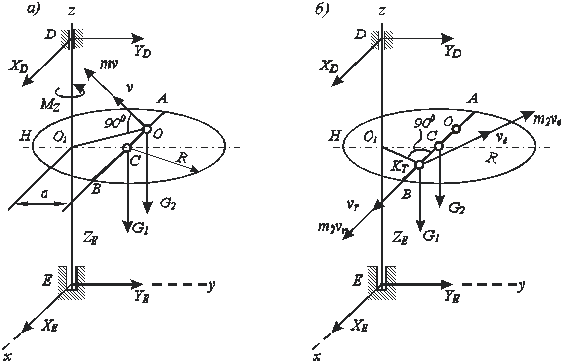
Определить w_t и w_Т, считая тело Н однородной круглой пластинкой. Решение. К решению задачи применим теорему об изменении кинетического момента механической системы, выраженную уравнением

,

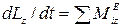где L_z кинетический момент системы, состоящей вданном случае из тела Н, и точки К, относительно оси z; 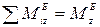– главный момент внешних сил, приложенных к системе, относительно оси z.

На систему за время от t = 0 до t = t действуют силы: вес G₁ тела H, вес G₂ точки К, пара сил с моментом М_z и реакции подпятника и подшипника (рис. а).

Предположим, что вращение тела Н происходит против вращения часовой стрелки, если смотреть со стороны положительного направления оси z; будем считать это направление положительным при определении знаков кинетических моментов.

Найдем выражение кинетического момента L_z системы, который скла­дывается из кинетического момента тела J_z wи момента количества дви­жения точки К, находящейся в точке О тела Н и имеющей скорость v = w× O₁O:

m₂v × O₁O = m₂ w× O₁O².

Таким образом,

L _z = J_z w+ m₂ w× O₁O²= (J_z+ m₂ × O₁O²) w

Главный момент внешних сил равен вращающему моменту М_z, так как другие силы момента относительно оси z не создают.

Уравнение, выражающее теорему об изменении кинетического момента, примет вид

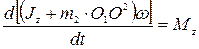(1)

где М_z = ct (с = 592 Н×м/с).

Разделим в уравнении (1) переменные и проинтегрируем левую и правую части уравнения:

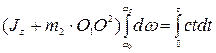
Тогда

(J_z + m ₂ × O ₁ O ²)(w_t– w₀) = ct²/2. (2)

Найдем числовые значения входящих в уравнение (2) величин.

Момент инерции тела Н относительно оси z найдем, используя теорему о зависимости между моментами инерции относительно параллельных осей:

J_z = J_zС+m ₁ a ²,

где J_zC - момент инерции тела H однородной круглой пластинки относительно вертикальной оси, проходящей через центр масс тела параллельно оси z:

J_zC=m ₁ R ² / 2.

Тогда

J_z=m ₁ R ² / 2 + m ₁ a ²,

т. е.

J_z = 864 кг × м².

Из чертежа (рис. 4, б) находим

(O ₁ O)= (ОС)² + (О ₁ С)², или (О ₁ О)² = 4 м²,

поэтому

J_z + m ₂ × O ₁ O ² = 864+ 80×4= 1184 кг×м².

Таким образом, из уравнения (2)

1184 [w_t – (– 2)] = 592 × 4²/2

имеем

w_t = 2 рад/с.

После прекращения действия момента М_z тело H вращается по инер­ции с угловой скоростью w_t; при этом к системе приложены силы G ₁, G ₂, реакции подпятника и подшипника (рис. б).

Те же внешние силы действуют на систему и в течение промежутка времени от t ₁= 0 до t ₁= Т при движении самоходной тележки.

Уравнение, выражающее теорему об изменении кинетического момента системы, имеет для этого периода времени вид

d L_z/ d t = 0,

т. е.

L_z = const.

Определим значения кинетических моментов L_{z 0}при t ₁ = 0 и L_{z t}при t ₁=T и приравняем эти значения.

L_{z 0}= (J_z + m ₂ × O ₁ O ²)w_t = 2368 кг × м²/с.

При t ₁ > 0 скорость точки К складывается из относительной скорости v_r отношению к телу H и переносной скорости v_e в движении вместе с телом Н. Поэтому для t ₁=T покажем два вектора количества движения точк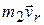и: и .

Для t ₁=T

L_zT = J ₂w_T + m ₂w_T(О₁К)² + m ₂ v_r × O ₁ C.

Найдем

(О ₁ К_Т) ² = (O ₁ С)² + (СК _Т)²,.

где

СК_Т = ОК_Т – ОС, ОК_Т = s_{t 1=T} = 0,5 Т ² = 0,5 × 2² = 2 м,

т.е. СК_Т = 2 – 1,6 = 0,4 м, (О ₁ К_Т)²= 1,2² + 0,4² = 1,6 м²

Относительная скорость

v_r, = d s /d t = t ₁,

при t ₁ = Т = 2 с.

v_r = 2 м/с;

Поэтому

L_zT = 864w_T + 80w_T –1,6 – 80 × 2 × 1,2 = 992w_T - 192.

Приравнивая L_{z 0} и L_zT: 2368 = 992w_T - 192, находим w_T = 2,59

5. Задача 4. «Применение теоремы об изменении кинетической энергии к изучению движения механической системы»

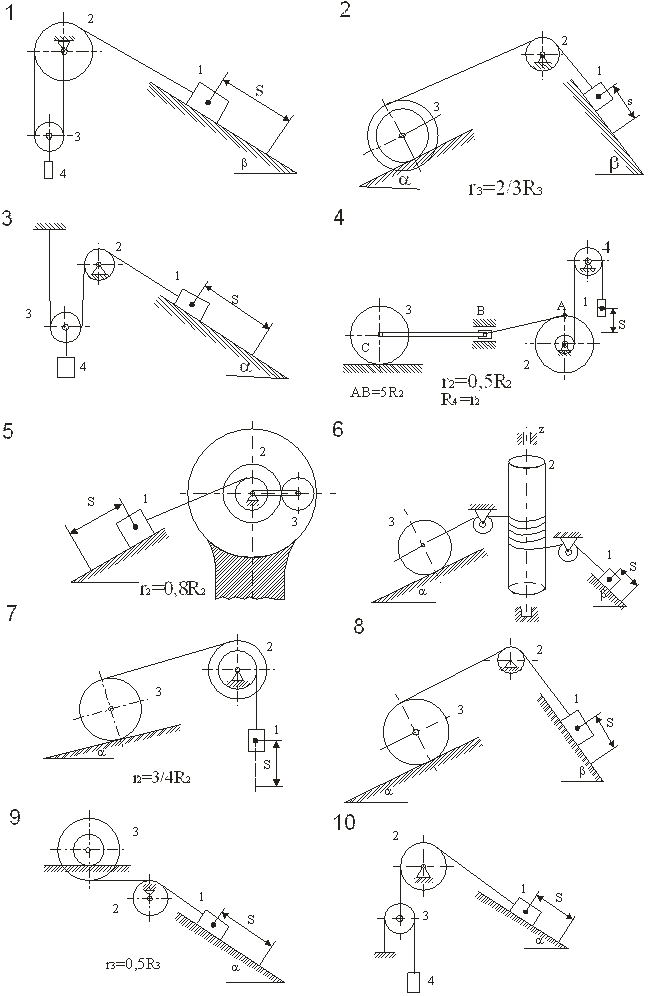
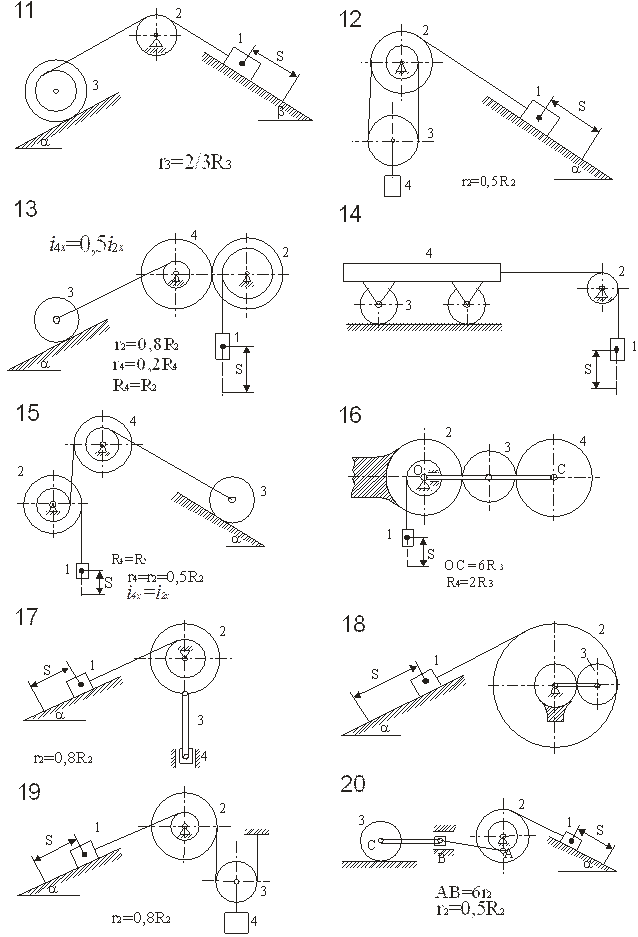
Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рисунках. Учитывая трение скольжения тела 1(варианты 1 – 3, 5, 6, 8 – 12,17 – 23, 28 – 30) и сопротивление качению тела 3, катящегося без скольжения (варианты 2, 4, 6 – 9, 11, 13 – 15, 20, 21, 24, 27, 29), определить скорость тела 1в тот момент, когда пройденный им путь станет равным s.

Другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, пренебречь.

В задании приняты следующие обозначения: т₁ т₂ т₃ т, ₄ – массы тел 1,2,3,4; R₂, r₂, R₃,r ₃ — радиусы больших и малых окружностей; i _2x, i _3x радиусы инерции тел 2 и 3 относительно горизонтальных осей, проходящие через их центры тяжести; a, b – углы наклона плоскостей к горизонту; f – коэффициент трения скольжения; d – коэффициент трения качения.

Необходимые для решения данные приведены в табл. Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами.

Наклонные участки нитей параллельны соответствующим наклонным плоскостям.

№

m1

m2

m3

m4

R2

R3

i2x

i3x

a

b

f

d,см

S,м

Примечание

Кг

см

см

Град

m

4m

1/5m

4/3m

–

–

–

–

–

0,1

–

m

1/2m

1/3m

–

–

–

0,22

0,2

m

m

1/10m

m

–

–

–

–

–

0,1

–

m

2m

40m

m

–

–

–

–

0,3

0,1p

Массами звеньев AB, BC и ползуна B пренебречь

m

2m

m

–

–

–

0,12

–

0,28p

Массой водила пренебречь

m

3m

m

–

–

–

–

0,1

0.28

1,5

m

2m

2m

–

–-

–

–

0,2

m

1/2m

1/3m

–

–

–

–

0,15

0.2

1,75

m

2m

9m

–

–

–

–

0,12

0,25

1,5

m

1/4m

1/4m

1/5m

–

–

–

–

–

0,1

–

m

1/2m

1/4m

–

–

–

0,17

0,2

2,5

m

1/2m

1/5m

m

–

–

–

0,2

–

2,5

m

2m

5m

2m

–

–

–

0,24

m

1/2m

5m

4m

–

–

–

–

–

–

0,2

Массы каждого из 4 колес одинаковы

m

1/2m

4m

1/2m

–

–

–

0,25

1,5

m

1/10m

1/20m

1/10m

–

–

–

–

–

–

0,05p

Массой водила пренебречь

m

1/4m

1/5m

1/10m

–

–

–

0,1

–

0,16p

Шатун 3 рассматривать как тонкий однородный стержень

m

3m

m

–

–

–

0,15

–

0,2p

Массой водила пренебречь

m

1/3m

1/10m

m

–

–

–

0,15

–

1,5

m

2m

20m

–

–

–

0,1

0,2

0,2p

Массами звеньев AB и BC и ползуном B пренебречь

m

m

2m

–

–

0,2

0,32

0,2p

m

½m

¼m

–

–

–

–

0.17

–

0,1p

Массой водила пренебречь

m

m

1/10m

4/5m

–

–

–

0,1

–

m

3m

20m

–

–

–

–

–

0,6

0,08p

Массами звеньев AB, BC и ползуном B пренебречь

m

1/3m

1/4m

–

–

–

–

–

–

–

0,04p

Массой водила пренебречь

m

1/2m

m

1/3m

–

–

–

–

–

–

0,6p

Массы и моменты инерции блоков 2 и 5 одинаковы

m

m

6m

1/2m

–

–

–

0,2

m

2m

3m

–

–

–

–

0,10

–

0,1p

Шатун 3 рассматривать как тонкий однородный стержень

m

1/4m

1/8m

–

–

–

–

0,20

0,20

2,4

m

1/2m

3/10m

3/2m

–

0,12

–

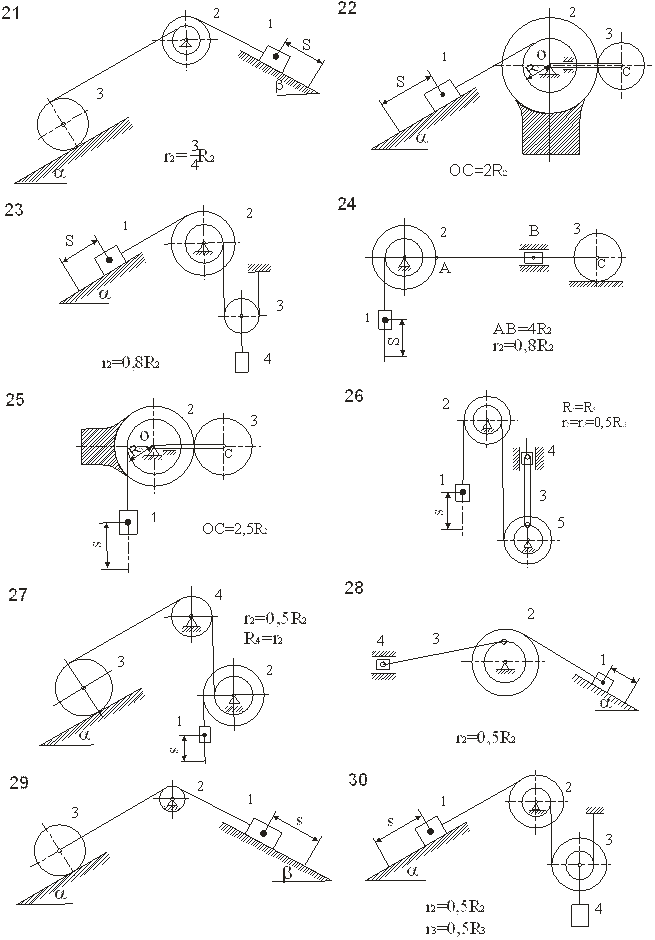
Дата добавления: 2015-10-29