Решение различных систем уравнений, неравенств, уравнений и неравенств

Основные операции

Сложение: a+b

Вычитание: a-b

Умножение: a*b

Деление: a/b

Возведение в степень: a^b

Примеры

314+278; 314-278; 314*278; 314^278;

(a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).

Знаки сравнения

Меньше <: <

Больше >: >

Равно =: = или ==

Меньше или равно?: =<

Больше или равно?: >=

Логические символы

И : &&

ИЛИ : ||

НЕ :!

Основные константы

Число : Pi

Число 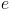: E

Бесконечность : Infinity

Основные функции

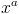: x^a

: Sqrt[x] либо (х)^1/2

: x^(1/n)

: a^x

: Log[a,x]

: Log[x]

: cos[x] или Cos[x]

: sin[x] или Sin[x]

: tan[x] или Tan[x]

: cot[x] или Cot[x]

: sec[x] или Sec[x]

: csc[x] или Csc[x]

: ArcCos[x]

: ArcSin[x]

: ArcTan[x]

: ArcCot[x]

: ArcSec[x]

: ArcCsc[x]

: cosh[x] или Cosh[x]

: sinh[x] или Sinh[x]

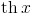: tanh[x] или Tanh[x]

: coth[x] или Coth[x]

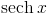: sech[x] или Sech[x]

: csch[x] или Csch[x]

: ArcCosh[x]

: ArcSinh[x]

: ArcTanh[x]

: ArcCoth[x]

: ArcSech[x]

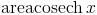: ArcCsch[x]

Решение уравнений

Чтобы получить решение уравнения вида достаточно записать в строке Wolfram|Alpha: f[x]=0, при этом Вы получите некоторую дополнительную информацию, которая генерируется автоматически. Если же Вам необходимо только решение, то необходимо ввести: Solve[f[x]=0, x].

Примеры

Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;

Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;

Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.

Если Ваше уравнение содержит несколько переменных, то запись: f[x,y,...,z]=0 даст весьма разнообразный набор сведений, таких ка решение в целых числах, частные производные функции и т. д. Чтобы получить решение уравнения вида по какой-либо одной из переменных нужно написать в строке: Solve[f[x,y,...,z]=0,j], где 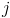— интересующая Вас переменная.

Примеры

Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];

x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];

x+y+z+t+p+q=9.

Решение неравенств

Решение в Wolfram Alpha неравенств типа , полностью аналогично решению уравнения .

Нужно написать в строке WolframAlpha: f[x]>0 или f[x]>=0 или Solve[f[x]>0, x] или Solve[f[x]?0,x].

Примеры

Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];

x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].

Если Ваше неравенство содержит несколько переменных, то запись: f[x,y,...,z]>0 или f[x,y,...,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x,y,...,z]>0,j] или Solve[f[x,y,...,z]>=0,j], где 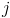— интересующая Вас переменная.

Примеры

Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];

x^2+y^2-5<0 или Solve[x^2+y^2-5<0,x] или Solve[x^2+y^2-5<0,y];

x+y+z+t+p+q>=9.

Решение различных систем уравнений, неравенств, уравнений и неравенств

Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом "И", который в Wolfram Alpha имеет вид: &&.

Примеры

x^2+y^2==9&&x+y=1;

x+y+z+p==1&&x+y-2z+3p=2&&x+y-p=-3;

Sin[x+y]+Cos[x+y]==Sqrt[3]/4&&x+y^2=1;

Log[x+5]=0&&x+y+z<1.

Дата добавления: 2015-10-26