Построение графиков функций

Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида , так и вида .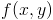

Для того, чтобы построить график функции на отрезке 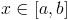нужно написать в строке Wolfram Alpha: Plot[f[x],{x,a,b}]. Если Вы хотите, чтобы диапазон изменения ординаты был конкретным, например 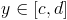, нужно ввести: Plot[f[x],{x,a,b},{y,c,d}].

Примеры

Plot[x^2+x+2, {x,-1,1}];

Plot[x^2+x+2, {x,-1,1},{y,-1,5}];

Plot[Sin[x]^x, {x,-Pi,E}];

Plot[Sin[x]^x, {x,-Pi,E},{y,0,1}].

Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их используя союз "И": Plot[f[x]&&g[x]&&h[x]&&...&&t[t],{x,a,b}].

Примеры

Plot[x&&x^2&&x^3, {x,-1,1},{y,-1,1}];

Plot[Sin[x]&&Sin[5x]&&Sin[10x]&&Sin[15x], {x,-5,5}].

Для того, чтобы построить график функции 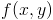на прямоугольнике нужно написать в строке Wolfram Alpha: Plot[f[x,y],{x,a,b},{y,c,d}]. К сожалению, диапазон изменения аппликаты 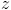пока что нельзя сделать конкретным. Тем не менее, интересно отметить, что при построении графика функции 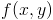Вы получите не только поверхность, которую она определяет, но и "контурную карту" поверхности (линии уровня).

Примеры

Plot[Sin[x^2+y^2],{x,-1,-0.5},{y,-2,2}];

Plot[xy,{x,-4,4},{y,-4,4}].

Математический анализ

Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.

Пределы

Для того, чтобы найти предел последовательности 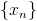нужно написать в строке Wolfram Alpha: Limit[x_n, n -> Infinity].

Примеры

Limit[n^2/(n^2 + 2*n), n -> Infinity];

Limit[(1+1/n)^n, n -> Infinity].

Найти предел функции при 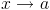можно совершенно аналогично: Limit[f[x], x -> a].

Примеры

Limit[Sin[x]/x, x -> 0];

Limit[(1-x)/(1+x), x -> -1].

Производные

Для того, чтобы найти производную функции нужно написать в строке WolframAlpha: D[f[x], x]. Если Вам требуется найти производную n-го порядка, то следует написать: D[f[x], {x,n}]. В том случае, если Вам требуется найти частную производную функции напишите в окне гаджета: D[f[x,y,z,...,t], j], где 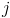— интересующая Вас переменная. Если нужно найти частную производную по некоторой переменной порядка n, то следует ввести: D[f[x,y,z,...,t], {j,n}], где 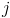означает тоже, что и Выше.

Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на "Show Steps" в правом верхнем углу выдаваемого ей ответа.

Примеры

D[x*E^x, x];

D[x^2*E^x, {x,17}];

D[x^2y^2Sin[x+y], x];

D[x^2y^2Sin[x+y], y],

D[x/(x+y^2), {x,6}].

Интегралы

Для того, чтобы найти неопределенный интеграл от функции нужно написать в строке WolframAlpha: Integrate[f[x], x]. Найти определенный интеграл так же просто: Integrate[f[x], {x, a, b}].

Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на "Show Steps" в правом верхнем углу выдаваемого ей ответа.

Примеры

Integrate[Sin[x]/x^2, x];

Integrate[x^10*ArcSin[x], x];

Integrate[(x+Sin[x])/x, {x,1,100}];

Integrate[Log[x^2+1]/x^5, {x,1,Infinity}].

Дата добавления: 2015-10-26