
Читайте также:
|
Делегати можуть також використовуватися в якості параметрів інших методів. Проілюструємо це на прикладі програмної реалізації наступної математичної задачі. Потрібно знайти корінь рівняння  на відрізку
на відрізку  з точністю
з точністю  (точність за функціоналом), тобто потрібно знайти точку
(точність за функціоналом), тобто потрібно знайти точку  , для якої виконується нерівність
, для якої виконується нерівність 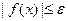 .
.
Для розв’язання цієї задачі існує цілий ряд різних методів, найвідомішими з яких є метод поділу відрізку навпіл, метод хорд та метод дотичних.
Для застосування цих методів необхідно, щоб:
1) функція 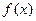 була неперервною;
була неперервною;
2) значення функції 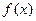 на кінцях відрізка мали протилежні знаки (тоді гарантується, що корінь на відрізку існує);
на кінцях відрізка мали протилежні знаки (тоді гарантується, що корінь на відрізку існує);
3) для методу дотичних обов’язково потрібно, щоб функція f(x) була опуклою або угнутою на відрізку.
Усі три методи знаходження кореня ґрунтуються на єдиній ітеративній процедурі, кожна ітерація якої зводиться до виконання наступних кроків.
Крок 1. За деяким правилом вибирається точка (наближення) з 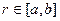 .
Крок 2. Для подальшого розгляду вибирається один з відрізків .
Крок 2. Для подальшого розгляду вибирається один з відрізків 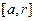 або або  , на якому далі буде проводитися пошук кореня. Очевидно, що має бути вибраний той із відрізків, на кінцях якого функція приймає значення різних знаків. Тобто:
якщо , на якому далі буде проводитися пошук кореня. Очевидно, що має бути вибраний той із відрізків, на кінцях якого функція приймає значення різних знаків. Тобто:
якщо 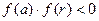 , то , то  , інакше , інакше 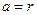 .
Крок 3. Якщо на новому відрізку .
Крок 3. Якщо на новому відрізку  , то , то  – наближене значення кореня. Якщо ж – наближене значення кореня. Якщо ж  , то , то 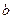 – наближене значення кореня. – наближене значення кореня.
|
Відмінності методу поділу відрізку навпіл, методу хорд та методу дотичних полягають у реалізації першого кроку кожної ітерації зазначеної процедури. Так, метод поділу відрізку навпіл вибирає в якості наближення 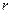 середину відрізку
середину відрізку  ; метод хорд – точку перетину відрізку, що з’єднує точки
; метод хорд – точку перетину відрізку, що з’єднує точки  та
та  , з віссю абсцис; метод дотичних – точку перетину однієї з дотичних до графіка функції
, з віссю абсцис; метод дотичних – точку перетину однієї з дотичних до графіка функції 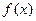 , побудованих у точках
, побудованих у точках  або
або 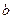 , із віссю абсцис (вибирається та із точок перетину, яка належить відрізку [a, b]).
, із віссю абсцис (вибирається та із точок перетину, яка належить відрізку [a, b]).
На мал. 2.1 зображені варіанти вибору наступного відрізку, на якому буде здійснений подальший пошук кореня, коли точка 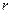 визначається методом хорд. На мал. 2.1, а) наведена зміна лівого кінця відрізку (на наступній ітерації точку
визначається методом хорд. На мал. 2.1, а) наведена зміна лівого кінця відрізку (на наступній ітерації точку  перенесемо в точку
перенесемо в точку 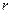 ), на мал. 2.1, б) – правого (точку
), на мал. 2.1, б) – правого (точку 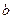 перенесемо в точку
перенесемо в точку 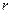 ).
).

Мал. 2.1. Демонстрація однієї ітерації методу хорд.
Створимо клас Solver, який буде розв’язувати рівняння. Цей клас буде містити тільки один відкритий статичний метод GetRoot() для визначення кореня рівняння. Інші методи – метод визначення точки середини відрізка (MidPoint()) та точки перетну хорди (SecantPoint()), будуть закритими, тобто будуть грати допоміжну роль.
Така структура класу передбачає використання делегатів у якості параметрів у двох випадках. По-перше, будемо передавати у метод GetRoot() інструкцію (вказівку) як обраховувати функцію 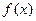 з допомогою параметра f типу ElementaryFunction. По-друге, як вже було сказано, методи пошуку кореня базуються на основі єдиної процедури, яка відрізняється тільки одним кроком – вибору точки, яка розбиває відрізок на два. Інформацію про метод вибору точки будемо передавати у метод GetRoot() за допомогою параметру method наступного типу:
з допомогою параметра f типу ElementaryFunction. По-друге, як вже було сказано, методи пошуку кореня базуються на основі єдиної процедури, яка відрізняється тільки одним кроком – вибору точки, яка розбиває відрізок на два. Інформацію про метод вибору точки будемо передавати у метод GetRoot() за допомогою параметру method наступного типу:
| public delegate double GetApproximation(ElementaryFunction f, double a, double b); |
Таким чином, отримуємо наступну програмну реалізацію класу Solver:
| public class Solver { // метод, що повертає точку середини відрізку double MidPoint(ElementaryFunction f, double a, double b) { return (a + b) / 2; } // метод, що повертає точку перетину хорди з віссю ОХ public static double SecantPoint(ElementaryFunction f, double a, double b) { return a - f(a) * (b - a) / (f(b) - f(a)); } // метод розв'язання рівняння // параметр 1 -- делегат функції, яка визначає рівняння // параметри 2,3 -- кінці відрізку // параметр 4 -- точність // параметр 5 -- делегат методу вибору точки // параметр 6 -- через нього повертається кількість ітерацій, яку здійснив методу для // досягнення заданої точності // параметр 7 -- обмеження на кількість ітерацій public static double GetRoot(ElementaryFunction f, double a, double b, double eps, GetApproximation method, out int n, int nmax = int.MaxValue) { // корінь гарантовано існує, якщо на кінцях відрізку функція приймає значенння // різних знаків if (f(a) * f(b) > 0) throw new Exception("Можливо, коренів на цьому відрізку не існує."); if (a > b) throw new Exception("Не правильно задані кінці відрізку."); n = 0; while (n <= nmax) { n++; // крок1: визначення точки поділу відрізку - виклик делегата double r = method(f, a, b); // крок2: вибір наступного відрізку if (f(a) * f(r) < 0) b = r; else a = r; // крок3: вибір наближеного значення кореня if (Math.Abs(f(a)) <= eps) return a; if (Math.Abs(f(b)) <= eps) return b; } throw new Exception("Не вдалося знайти корінь рівняння при заданих аргументах!"); } } |
Використання розробленого класу для наближеного розв’язання рівняння 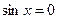 може бути таким:
може бути таким:
Дата добавления: 2015-10-26; просмотров: 135 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Організація роботи із файлами даних стандарту XML | | | Події: створення та обробка |