Агрегація та композиція

Застосування успадкування є ефективним у тому випадку, якщо розроблювальний клас має подібну структуру та елементи поведінки до деякого іншого класу. У тих випадках, коли успадкування з якихось причин є недоцільним, можна використовувати композицію або агрегацію класів.

Обидва відношення є різновидом відношення «ціле/частина» між об’єктами класів. Відношення «ціле/частина» − вказує на те, що деяка абстракція є частиною (елементом, складовою) іншої більш загальної абстракції, наприклад, «точка − складова множини точок» також «складовими трикутника є три точки (його вершини), що не лежать на одній прямій».

Композицією називається таке відношення між класами, коли об’єкт одного класу (класу-частини) є невід’ємною частиною об’єкта іншого (класу-цілого). Наприклад «вершини трикутника є його невід’ємними складовими». Конкретно, композиція реалізується включенням в клас поля, що є об’єктом іншого класу або масиву таких об’єктів. Такі поля зазвичай називають об’єктними полями. На діаграмі класів композицію зображують лінією із зафарбованим ромбом, що вказує на клас-ціле (клас-композит), у який відбувається включення об’єктних полів (мал. 3). Для більшої інформативності є сенс вказувати над стрілкою кількість об’єктів класу-частини, які включається у кожний об’єкт класу-композиту. При цьому допускається вказувати точне значення або діапазон (мал. 3)

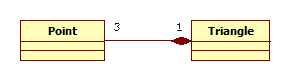
Мал. 3. Приклад діаграми класів, що відповідає композиції класів

Агрегацією або наповненням називають таке відношення між класам, при якому точна кількість об’єктів одного класу (класу-частини), що включаються в інший клас (клас-агрегат), є необмеженою та може мінятися від 0 до досить великих значень. Наприклад «множина точок може бути порожньою, а може містити і достатньо велику кількість точок». На діаграмі класів наповнення зображують аналогічно композиції, але ромб не зафарбовують (мал. 4), позначаючи в такий спосіб менш сильний зв’язок між об’єктами відповідних класів. Кількість об’єктів вказують у вигляді діапазону, наприклад, «0..*» або «1..*», або просто «*», що означає невизначений набір об’єктів.

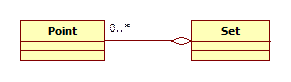
Мал. 4. Приклад діаграми класів, що відповідає агрегації класів

Окрім вже визначених вище, на діаграмі класів показують також відношення асоціації між класами, об’єкти яких обмінюються повідомленнями, але не зв’язані відношеннями композиції або агрегації. Вони позначаються лініями без стрілок. Якщо повідомлення передаються в одну сторону, то напрямок асоціації можна показати стрілкою на кінці. Крім того, асоціації можна дати ім’я, яке в даному контексті називають роллю.

Проілюструємо механізм розробки класів на прикладі класу «Опуклий многокутник». Нагадаємо, що у геометрії многокутник − це проста (без самоперетинів) замкнена ламана, сусідні ланки якої не лежать на одній прямій. А оскільки невід’ємними складовими будь-якої ламаної за визначенням є точки − вершини цієї ламаної, то є сенс говорити про композицію «Опуклий многокутник/Точка». З урахуванням сказаного та вже наявних реалізацій класів «Фігура» та «Точка» діаграма класів (мал. 5) прийме наступний вигляд.

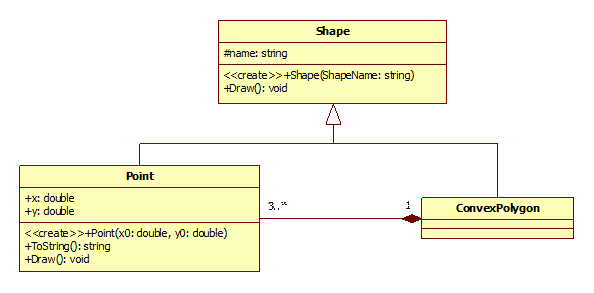
Мал. 5. Діаграма класів геометричних фігур.

Детально розглянемо реалізацію класу «Опуклий многокутник». Даними цього класу є кількість вершин многокутника та вершини многокутника. Їх ми визначимо наступним чином.

public class ConvexPolygon: Shape { //кількість вершин многокутника byte n; //масив точок - вершини многокутника Point[] vertices; }

Конструктор класу відповідає за коректну ініціалізацію полів класу, тому він повинен створювати об’єкти-частини, викликаючи, як правило, конструктори відповідних класів. Так у нашому випадку конструктор буде створювати найпростіший випадок опуклого многокутника − трикутник.

public class ConvexPolygon: Shape { ... //конструктор без параметрів public ConvexPolygon():base("Опуклий многокутник") { n = 3; vertices = new Point[n]; vertices[0] = new Point(0, 0); vertices[1] = new Point(1, 0); vertices[2] = new Point(0, 1); } }

Реалізуємо у класі ConvexPolygon також конструктор з параметрами: для можливості створення об’єктів на основі заданого користувачем набору точок. Коректна реалізація конструктора класу у нашому випадку може бути зведена до задачі побудови опуклої оболонки для заданого набору точок площини.

Опуклою оболонкою деякої заданої множини точок називається перетин всіх випуклих множин, що містять задану множину. Для скінченної множини точок опуклою оболонкою завжди буде опуклий многокутник, всі вершини якого будуть точками вихідної множини. Наша задача полягає у тому, щоб для заданого скінченого набору точок знайти вершини опуклої оболонки цього набору. Серед методів обчислювальної геометрії для розв’язання цієї задачі існує декілька ефективних алгоритмів. Наведемо найбільш просту реалізацію одного з них − алгоритму Джарвіса. Цей алгоритм інколи називають «загортанням подарунку». (див. мал. 6.)

Мал. 6. Графічна інтерпретація алгоритму Джарвіса.

Перебір точок починається із правої нижньої точки 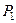, яка апріорі належить опуклій оболонці. Наступною при зазначеному на мал. 2 напрямку обходу буде точка 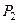. Вона, очевидно володіє тією властивістю, що всі інші точки лежать «лівіше» від вектора 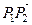. Це означає, що псевдоскалярний добуток векторів 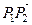та 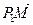є невід’ємним для будь-якої іншої точки 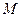нашого набору. Якщо таких точок декілька, то вершиною шуканого многокутника буде та, для якої довжина вектора 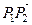максимальна.

Так само поступають і далі. Припустимо, що уже знайдена вершина 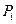опуклої оболонки. Пошук наступної вершини можна здійснювати так. Спочатку можна вважати в якості наступної точки 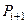будь-яку точку, яка ще не знайдена, окрім першої. Потім, розглядаючи в якості 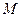всі інші точки та перша, і обчислюється значення псевдоскалярного добутку векторів 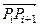та 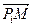за формулою: 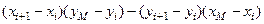. У випадку, коли значення вказаного виразу менше за нуль або ж значення виразу дорівнює нулю і при цьому довжина вектора 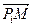більша за довжину вектора 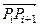, то вважаємо наступною точкою вже точку 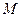та продовжуємо далі перевірку інших точок (як у алгоритмі пошуку найменшого елемента). Продовжуючи цю процедуру, ми на якомусь кроці повернемось до точки 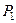. Це буде означати, що опуклу оболонку побудовано.

Програмно реалізуємо описаний алгоритм у вигляді відкритого статичного методу getConvexHull окремого статичного класу CompGeometry. У цьому класі також реалізуємо ряд допоміжних та корисних методів обчислювальної геометрії.

//клас методів обчислювальної геометрії public static class CompGeometry { //метод визначення відстані між двома точками public static double Distance(Point p1, Point p2) { return Math.Sqrt(Math.Pow((p2.x - p1.x), 2) + Math.Pow((p2.y - p1.y), 2)); } //метод визначення відстані від точки до початку координат або довжини радіус-вектора точки public static double Distance(Point p) { return Distance(p, new Point(0,0)); } //метод визначення псевдоскалярного добутку радіус-векорів двох точок public static double WedgeProduct(Point p1, Point p2) { return (p1.x * p2.y - p1.y * p2.x); } //перевантаження методу WedgeProduct для випадку, коли точки визначають кінці двох векторів public static double WedgeProduct(Point p1, Point p2, Point p3, Point p4) { return (p2.x - p1.x) * (p4.y - p3.y) - (p4.x - p3.x) * (p2.y - p1.y); } //метод побудови опуклої оболонки заданого набору точок за алгоритмом Джарвіса public static byte getConvexHull(Point[] p) { //визначаємо кількість точок набору byte n0 = (byte)p.Length; //кількість точок набору, що увійшли до опуклої оболонки byte _n = 0; //шукаємо праву нижню точку byte m = 0; for (byte i = 1; i < n0; i++) if (p[i].y < p[m].y) m = i; else if ((p[i].y == p[m].y) & (p[i].x < p[m].x)) m = i; do { //записуємо знайдену вершину на відповідне місце початку масиву if (m!= _n) { Point tmp = p[m]; p[m] = p[_n]; p[_n] = tmp; } //шукаємо наступну вершину опуклої оболонки m = (byte)((_n + 1) % n0); for (byte j = 0; j < n0; j++) if (j!= m) if ((j == 0) || (j > _n)) if ((WedgeProduct(p[_n], p[m], p[_n], p[j]) < 0) || ((WedgeProduct(p[_n], p[m], p[_n], p[j]) == 0) & (Distance(p[_n], p[m]) < Distance(p[_n], p[j])))) m = j; _n++; } while (m!= 0); return _n; } }

Метод getConvexHull повертає число точок набору, які увійшли до опуклої оболонки, та розташовує їх на початку вихідного масиву у порядку їх визначення.

Тепер маючи як інструмент метод побудова опуклої оболонки скінченної множини точок, можна реалізувати спеціальний конструктор класу ConvexPolygon, який буде робити коректну ініціалізацію полів цього класу на основі заданого користувачем набору точок.

public class ConvexPolygon: Shape { ... //конструктор з параметрами public ConvexPolygon(params Point[] args) : this() { byte newn; if (args.Length < 3) { Console.WriteLine("Недостатня кiлькiсть параметрiв."); Console.WriteLine("Використано конструктор без параметрів."); } else { newn = CompGeometry.getConvexHull(args); if (newn < 3) { Console.WriteLine("Не можна побудувати опуклу оболонку даної множини точок у виглядi многокутника."); Console.WriteLine("Використано конструктор без параметрів."); } else { n = newn; vertices = new Point[n]; vertices = args; } } } }

Перевизначимо віртуальний поліморфний метод Draw базового класу наступним чином.

public class ConvexPolygon: Shape { ... //перевизначення методу зображення базового класу public override void Draw() { Console.WriteLine("{"); Console.WriteLine(" Фiгура - {0}", name); Console.Write(" Вершини: "); for (int i = 0; i < n; i++) Console.Write("{0} ",vertices[i].ToString()); Console.WriteLine("\n }"); } }

Діаграма реалізованих нами класів геометричних фігур зображена на мал. 7.

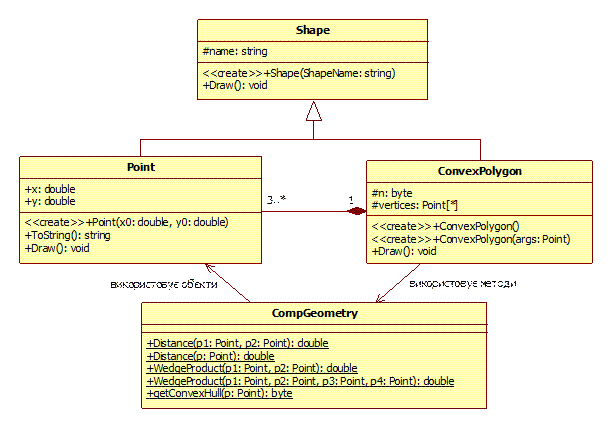
Мал. 7. Діаграма класів геометричних фігур.

На завершення підтеми відмітимо наступні додаткові аспекти зв’язку «ціле/частина».

Об’єкт-частина надає об’єкту-цілому поля та методи. Об’єкти-ціле створюють об’єкти-частини. Викликаючи доступні їм методи та поля об’єктів-частин, вони керують роботою створених об’єктів-частин. Об’єкт-ціле не може змінювати ані поведінку методів об’єкту-частини, ані склад доступних полів та методів, він не може викликати закриті об’єктом-частиною поля та методи класу.

Об’єкт-частина цікавий об’єкту-цілому своєю відкритою частиною, тобто своїм інтерфейсом. Це означає, що при розробці класу об’єкту-цілого їх реалізація, ґрунтується здебільшого тільки на інтерфейсній частині класу об’єкта-частини.

Об’єкт класу може бути об’єктом-частиною для самого себе. Така ситуація характерна для динамічних структур даних. Елемент однозв’язного списку має поле, що представляє елемент однозв’язного списку, елемент двозв’язного списку має два такі поля, вузол двійкового дерева має два поля, що представляють вузли двійкового дерева.

Дата добавления: 2015-10-26