Индексы средних величин

Иногда есть необходимость сопоставлять не всю совокупность, а ее среднее значение (например, средняя заработная плата, средняя цена на овощи).

При сравнении уровня средних величин отчетного и базисного периода получают индекс изменения средней величины, который описывает динамику средних величин. На него оказывают влияние 2 фактора:

1. Изменение самих уровней усредняемого признака индексируемой величины (x, размер стипендии);

2. «Структурные сдвиги» – это изменение долей единиц совокупности с различными значениями признака (количество студентов, которые получают ту или иную стипендию).

Важно выяснить и определить в какой мере на изменение средней величины повлиял первый фактор, а в какой – второй. Изучение совместного действия этих двух факторов на общую динамику среднего уровня осуществляется в статистике с помощью индекса переменного состава.

· Индекс изменения средней величины получается как произведение индексов в неизменной структуре на индекс, учитывающий изменение структуры.

· Индекс переменного состава представляет собой отношение двух взвешенных средних с изменяющимися (переменными) весами, показывающее изменение индексируемой средней величины. Т.к. он меняется и за счет индексируемого показателя, и за счет изменение долей единиц то для любых качественных показателей х индекс переменного состава можно записать в общем виде:

где x 1, x 0 _ уровни усредняемого показателя в отчетном и базисном периодах соответственно; f 1, f 0 _ веса (частоты) осредняемого показателя в отчетном и базисном периодах соответственно.

· Чтобы элиминировать влияние изменения структуры совокупности на динамику средней величины, берут отношение средних взвешенных с одними и теми же весами (как правило, на уровне отчетного периода). Индекс, характеризующий динамику средней величины при одной и той же фиксированной структуре совокупности, носит название индекса постоянного (фиксированного) состава. Индекс постоянного или фиксированного состава используется для того, чтобы исключить влияние изменения структуры совокупности на динамику средних величин и исчисляется в общем виде:

После сокращения на 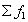формула принимает вид формулы агрегатного индекса качественного показателя:

Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилось среднее значение показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т.е. когда влияние структурного фактора устранено.

· Для измерения влияния только структурных изменений на исследуемый средний показатель исчисляют индекс структурных сдвигов как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчетную структуру, к фактической средней этого показателя в базисном периоде (для избежания эффекта Гершекрона меняем f но не x!):

Между индексами переменного, постоянного составов и индексом структурных сдвигов существует следующая взаимосвязь:

т.е. индекс переменного состава выступает как произведение двух индексов: индекса постоянного состава и индекса структурных сдвигов.

Дата добавления: 2015-10-26