Екзамен.білет № 28 3 страница

1. Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:

Спочатку побудуємо двоїсту задачу: F= y₂+3y₂ (Max)

y₁+ 2y₂ ≤14

-5y₁+3y₂ ≤15

-4y₁ -6y₂ ≤ -24

Відповідно до обмежень будуємо прямі. Далі визначаємо корд. Напрямного вектора (1;3) потім знаходимо точки min(6;0) та max(0.923;6.54).

Будуємо ЦФ:

F(max)= 0.923 +3 * 6.54 =20.5

F(min) = 6

Розв’язки двоїстої задачі відповідають розвязкам прямої

БИЛЕТ № 20

4) Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:

Побудує двоїсту задачу

F(min) = 4y₁-y₂

Y₁+ y₂ ≥ 1

Y₁-y₂ ≥ 8

Y₁ -2y₂ ≥ 10

Точка А(10;0) точка мінімуму

F(min)=40

5) за умов: х₁ +х₂≤6

.

Розв’язування. У даному прикладі множина допустимих розв’язків складається з двох окремих частин, необмежених звер­ху. Цільова функція аналогічно попередньому випадку є колом з центром у точці М (4; 4). Функція Z має два локальних мінімуми: в точці А (), і в точці В ().

Значення функціонала в цих точках однакове і дорівнює:

.

Отже, маємо два альтернатив­ні оптимальні плани.

Билет № 21

4. Визначити (застосовуючи теореми двоїстості й не розв’язуючи задачі симплексним методом), чи оптимальні запропоновані плани задачі лінійного програмування:

а) x =(10;10/3); б) x =(20;10); в) x =(10/ 3;10/3).  

Формуємо двоїсту задачу згідно правил побудови двоїстих задач

Min F = -30y1+10y2

-2y₁+y₂+y₃ ≤2

-3y₁+ y₂ – y₃ ≤3

А) Х = (10;10/3)

Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.

30=30

16.6>10

6.7 > 0

План допустимий і для нього F = 30. Визначимо оптимальний план двоїстої задачі користуючись другою теоремою двоїстості. Оскільки Х1>0, та X2>0 то згідно з другою теоремою двоїстості можна записати перше та друге обмеження рівнянням.

-2y₁+y₂+y₃ ≤2 y1=-1

-3y₁+ y₂ – y₃ ≤3 y2=0

Y3=0

Б) Х = (20;10)

Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.

70≠30

40>10

10≥0

Так як обмеження не виконується дана точка не може бути оптимальним розв’язком нашої задачі.

В) (10/3;10/3)

Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.

16.6<30

10=10

0=0

F=16.6

5) Знайти мінімальне значення функції:

за умов:

.Розв’язування. У даному прикладі множина допустимих розв’язків складається з двох окремих частин, необмежених звер­ху (рис. 8.2). Цільова функція аналогічно попередньому випадку є колом з центром у точці М (4; 4). Функція Z має два локальних мінімуми: в точці А (), і в точці В ().

Значення функціонала в цих точках однакове і дорівнює:

.

Отже, маємо два альтернатив­ні оптимальні плани.

Билет 22

1. Визначити (застосовуючи теореми двоїстості й не розв’язуючи задачі симплексним методом), чи оптимальні запропоновані плани задачі лінійного програмування:

а) x =(1;1/3;1); б) x =(2;1;0); в) x =(1/8;0;13/8).  

Формуємо двоїсту задачу згідно правил побудови двоїстих задач

Min F = 5y1+2y2

А) Х = (1;1/3;1)

Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.

Так як обмеження не виконується дана точка не може бути оптимальним розв’язком нашої задачі.

Б) Х = (2;1;0)

Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.

План допустимий і для нього F =-4. Визначемо оптимальний план двоїстої задачі користуючись другою теоремою двоїстості. Оскільки Х1>0 та Х2>0 то згідно з другою теоремою двоїстості можна записати перше та друге обмеження рівнянням.

→

Підставимо отримані значення в третє обмеження та визначимо чи задовольняє вона наше обмеження.

3*(-2,15)+3,38≥6

-3,07≥8 Як бачимо обмеження не виконується отже дана точка не може бути оптимальним розв’язком нашої задачі.

В) (1/8;0;13/8

→

План допустимий і для нього F =10,75. Визначемо оптимальний план двоїстої задачі користуючись другою теоремою двоїстості. Оскільки Х1>0 та Х3>0 то згідно з другою теоремою двоїстості можна записати перше та третє обмеження рівнянням.

→

Підставивши отримані значення в наше друге обмеження отримуємо 1,75>-20 Отже третя точка є нашим оптимальним планом.

2. Розв’язати графічним методом задачу нелінійного програмування; знайти глобальні екстремуми:

.

Будуємо прямі на графіку які відп. нашим обмеж. та ЦФ, яка буде представляти собою кола різного радіуса при чому .

Точка мінімуму буде в точці А а точка максимуму в точці В так як показник цільової функції при координатах точки більше ніж при координатах точки С.

БИЛЕТ № 23

1. Розв’язати транспортну задачу:

ai = (8; 10; 5); bj = (5; 5; 10);

	B1	B2	B3	B4
A1
A2
A3

	B1	B2	B3	B4
A1
A2
A3

Z= 5*0 + 3*2 + 2*2 + 8*3 + 2*5 + 3*50 = 6+4+24+10+150=194

Рішення 1 рішення 2

	B1	B2	B3	B4
A1		-1	+1
A2		+1	-1
A3

	B1	B2	B3	B4
A1		-1		+1
A2		+1	-1
A3			+1	-1

Рішення 3

	B1	B2	B3	B4
A1	-1	+1
A2	+1	-1
A3

Ріш 4	B1	B2	B3	B4
A1
A2			-1	+1
A3			+1	-1

Рішення 5 Ришення 6

	B1	B2	B3	B4
A1	-1	+1
A2		-1	+1
A3	+1		-1

	B1	B2	B3	B4
A1
A2		-1	+1
A3		+1	-1

1) 50-2+1-3+5-50 = 48-2-45 = 1

2) 2-0+2-1 = 3

3) 1-2+1-3 = -1 – 2 = -3

4) 50-3+5-50 = 47-45 = 2

5) 2-0+3-1+2-5 = 2+2-3 = 1

6) 3-1+4-5 = 2-1 = 1

№1

	B1	B2	B3	B4
A1			-1	+1
A2
A3			+1	-1

1) 50-1+5-50 = 49-45 =4

№2

	B1	B2	B3	B4
A1	-1	+1
A2	+1	-1
A3

2)2-0+2-1 =3

№3

	B1	B2	B3	B4
A1
A2			-1	+1
A3			+1	-1

1) 50-3+5-50 = 47 – 45 =2

№4

	B1	B2	B3	B4
A1	-1	+1
A2		-1	+1
A3	+1		-1

2) 2-0+3-1+2-5=2+2-3=1

№5

	B1	B2	B3	B4
A1
A2		-1	+1
A3		+1	-1

3) 3-1+4-5 = 2-1 = 1

Z = 4+1+3+21+10+150 =24+5+10+150 = 189

2. Розв’язати графічним методом задачу нелінійного програмування; знайти глобальні екстремуми:

Будуємо прямі на графіку які відповідають нашим обмеженням та цільову функцію, яка буде представляти собою кола різного радіуса при чому .

Точка мінімуму буде в точці О а точка максимуму в точці В(6;0) так як показник цільової функції при координатах точки більше ніж при координатах точки С(0;6).

БИЛЕТ № 24

1. Розв’язати транспортну задачу:

ai = (8; 7; 6); bj = (7; 10; 6);

.

	B1	B2	B3
A1
A2
A3

	B1	B2	B3
A1
A2
A3
А4

	B1	B2	B3
A1
A2
A3
А4

Z=5+21+4+0+100 = 130

№ 1

	B1	B2	B3
A1		-1	+1
A2
A3		+1	-1
А4

1) 2-5+3-4 = -3 – 1 =-4

№ 2

	B1	B2	B3
A1	-1	+1
A2	+1	-1
A3
А4

2) 5-0+2-3 = 4

№ 3

	B1	B2	B3
A1
A2		-1	+1
A3		+1	-1
А4

3) 4-3+2-0 = 3

№ 4

	B1	B2	B3
A1	-1	+1
A2
A3	+1	-1
А4

4) 5-0+1-2 = 4

№ 5

	B1	B2	B3
A1	-1	+1
A2
A3		-1	+1
А4	+1		-1

5) 5 – 0+0-2+50-50=5+12-50 = 3

№ 6

	B1	B2	B3
A1
A2
A3		-1	+1
А4		+1	-1

6) 0 -4+50-50=-2

7)

	B1	B2	B3
A1
A2
A3
А4

№1

	B1	B2	B3
A1		+1	-1
A2
A3		-1	+1
А4

1) 5-2 -2 = 1
№2

	B1	B2	B3
A1	-1		+1
A2	+1	-1
A3		+1	-1
А4

2) 2-0+2-3+2-0 =3

№3

	B1	B2	B3
A1
A2		-1	+1
A3		+1	-1
А4

3) 4-3+2-0 =3

№4

	B1	B2	B3
A1	-1		+1
A2
A3	+1		-1
А4

4) 2-0+1-0= 3

№5

	B1	B2	B3
A1	-1		+1
A2
A3
А4	+1		-1

5) 2-0 + 50 -50 =2

6) Z= 7*0+2+21+4+0=50+50=127

2 ) Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

, .

L(x1,x2,£) = +£*(x1+x2-2)

£

£

.

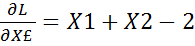£=-4X1-X2-2 -4X1-X2-2=-X1-2X2+4

£= -X1-2X2+4 -4X1+X1-X2+2X2=2+4

-3X1+X2=6

X2=6+3X1

X1+6+3X1-2=0

4X1+4=0

X1=-1

X2=3

H=

Точки X=(-1; 3) є точкою max

Z= 2+3+9-2-12=1+9-2-12=15+9 = -6

Білет №25

1. Розв’язати транспортну задачу:

ai = (10; 20; 40); bj = (30; 10; 60);	.

де с_ij — вартість перевезення одиниці продукції від і -го постачальника до j -го споживача,

а_i — запаси продукції і -го постачальника; b_j — попит на продукцію j -го спо­живача.

Перевіряємо нашу задачу на збалансованість. Оскільки сумарний попит перевищує запаси, вводимо фіктивний склад:

Формуємо опорний план за методом північно-західного кута.

Значення функції: Z = 10*1+20*2+10*6+30*8+30*10=650

За методом Степінг-Стоун перебираємо всі допустимі плани задачі, формуючи цикли та здійснюючи перебір пустих клітинок у кожному плані. Приклад:

10 -	+
+	10 -

σ = 3-1+3-6=-1

Якщо значення сігма менше нуля, то існує кращий план і наявний можна поліпшити, за алгоритмом симплекс методу переходимо до нового плану. Процедуру повторюємо доти поки не знайдемо оптимальний план.

У даному випадку на 3-му етапі знаходимо оптимальний план:

Z=10*3+20*5+30*3+10*8+10*30=600

2. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

,.

Вводимо в цільову функцію множник лагранжа:

Z(x1,x3,λ)= x1²+x2²-2x1+3x2+4+ λ(3-x1-2x2)

Знаходимо похідні:

Дата добавления: 2015-10-31