Екзамен.білет № 28 2 страница

x1=0 x2=10 x3=16 ЦФ=26

3. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

, .

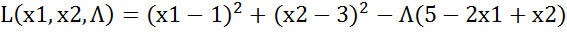
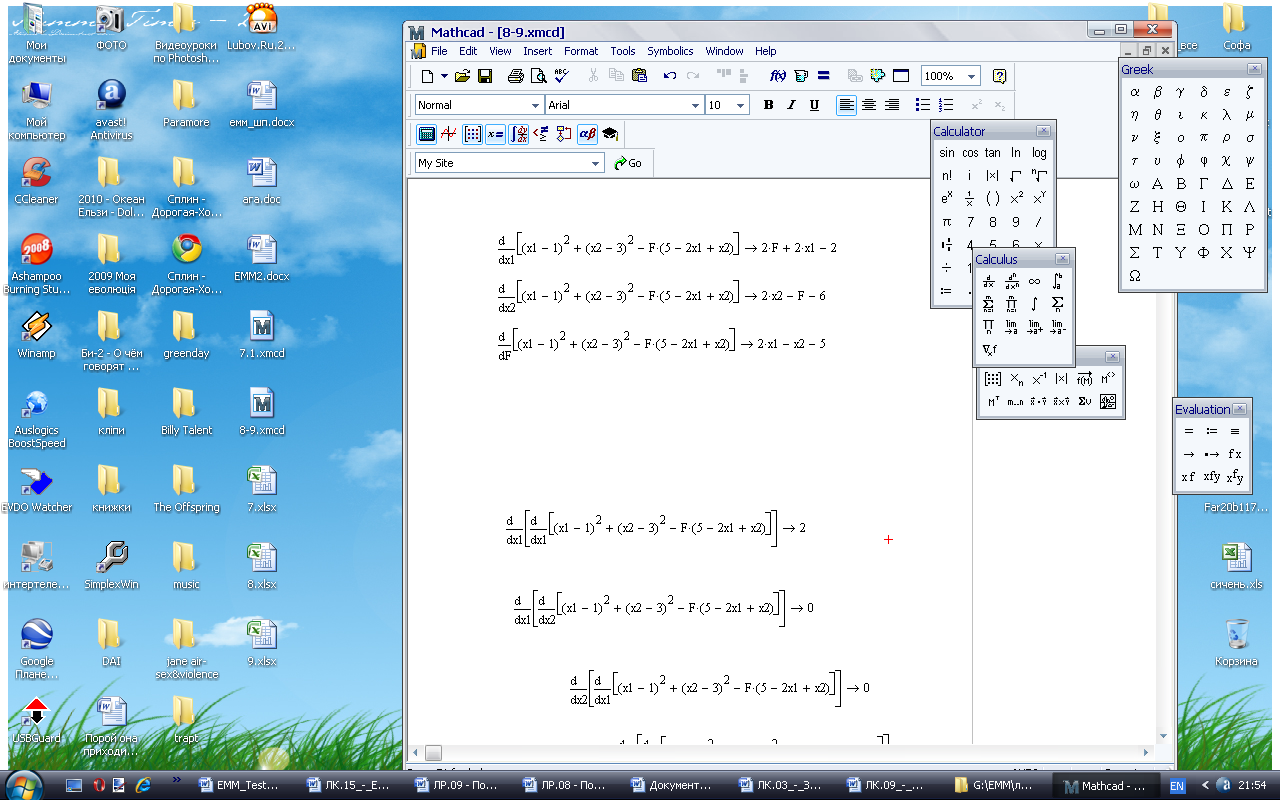
Прирівнюємо до нуля, розв’язуємо систему, з неї отримуємо х1=3,4; х2=1,8; 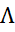=-2,4

Записуємо матрицю Гессе

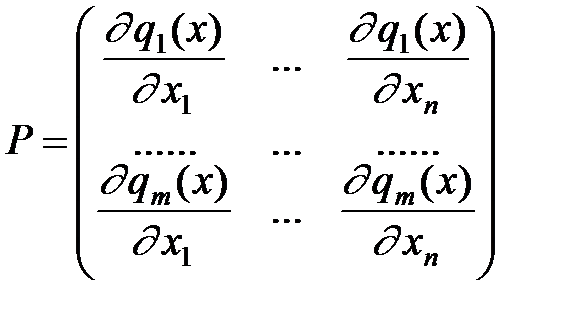
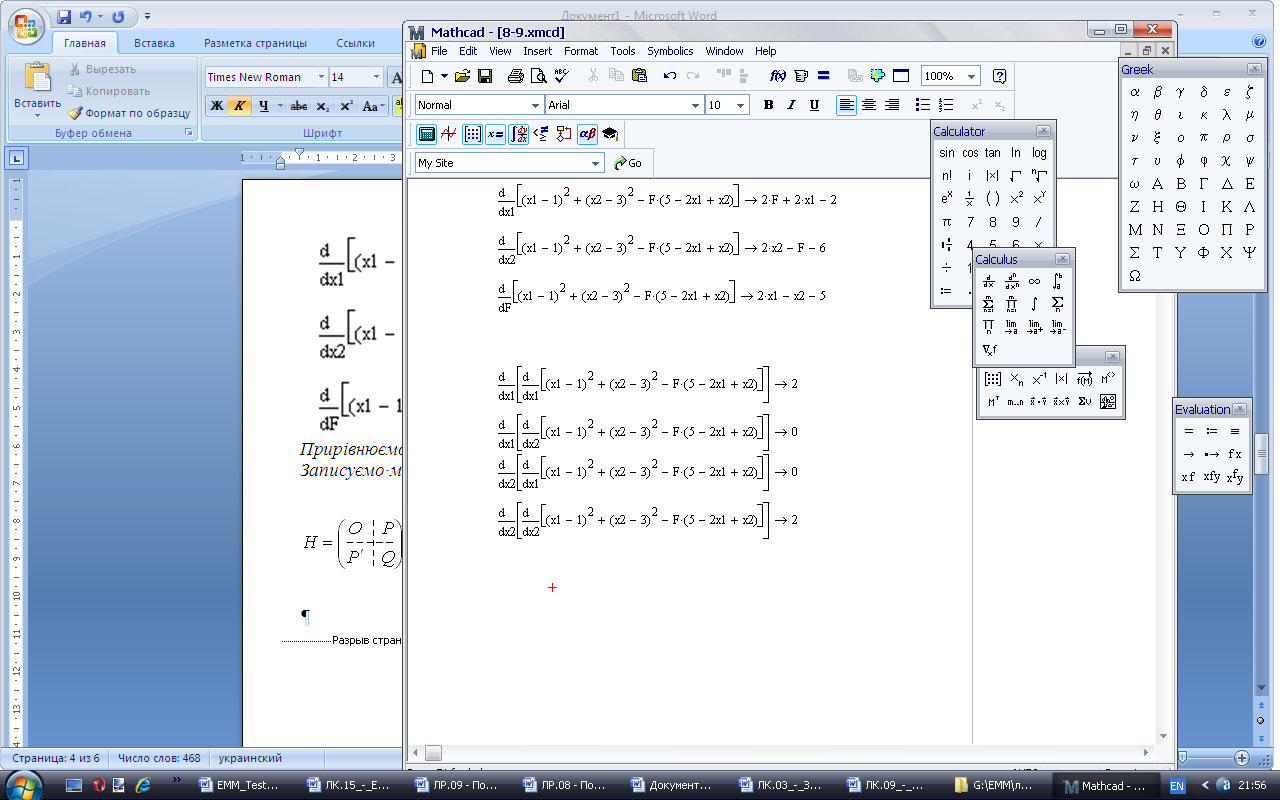
Н=

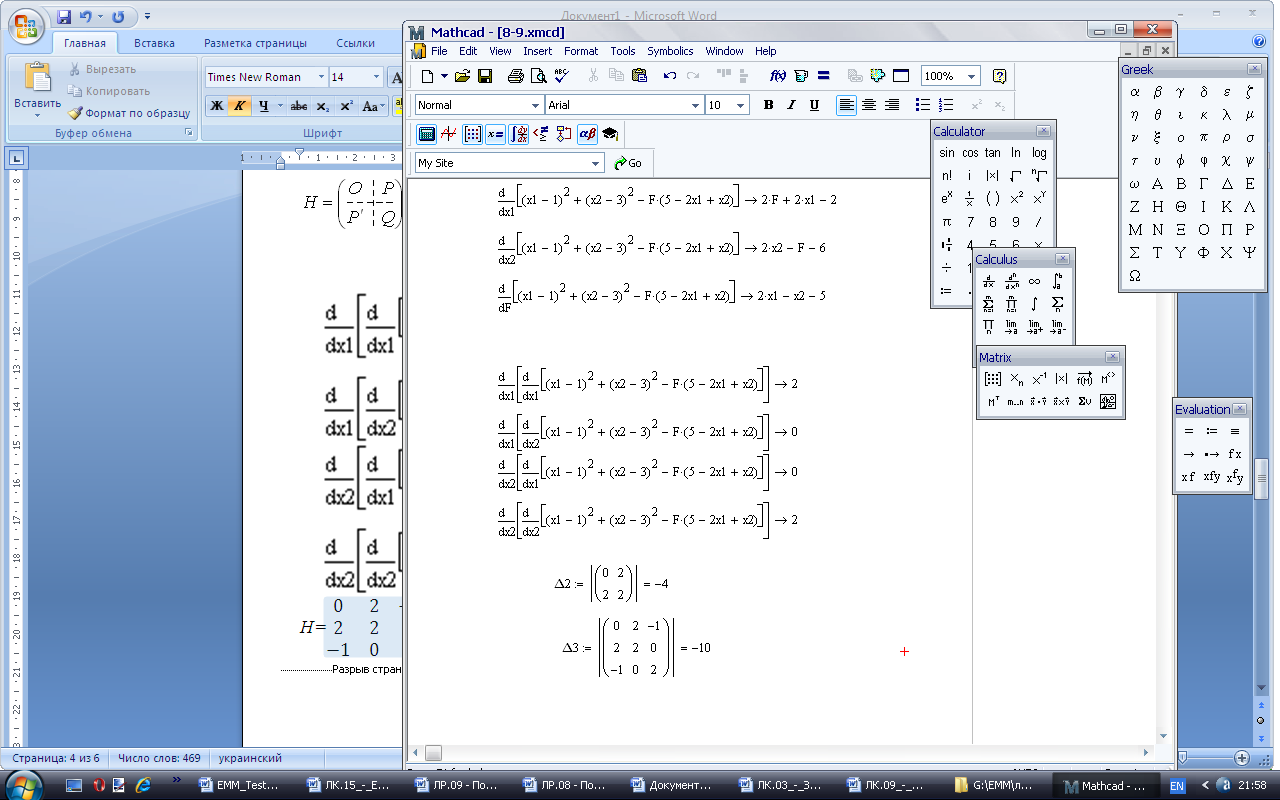
Це точка мінімуму

Білет №10.

№4. Запишемо двоїсту задачу до прямої задачі лінійного програмування:

max F = y₁ + 2 y₂;

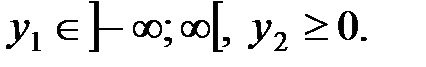
Перевіримо запропоновані плани на оптимальність.

1. Х = (8/7; 3/7; 0). Підставимо його в систему обмежень прямої задачі:

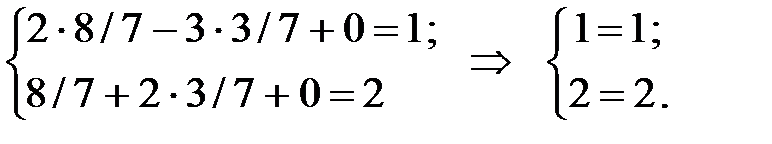
Х = (8/7; 3/7; 0) є допус­тимим планом

Z = 12 × 8/7 – 4 × 3/7 + 2 × 0 = 12.

Скористаємося другою теоремою двоїстості та визначимо відповідний план двоїстої задачі. Оскільки x₁ = 8/7 > 0; x₂ = 3/7 > 0, то згідно з другою частиною другої теореми двоїстості можна записати перше та друге обмеження як рівняння і визначити у₁ та у₂:

Підставимо ці значення в третє обмеження системи двоїстої задачі:

;

.

Для визначених значень у₁ = 4; у₂ = 4 це обмеження не виконується, і тому відповідний план у = (4; 4) є недопустимим планом двоїстої задачі. Отже Х = (8/7; 3/7; 0) виявився не оптимальним планом прямої задачі.

2. Х = (0; 1/5; 8/5). Підставимо цей план у систему обмежень прямої задачі:

План допустимий, і для нього Z = 12 × 0 – 4 × 1/5 + 2 × 8/5 = 12/5.

Оскільки компоненти x ₂ та x ₃ додатні, то друге і третє обмеження двоїстої задачі можна записати як рівняння:

Перевіримо, чи виконується перше обмеження двоїстої задачі для визначених значень у₁ та у₂: 2 × 8/5 + 2/5 = 18/5 < 12. Отже, перше обмеження виконується, і тому у = (8/5; 2/5) є допустимим планом двоїстої задачі. Для нього

F = 8/5 + 2 × 2/5 = 12/5 = Z.

З огляду на викладене можна зробити висновок, що Y* = (8/5; 2/5) є оптимальним планом двоїстої задачі, а X* = (0; 1/5; 8/5) – оптимальним планом прямої задачі.

3. Х = (1/3; 0; 1/3). Для цього плану обмеження прямої задачі виконуються так:

Оскільки Х = (1/3; 0; 1/3) є недопустимим планом, то він не може бути також оптимальним планом прямої задачі.

Отже, перевірка запропонованих планів на оптимальність дала такі результати:

а) ні;

б) так, Х* = (0; 1/5; 8/5), min Z = 12/5;

в) ні.

Білет № 11.

№4. Запишемо двоїсту задачу до прямої задачі лінійного програмування:

min F = 10 y₁ + 2 y₂;

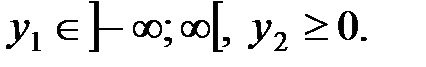
Перевіримо запропоновані плани на оптимальність.

1. Х = (0; 4; 2). Підставимо його в систему обмежень прямої задачі:

Х = (0; 4; 2) є допус­тимим планом

Z = 5 × 0 – 12 × 4 + 4 × 2 = -40.

Скористаємося другою теоремою двоїстості та визначимо відповідний план двоїстої задачі. Оскільки x2 = 4 > 0; x₃ = 2 > 0, то згідно з другою частиною другої теореми двоїстості можна записати третє та друге обмеження як рівняння і визначити у₁ та у₂:

Підставимо ці значення в перше обмеження системи двоїстої задачі:

;

.

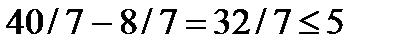Для визначених значень у₁ = 40/7; у₂ = -4/7 це обмеження не виконується, і тому відповідний план у = (40/7; -4/7) є недопустимим планом двоїстої задачі.

2. Х = (14/5;18/5;0). Підставимо цей план у систему обмежень прямої задачі:

План допустимий, і для нього Z = 5 × 14/5 + 12 × 18/5 + 4 × 0 = 286/5.

Оскільки компоненти x1 та x2 додатні, то друге і перше обмеження двоїстої задачі можна записати як рівняння:

Перевіримо, чи виконується третє обмеження двоїстої задачі для визначених значень у₁ та у₂ 29/5 -6/5 = 23/5 > 4. Отже, третє обмеження виконується, і тому у = (19/3; -2/3) є допустимим планом двоїстої задачі. Для нього:

F = 10*29/5 + 2 × -2/5 = 286/5 = Z.

З огляду на викладене можна зробити висновок, що Y* = (29/5; -2/5) є оптимальним планом двоїстої задачі, а X* = (14/5;18/5;0) – оптимальним планом прямої задачі.

3Х = (5/3;7/3;1/3). Підставимо цей план у систему обмежень прямої задачі:

План допустимий, і для нього Z = 5 × 5/3 – 12 × 7/3 + 4 × 1/3 = 55/3.

Оскільки всі компоненти додатні, то обмеження двоїстої задачі можна записати як рівняння:

і тому Х = (5/3;7/3;1/3) є неоптимальним планом прямої задачі.

Отже, перевірка запропонованих планів на оптимальність дала такі результати:

а) ні; б) так, Х* = (14/5;18/5;0), min Z = 12/5; в) ні.

БИЛЕТ №12

Гомори

Баз.	Сб.	Ао	-4
А1	А2	А3	А4	А5
Х1	-4	7\2		-5\2		5\2	-3\2
Х3		5\2		1\2		31\2	11\2
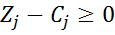
	-9

Для 2-го рядка дод. Обмеження:

Баз.	Сб	Ао	-4						-М
А1	А2	А3	А4	А5	А6	А7
А1	-4	7/2		-5/2		5/2	-3/2			-
А3		5/2		1/2		31/2	11/2
А7	-М	1/2		1/2		1/2	1/2	-1
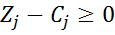
	-9-1/2M		10-1/2M		21-1/2M	14-1/2M	M

Баз.	Сб	Ао	-4						-М
А1	А2	А3	А4	А5	А6	А7
А1	-4							-5
А3									-1
А2								-2
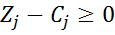
	-19							-20+M

=(6;1;2;0;0)

Білет №13

4 ) На основі умовно-оптимального плану цілочисельної задачі побудувати допоміжне обмеження Гоморі, приєднати його до умовно-оптимального плану, показаного у наведений нижче таблиці, і знайти цілі значення змінних задачі лінійного програмування.

Базис	Сб	А0		-1
А1	А2	А3	А4	А5
Х1		14/3		-2/3		5/3	1/3
Х3		11/3		1/3		7/3
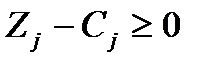
	47/3		4/3		14/3	11/3

Розв’язання

{0}*x1+{1/3}*x2+{1}*x3+{7/3}*x4+{1}*x5>={11/3}

1/3*x2+1/3*x4>=2/3

1/3*x2+1/3*x4-x6+xф=2/3

Базис	Сб	А0		-1					-M
x1		14/3		-2/3		5/3	1/3
x3		11/3		1/3		7/3
xф	-M	2/3		1/3		1/3		-1
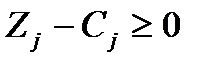
	-2/3*M+47/3		-1/3*M+4/3		-1/3*M+4/3	4/3	-M

Базис	Сб	А0		-1					-M
x1						7/3	1/3	-2
x3									-1
x2	-1							-3
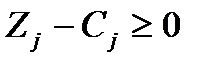
					10/3	4/3		M-4

Відповідь Х:(х1=6,х2=2,х3=3)

завдання 5.

Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

, .

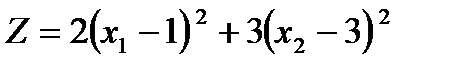Розв'язок.

Для того, щоб визначити точку та характер умовного екстремуму, спочатку запишемо функцію Лагранжа для даної функції

,

Тепер знайдемо частинні похідні і прирівняємо їх до нуля

Вирішуючи дану систему знаходимо значення х₁ та х₂. Отримали точку 1,6;3,4).Тепер потрібно сформувати матрицю Гессе, що має блочну структуру розмірністю :

де О – матриця розмірністю 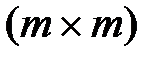, що складається з нульових елементів,

Р – матриця розмірністю 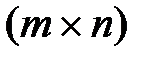, елементи якої визначаються так:

,

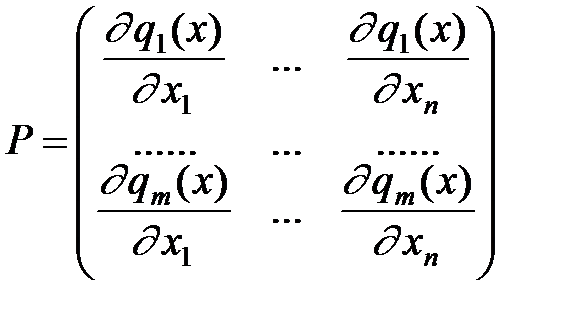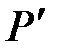– транспонована матриця до Р розмірністю ,

Q – матриця розмірністю виду:

, де .

Отже матриця Гессе має вигляд

Тепер визначаємо головні мінори

,

.

Отже, оскільки був отриманий не знакоперемінний ряд, робимо висновок, що отримана точка – це умовний мінімум функції.

Значення цільової функції у даній точці складає:

Билет 16.

1. Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:

Розв'язання. Необхідно пряму задачу звести до стандартного вигляду. Оскільки цільова функція Z максимізує і в системі обмежень є нерівності зі знаком «», то їх слід звести до виду «≤». Тому дані обмеження задачі помножимо на (–1). Після цього знак нерівності зміниться на протилежний.

.

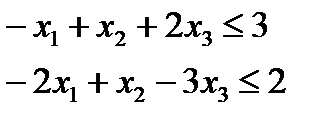За відповідними правилами побудуємо двоїсту задачу: mіп F = 3y₁ + 2y₂;

Задачі несиметричні. Двоїста задача має дві змінні, а отже, її можна розв’язати графічно.

Найменшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:

→

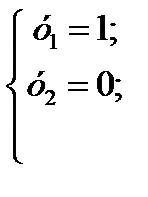
Отже, Y* = (1; 0); mіп F = 3 × 1+ 2*0 = 3.

Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.

Підставимо Y* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:

→

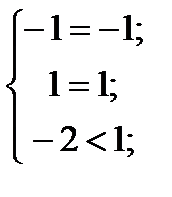
Оскільки останнє обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то висновуємо, що третя змінна прямої задачі дорівнюватиме нулю х₃ = 0 (перша частина другої теореми двоїстості).

Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки перші компоненти плану у₁ = 1 та у₂ = 0 додатні, то обидва обмеження прямої задачі для Х* виконуватиметься як строгі рівняння (друга частина другої теореми двоїстості).

Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х₃ = 0, та визначити решту змінних:

тобто Х* = (-1; 2; 0),

mах Z = -1 × (-1) + 1*2 + 1 × 0 = 3.

Умова min Z = max F = 3 виконується, і тому

Х* = (-1; 2; 0); Y* = (1;0)

є оптимальними планами відповідно прямої та двоїстої задач.

2. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

,

Вводимо в цільову функцію множник лагранжа:

Z(x1,x2,λ1, λ2)= 3x1²+2x2² + λ1(4-2x1-3x2) + λ2(8-x1-2x2)

Знаходимо похідні: По х1: 6х1-4 λ1- λ2; х2: 4х2-3λ1-2 λ2;

λ1: 4-2x1-3x2; λ2: 8-x1-2x2

Прирівнюємо похідні виражені через лямбда

Звідси: х1=-16; х2=12; λ1=-240; λ2=384

Формуємо матрицю Гессе:

0 0 2 3

= 0 0 1 2

2 1 6 0

3 2 0 4

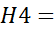Визначаємо мінори 3-го та 4-го порядку: =0 =13

Маємо знакосталий ряд, що визначає нашу функцію на мінімум.

Значення ЦФ=1056

Билет 17.

1.Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:

Розв'язання.За відповідними правилами побудуємо двоїсту задачу: mах F = y₁ + 3y₂;

Задачі несиметричні. Двоїста задача має дві змінні, а отже, її можна розв’язати графічно.

Найбільшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:

→

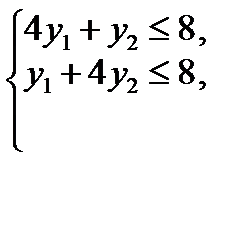
Отже, Y* = (1,6; 1,6); mах F = 1,6+ 3*1,6 = 6,4.

Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.

Підставимо Y* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:

→

Оскільки останнє обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то висновуємо, що третя змінна прямої задачі дорівнюватиме нулю х₃ = 0 (перша частина другої теореми двоїстості).

Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки перші компоненти плану у₁ = 1 та у₂ = 0 додатні, то обидва обмеження прямої задачі для Х* виконуватиметься як строгі рівняння (друга частина другої теореми двоїстості).

Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х₃ = 0, та визначити решту змінних:

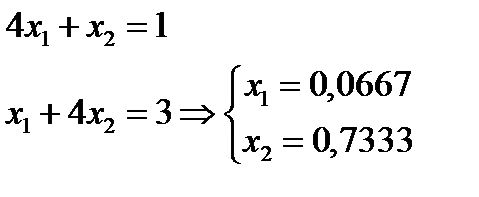
тобто Х* = (0,667; 0,7333; 0),

min Z = 8 × 0,667+ 8*0,7333 + 1 × 0 = 6,4.

Умова min Z = max F = 6,4 виконується, і тому

Х* = (0,667; 0,7333; 0); Y* = (1,6;1,6)

є оптимальними планами відповідно прямої та двоїстої задач.

2. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

,

Вводимо в цільову функцію множник лагранжа:

Z(x1,x2,λ1, λ2)= x2- x1-2x1² + λ1(12-3x1-4x2) + λ2(6+x1-2x2)

Знаходимо похідні:

По х1: -1-4х1-3 λ1+ λ2

х2: 1-4λ1-2 λ2

λ1:12-3x1-4x2

λ2: 6+x1-2x2

Прирівнюємо похідні виражені через лямбда

Звідси: х1=0; х2=3; λ1=-0.1; λ2=0.7

Формуємо матрицю Гессе:

0 0 3 4

= 0 0 -1 2

3 -1 -4 0

4 2 0 0

Визначаємо мінори 3-го та 4-го порядку:

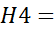=0; =100

Маємо знакосталий ряд, що визначає нашу функцію на мінімум.

Значення ЦФ=3.

Билет 18.

1. Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:

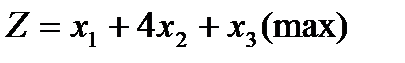
Розв'язання.За відповідними правилами побудуємо двоїсту задачу: mіп F = 2y₁ + 0y₂;

Задачі несиметричні. Двоїста задача має дві змінні, а отже, її можна розв’язати графічно.

Найменшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:

→

Отже, Y* = (-1,5; 7); mіп F = 2*(-1,5)+ 0*7 = -3.

Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.

Підставимо Y* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:

→

2 .Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

, .

Вводимо в цільову функцію множник лагранжа:

Z(x1,x2,λ1, λ2)= 8x1+2x1²+4x1х2+x2²+ λ1(6-6x1-2x2) + λ2(16-x1-8x2)

Знаходимо похідні: По х1: 8+4х1+4х2-6 λ1- λ2;

х2: 2х2+4х1-2 λ1-8 λ2; λ1: 6-6x1-2x; λ2: 16-x1-8x2

Прирівнюємо похідні виражені через лямбда

Звідси: х1=0.34; х2=1.96; λ1=-2.2112; λ2=1.213

Формуємо матрицю Гессе:

0 0 6 2

= 0 0 1 8

6 1 4 4

2 8 4 2

Визначаємо мінори 3-го та 4-го порядку:

=0

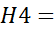=2116 Маємо знакосталий ряд, що визначає нашу функцію на мінімум.Значення ЦФ=9.57

БИЛЕТ №19

Дата добавления: 2015-10-31