
Читайте также:
|
БИЛЕТ №1
4) Побудуємо математичну модель:
Цільова ф-ція: Ф(х1,х2) = 300х1+400х2, прямує до максимуму
Обмеження: 15х1+40х2<=600
50х1+30х2<=900
х1+х2<=20
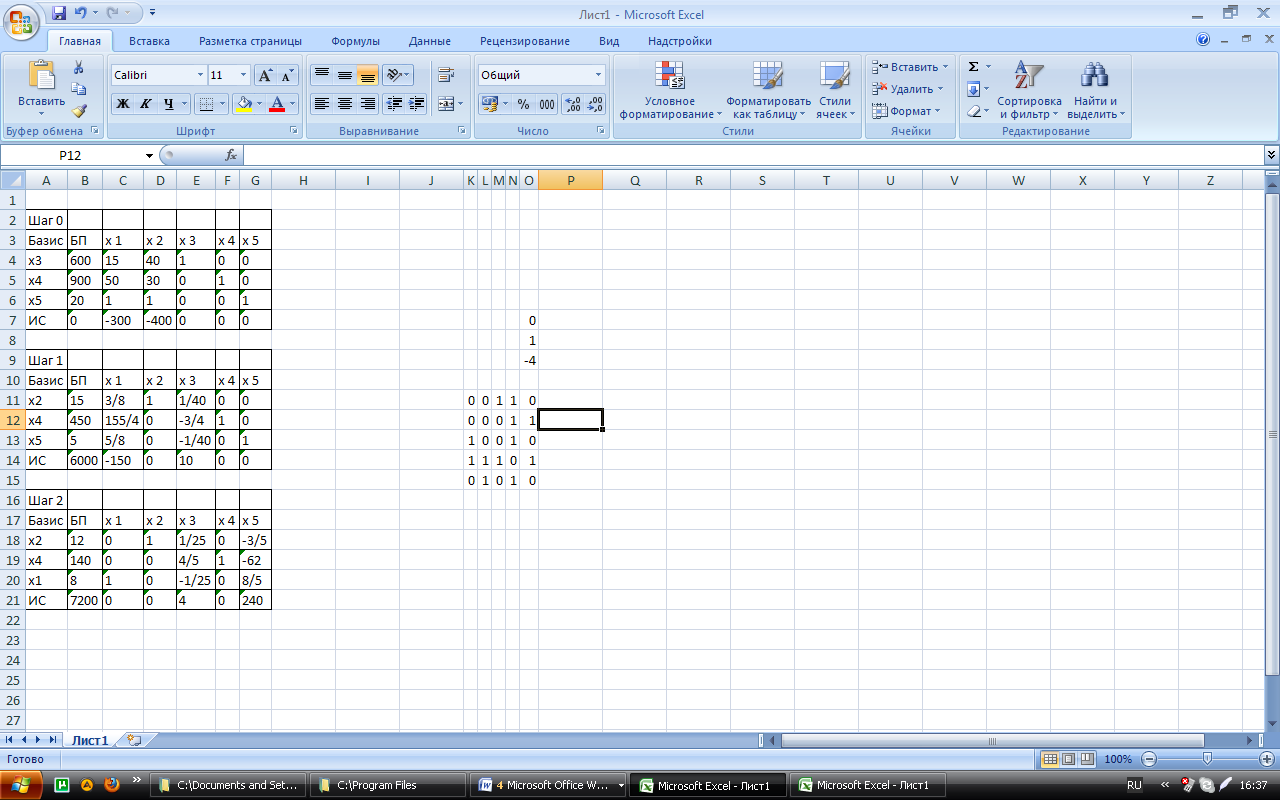
Розв‘яжемо задачу симплекс методом: Початкова симплекс таблиця
| Шаг 0 | ||||||
| Базис | БП | x 1 | x 2 | x 3 | x 4 | x 5 |
| x3 | ||||||
| x4 | ||||||
| x5 | ||||||
| ИС | -300 | -400 |
| Шаг 1 | ||||||
| Базис | БП | x 1 | x 2 | x 3 | x 4 | x 5 |
| x2 | 3/8 | 1/40 | ||||
| x4 | 155/4 | -3/4 | ||||
| x5 | 5/8 | -1/40 | ||||
| ИС | -150 |
| Шаг 2 | ||||||
| Базис | БП | x 1 | x 2 | x 3 | x 4 | x 5 |
| x2 | 1/25 | -3/5 | ||||
| x4 | 4/5 | -62 | ||||
| x1 | -1/25 | 8/5 | ||||
| ИС |
Оптимальний план x = (8, 12) Ф(x)= 7200
Будуємо двоїсту задачу Ф(у) = 600у1+900у2+20у3 прямує до min Обмеження:15у1+50у2+у3>=300; 40у1+30у2+у3>=400
Розв‘яжемо задачу симплекс методом
| Шаг 0 | ||||||||
| Базис | БП | y 1 | y 2 | y 3 | y 4 | y 5 | z 1 | z 2 |
| z1 | -1 | |||||||
| z2 | -1 | |||||||
| ИС | -700M | -55M+600 | -80M+900 | -2M+20 | M | M |
Елемент (1,2)
| Баз | БП | y 1 | y 2 | y 3 | y 4 | y 5 | z 1 | z 2 |
| y2 | 3/10 | 1/50 | -1/50 | 1/50 | ||||
| z2 | 2/5 | 3/5 | -1 | -3/5 | ||||
| ИС | -220M-5400 | -31M+330 | -2/5M+2 | -3/5M+18 | M | 8/5M-18 |
Елемент(2,1)
| Базис | БП | y 1 | y 2 | y 3 | y 4 | y 5 | z 1 | z 2 |
| y2 | 120/31 | 1/62 | -4/155 | 3/310 | 4/155 | -3/310 | ||
| y1 | 220/31 | 2/155 | 3/155 | -1/31 | -3/155 | 1/31 | ||
| ИС | -240000/31 | -70/31 | 360/31 | 330/31 | M-360/31 | M-330/31 |
Елемент(1,3)
| Базис | БП | y 1 | y 2 | y 3 | y 4 | y 5 | z 1 | z 2 |
| y3 | -8/5 | 3/5 | 8/5 | -3/5 | ||||
| y1 | -4/5 | 1/25 | -1/25 | -1/25 | 1/25 | |||
| ИС | -7200 | M-8 | M-12 |
Розв‘язок y* = (4, 0, 240) f(x*)= 7200
Двоїста оцінка для ресурсу шліфувального апарату – у1 = 4, тобто при збільшенні ресурсу на 1, цільова ф-ція зросте на 4.
5 ) L(x1,x2,x3,λ1,λ2) = x1x2+x2x3+λ1(x1+x2-4)+λ2(x2+x3-4)
Отримали систему рівнянь: х2+λ1 = 0; х1+х3+λ1+λ2 = 0; х2+λ2 = 0; х1+х2-4 = 0; х2+х3 – 4 = 0
Розв‘яжемо її: х2=-λ1; λ1=λ2; х1=4-х2; х3=4-х2; х1=х3
4-х2+4-х2-х2-х2=0; х2=2; λ1=λ2=-2є; х1=2; х3=2
Побудуємо матрицю Гессе
Визначники мінорів створюють знакозмінний ряд (0,1,-4)
Точка (2,2,2) – точка максимуму
БИЛЕТ №2
4) Розглядаємо 1 квадрант (адже х1 та х2>0)
Нанесемо обмеження на координатну площину, обмежена область зоображена зафарбованою червоним кольором
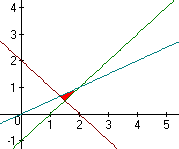
Опускаємо цільову ф-цію (вектор руху перпендикулярний прямій У(х)=х/2) так, щоб вона ще перетиналася з областю, яку визначили наші обмеження, вона буде перетинатися в точці, створеній перетинами 2 прямих:
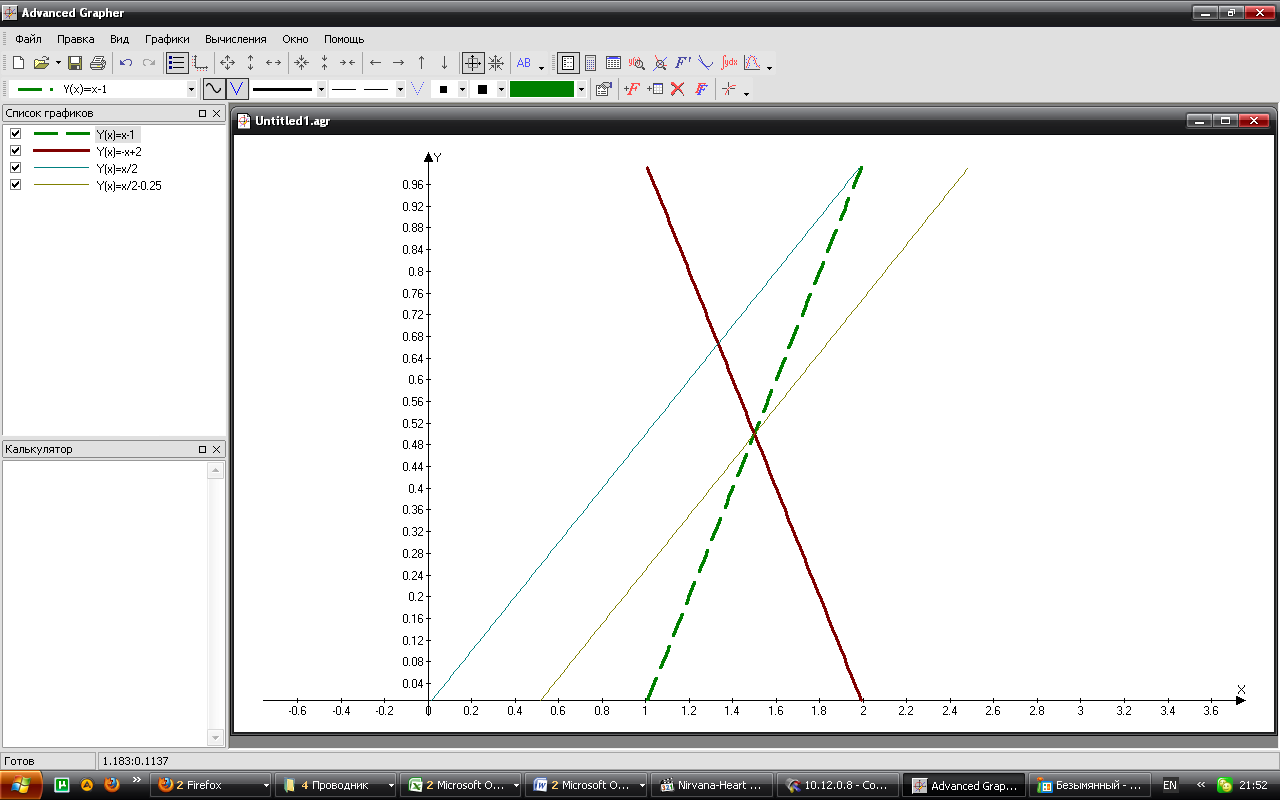
х-1=-х+2; 2х=3
Розв‘язком є точка з координатами
х1=1,5; х2=0,5 значення цільової ф-ції в цій точці 0,5.
5) Z=-2x1^2+3x2^2+4x1+5
Похідна по х1: -4х1+4
по х2:6х2
Прирівнюємо до 0, отримуємо систему
-4х1+4=0, х1=1,
6х2=0; звідси х2=0;
Перевіримо отриману точку.
Нехай A = Zxx(x1,x2); B = Zxy(x1,x2); C = Zyy(x1,x2); D = AC – B^2.
A=-4, B=0, C=6, D=-24. Оскільки D<0, то знайдена точка не э точкою екстремуму. Отже ф-ція не має екстремумів.
БИЛЕТ № 4
4) Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис.1.1.).
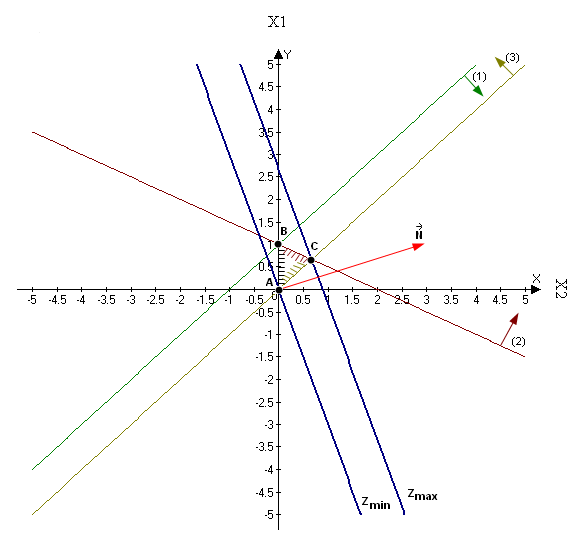
Побудуємо вектор 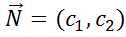 ,
, 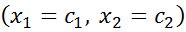 .
. 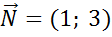 .
.
Із рис.1.1 видно, що крайніми спільними точками прямої цільової функції та трикутника ABC є точки A та С. Координати даних точок є оптимальними планами задачі.
Координати точки A є розв’язком системи рівнянь:
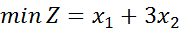 (1.1)
(1.1)
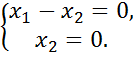 (1.2)
(1.2)
звідси маємо: 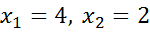 .
.
Отже, 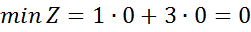
Координати точки С є розв’язком системи рівнянь:
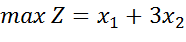 (1.1)
(1.1)
 (1.2)
(1.2)
звідси маємо: 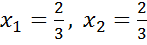 . Отже,
. Отже, 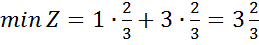
2) 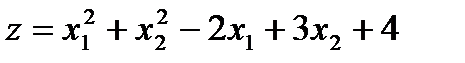
Знайдемо перші похідні та прирівняємо їх до нуля:

Розв’язавши систему, маємо:

Для того, щоб перевірити чи є дана точка екстремумом та визначити тип екстремуму використаємо перевірку достатньої умови:

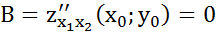
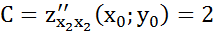
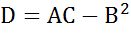
Тоді, якщо D < 0, то в точці (x0,y0) екстремума немає. Якщо D > 0, то в точці (x0,y0) екстремум функції z, причому якщо A > 0, то мінімум, а якщо A < 0, то максимум. Якщо D = 0, то екстремум може бути, а може і не бути. В даному випадку потрібні додаткові дослідження.
В нашому випадку

Отже маємо точку мінімуму.
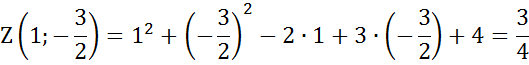
БИЛЕТ №5
4) Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис.1.1.).

Побудуємо вектор 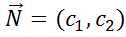 ,
, 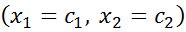 .
. 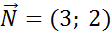 .
.
Із рис.1.1 видно, що ОДЗ є не замкнутою і ЦФ має лише один екстремум (min).
Координати точки B є розв’язком системи рівнянь:
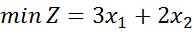 (1.1)
(1.1)
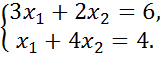 (1.2)
(1.2)
звідси маємо: 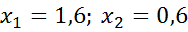 .
.
Отже, 
5) Визначити точку та характер умовного екстремуму функції за методом множників Лагранжа.
 ,
,
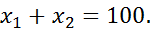 (5.1)
(5.1)
Розв’язання
Маємо задачу лінійного програмування:
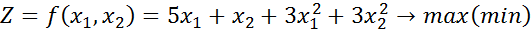 (5.2)
(5.2)
при обмеженні
 (5.3)
(5.3)
Для знаходження розв’язку даної задачі спочатку слід замінити нашу цільову функцію більш складнішою – функцією Лагранжа.
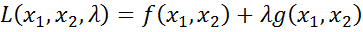 (5.4)
(5.4)
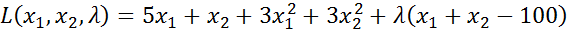 (5.5)
(5.5)
де 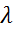 – множник Лагранжа.
– множник Лагранжа.
Визначимо частинні похідні 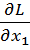 ,
,  ,
,  побудованої функції Лагранжа:
побудованої функції Лагранжа:
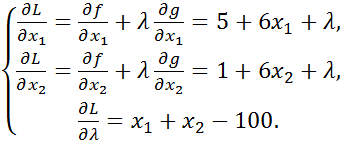 (5.6)
(5.6)
Далі прирівняємо знайдені частинні похідні до нуля:
 (5.7)
(5.7)
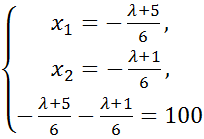 (5.8)
(5.8)
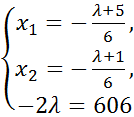 (5.8)
(5.8)
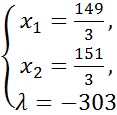 (5.8)
(5.8)
Наступним кроком є побудова матриці Гессе, що має блочну структуру розмірністю 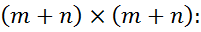
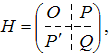
(5.9)
де О – матриця розмірністю 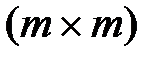 , що складається з нульових елементів;
, що складається з нульових елементів;
Р – матриця розмірністю 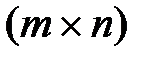 , елементи якої визначаються наступним чином:
, елементи якої визначаються наступним чином:
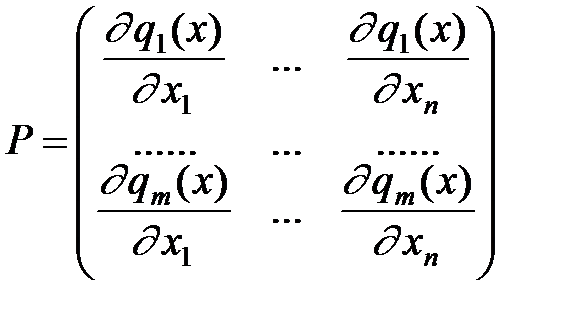 , (5.10)
, (5.10)
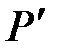 – транспонована матриця до Р розмірністю
– транспонована матриця до Р розмірністю  ,
,
Q – матриця розмірністю  виду:
виду:
 , де
, де  . (5.11)
. (5.11)
У нашому випадку матриця Гессе матиме наступний вигляд:
 (5.19)
(5.19)
Визначаємо головні мінори матриці Гессе, починаючи з 2-го порядку:
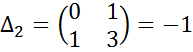 (5.19)
(5.19)
 (5.20)
(5.20)
Як бачимо, головні мінори утворюють знакоcталий ряд, тобто наша точка 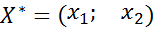 є точкою мінімуму.
є точкою мінімуму.
Обчислимо значення цільової функції у знайденій точці:
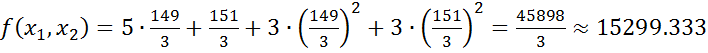
БИЛЕТ № 6
4) Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис.1.1.).
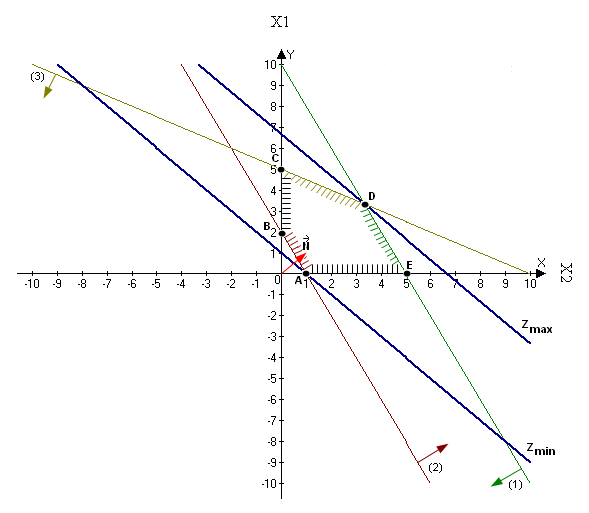
Побудуємо вектор 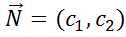 ,
, 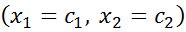 .
.  .
.
Із рис.1.1 видно, що крайніми спільними точками прямої ЦФ та 5-кут ABCDE є точки A та D. Координати точок є опт планами задачі.
Координати точки A є розв’язком системи рівнянь:
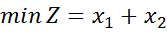 (1.1)
(1.1)
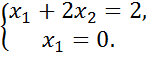 (1.2)
(1.2)
звідси маємо: 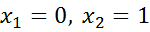 .
.
Отже, 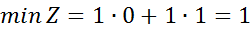
Координати точки D є розв’язком системи рівнянь:
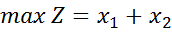 (1.1)
(1.1)
 (1.2)
(1.2)
звідси маємо: 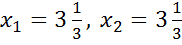 .
.
Отже, 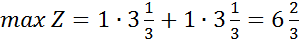
5 ) Визначити точку та характер умовного екстремуму функції за методом множників Лагранжа.
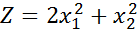 ,
,
 (5.1)
(5.1)
Розв’язання
Маємо задачу лінійного програмування:
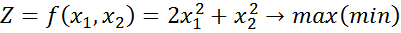 (5.2)
(5.2)
при обмеженні
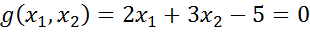 (5.3)
(5.3)
Для знаходження розв’язку даної задачі спочатку слід замінити нашу цільову функцію більш складнішою – функцією Лагранжа.
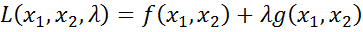 (5.4)
(5.4)
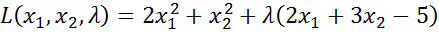 (5.5)
(5.5)
де 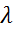 – множник Лагранжа.
– множник Лагранжа.
Визначимо частинні похідні 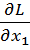 ,
,  ,
,  побудованої функції Лагранжа:
побудованої функції Лагранжа:
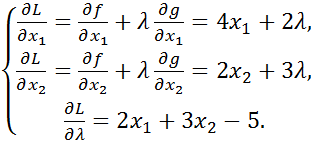 (5.6)
(5.6)
Далі прирівняємо знайдені частинні похідні до нуля:
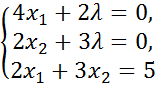
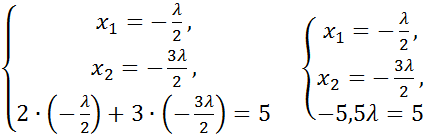
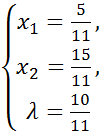 (5.8)
(5.8)
Наступним кроком є побудова матриці Гессе, що має блочну структуру розмірністю 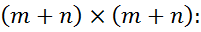
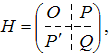
(5.9)
де О – матриця ро 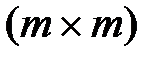 , скл. з нульових ел.
, скл. з нульових ел.
Р – матриця 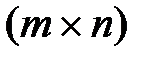 , елементи якої визн. наступним чином:
, елементи якої визн. наступним чином:
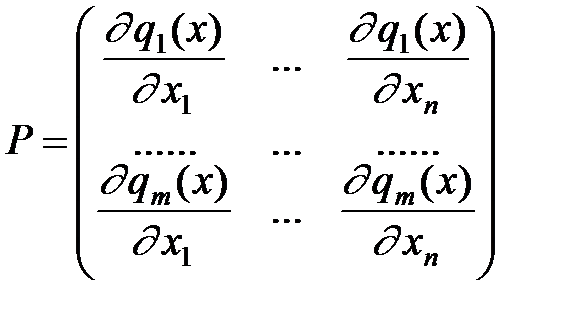 , (5.10)
, (5.10)
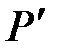 – транспонована матриця до Р розмірністю
– транспонована матриця до Р розмірністю  ,
,
Q – матриця розмірністю  виду:
виду:
 , де
, де  . 5.11)
. 5.11)
У нашому випадку матриця Гессе матиме наступний вигляд:
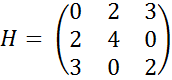 (5.19)
(5.19)
Визн. головні мінори матриці Гессе, починаючи з 2-го порядку:
 (5.19)
(5.19)
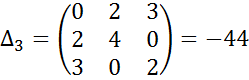 (5.20)
(5.20)
Як бачимо, головні мінори утворюють знакоcталий ряд, тобто наша точка 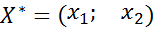 є точкою мінімуму.
є точкою мінімуму.
Обчислимо значення цільової функції у знайденій точці:
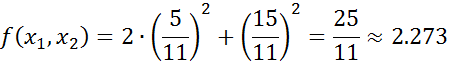
Білет №7
1. Розв’язати задачу лінійного програмування графічним методом: Z = 2x1 + 4x2 (max)
3x1 + 2x2 £ 11,
-2x1 + x2 £ 2,
-x1 + 3x2 ³ 0,
x1³ 0; x2 ³ 0.
1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі знаків нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3. Знаходимо багатокутник розв’язків задачі лінійного програмування.
4. Будуємо вектор 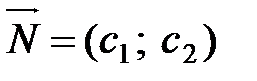 , що задає напрям зростання значення цільової функції задачі.
, що задає напрям зростання значення цільової функції задачі.
5. Будуємо пряму с1х1+с2х2=const, перпендикулярну до вектора  .
.
6. Рухаючи пряму с1х1+с2х2=const в напрямку вектора
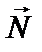 (для задачі максимізації) або в протилежному напрямі
(для задачі максимізації) або в протилежному напрямі
(для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального значення.
7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
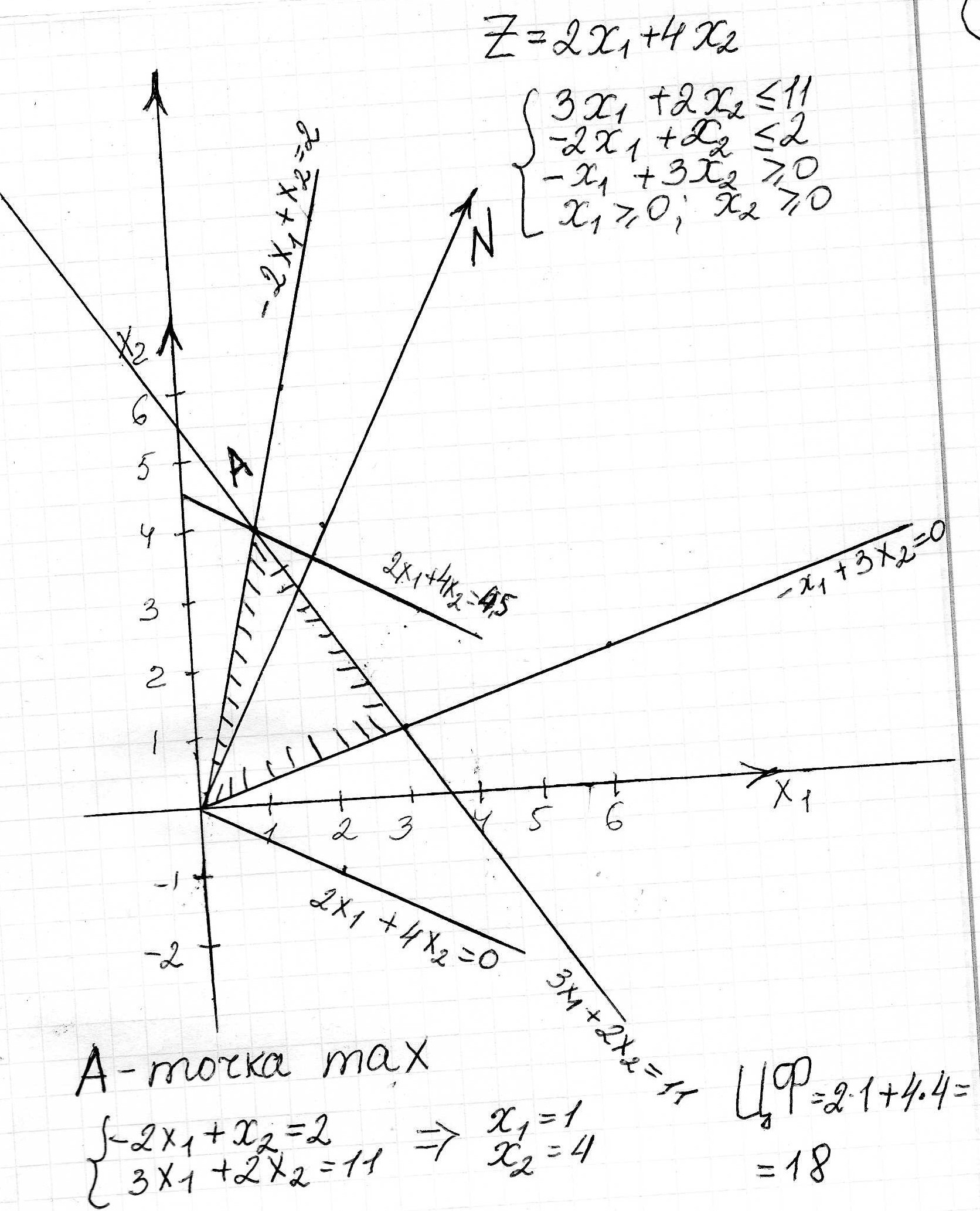
2. Викор. метод множн. Лагранжа, знайти т. умовн. Екстремуму ЗНП, визначити характер екстремуму:
 ,
, 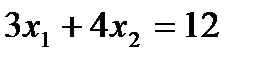 .
.

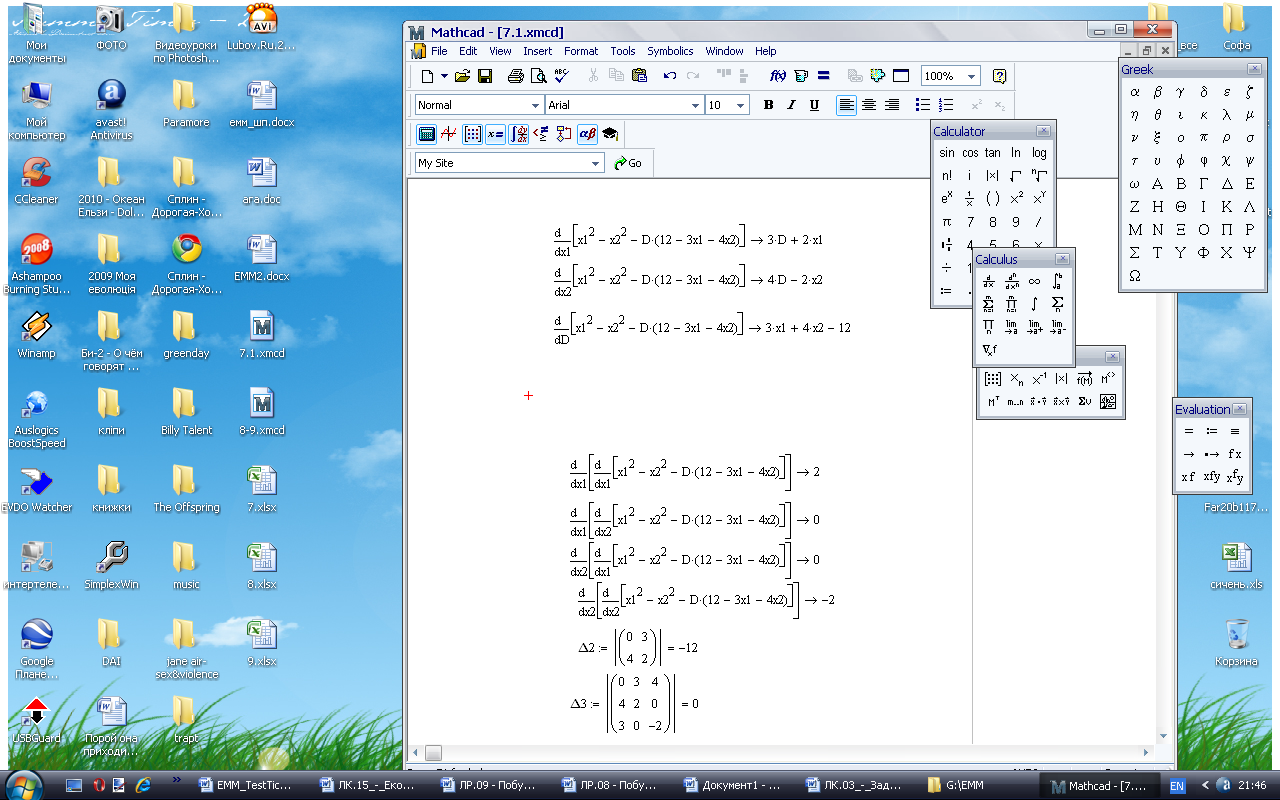
Прирівнюємо до нуля, розв’язуємо систему, з неї отримуємо х1=-5,13; х2=6,85; 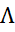 =3,42 Записуємо матрицю Гессе
=3,42 Записуємо матрицю Гессе

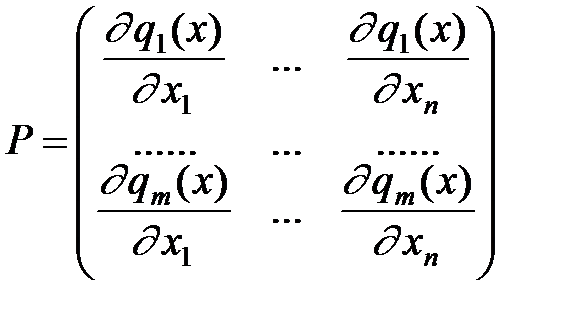

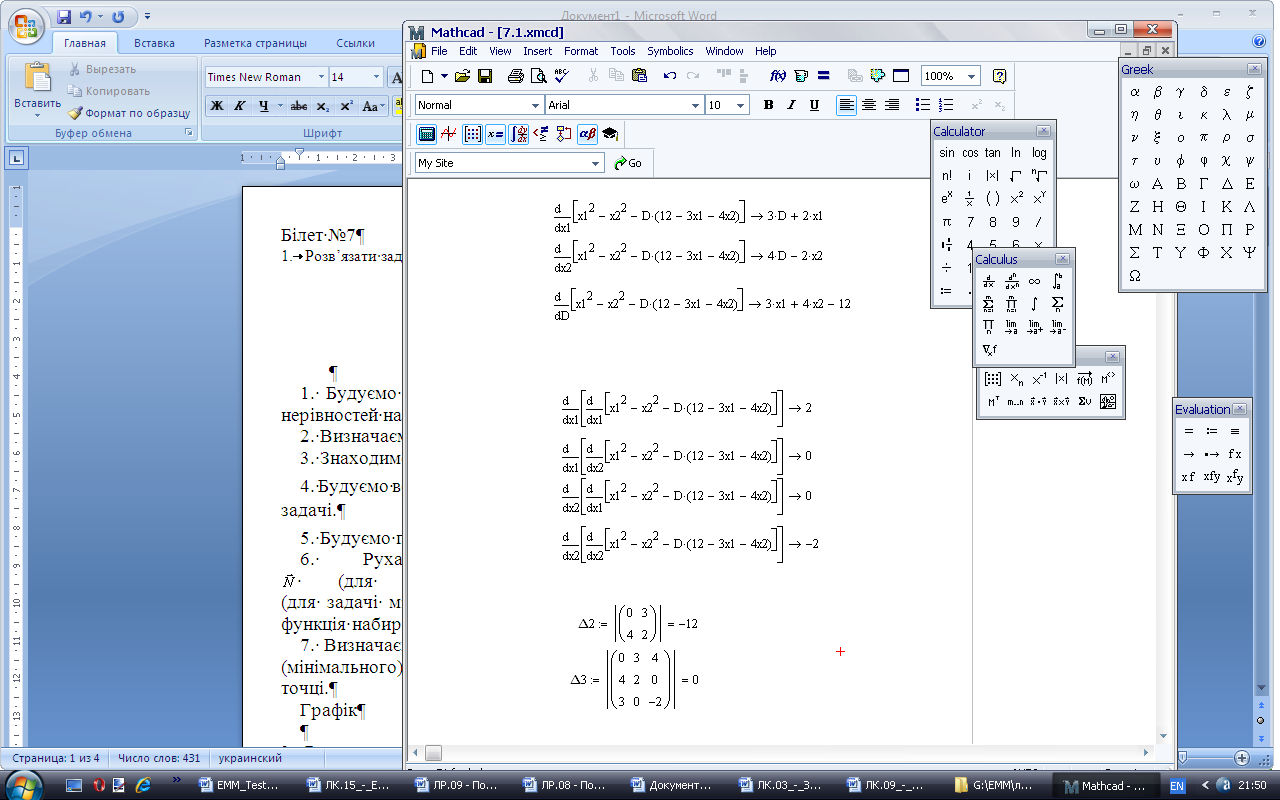
H= 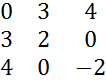 Знаходимо визначники
Знаходимо визначники 
Білет №8
1. Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
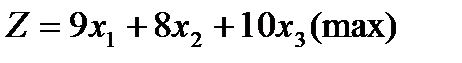
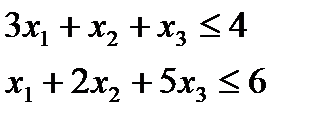
|
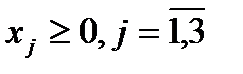
Двоїста задача
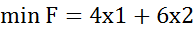
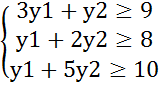
Графік

Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.
Підставимо знач точки А у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:
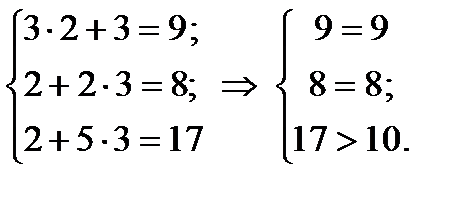
третє обмеження для опт плану двоїстої задачі виконується як строга нерівність, доходимо висновку, що третя змінна прямої задачі дорівнюватиме нулю х3 = 0 (перша частина другої теореми двоїстості).
Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки компоненти плану додатні,то обмеження прямої задачі для X * виконуватимуться як строгі рівняння (друга частина другої теореми двоїстості).
Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х3 = 0, та визначити решту змінних:
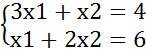 x1=2/5 x2=14/5 x3=0 ЦФ = 26
x1=2/5 x2=14/5 x3=0 ЦФ = 26
2. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:
 ,
,  .
.
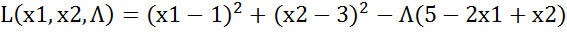
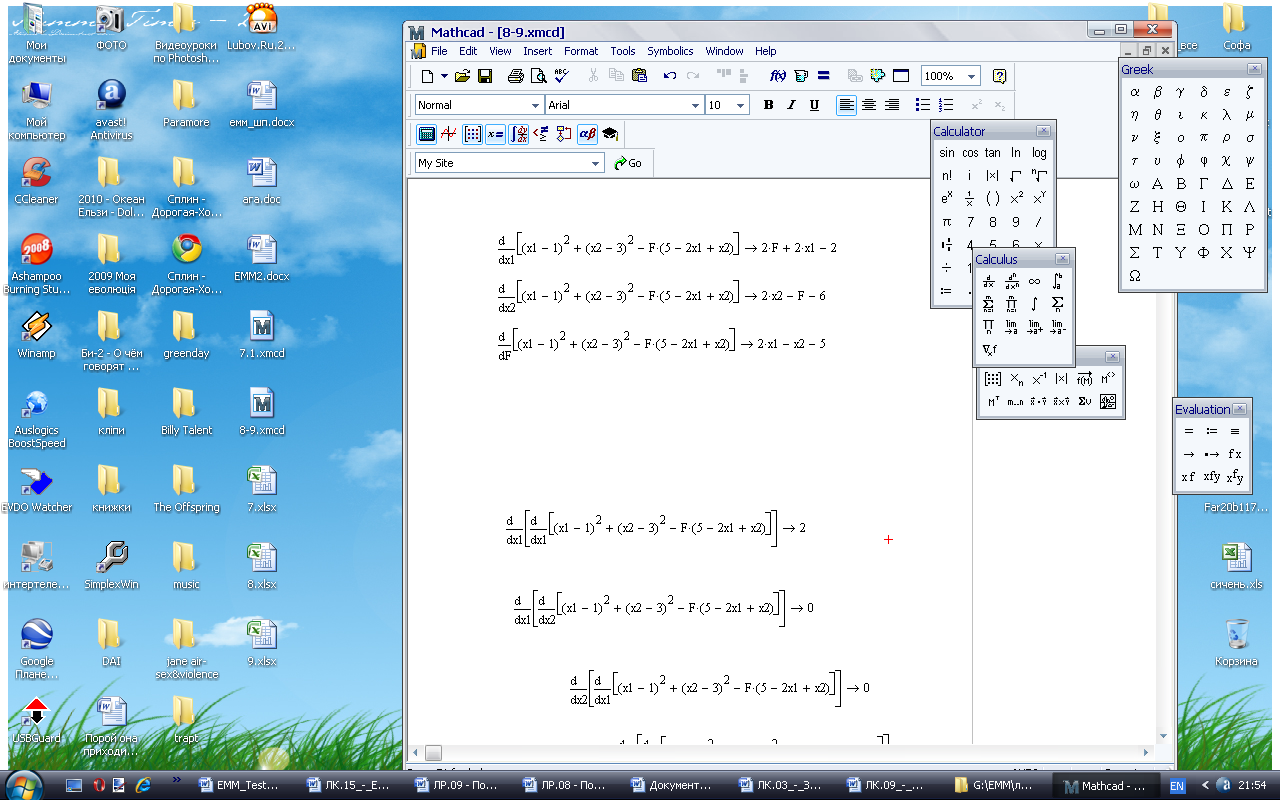
Прирівнюємо до нуля, розв’язуємо систему, з неї отримуємо х1=3,4; х2=1,8; 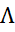 =-2,4
=-2,4
Записуємо матрицю Гессе

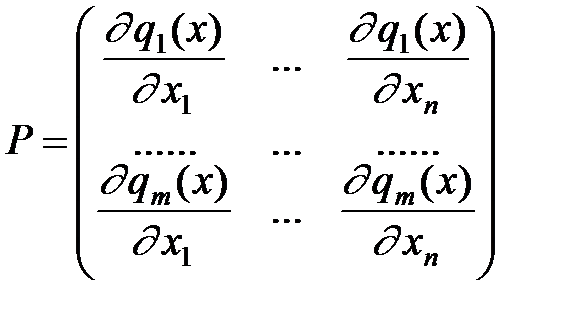

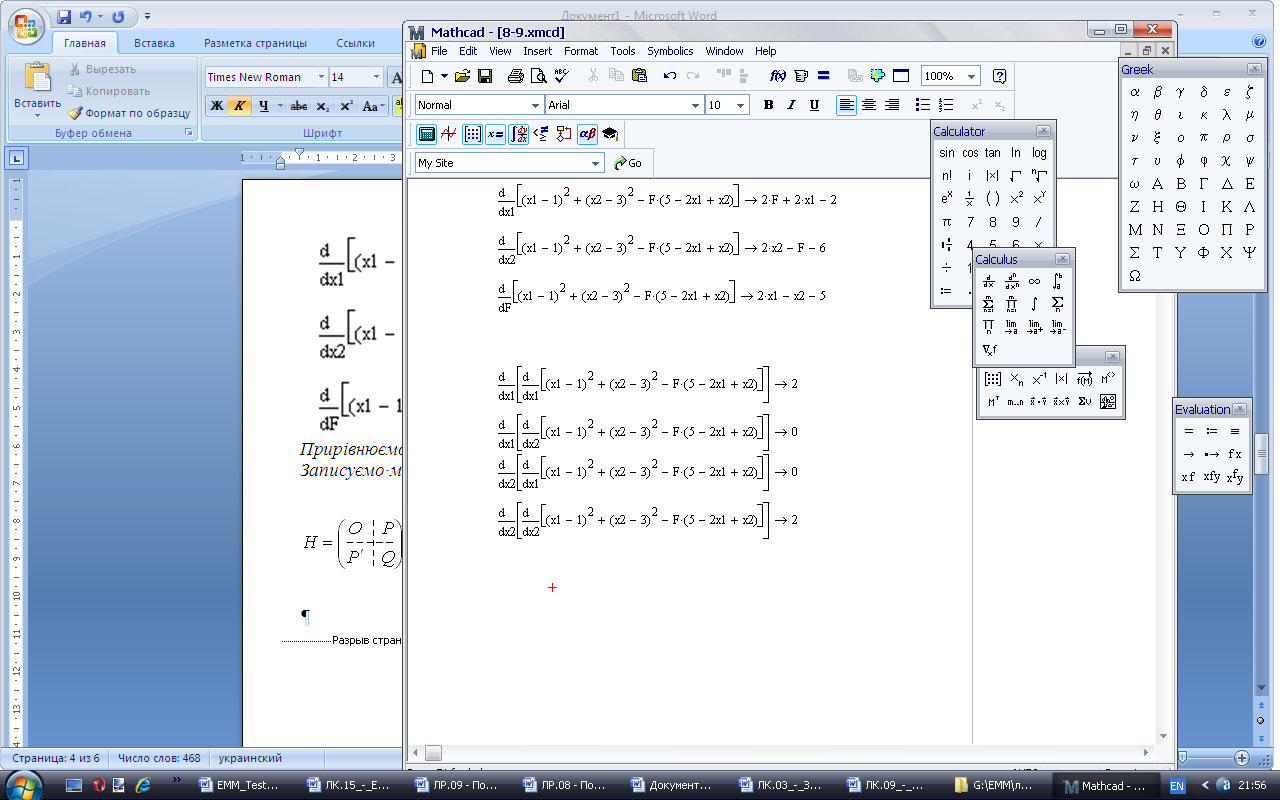
Н= 
Це точка мінімуму
Білет №9
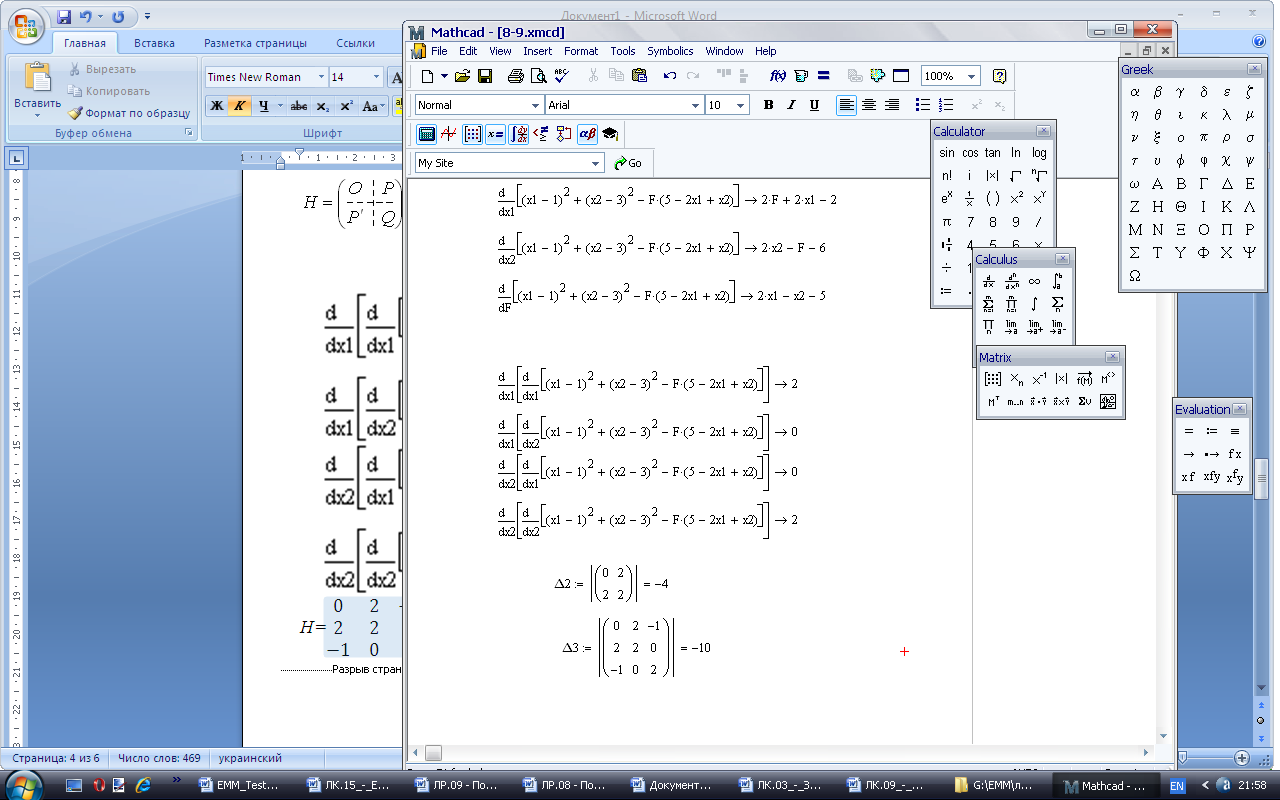
1. Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
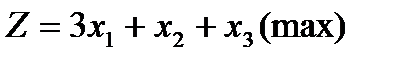
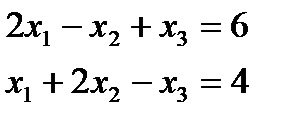
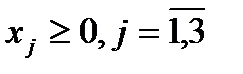
Двоїста задача


Графік
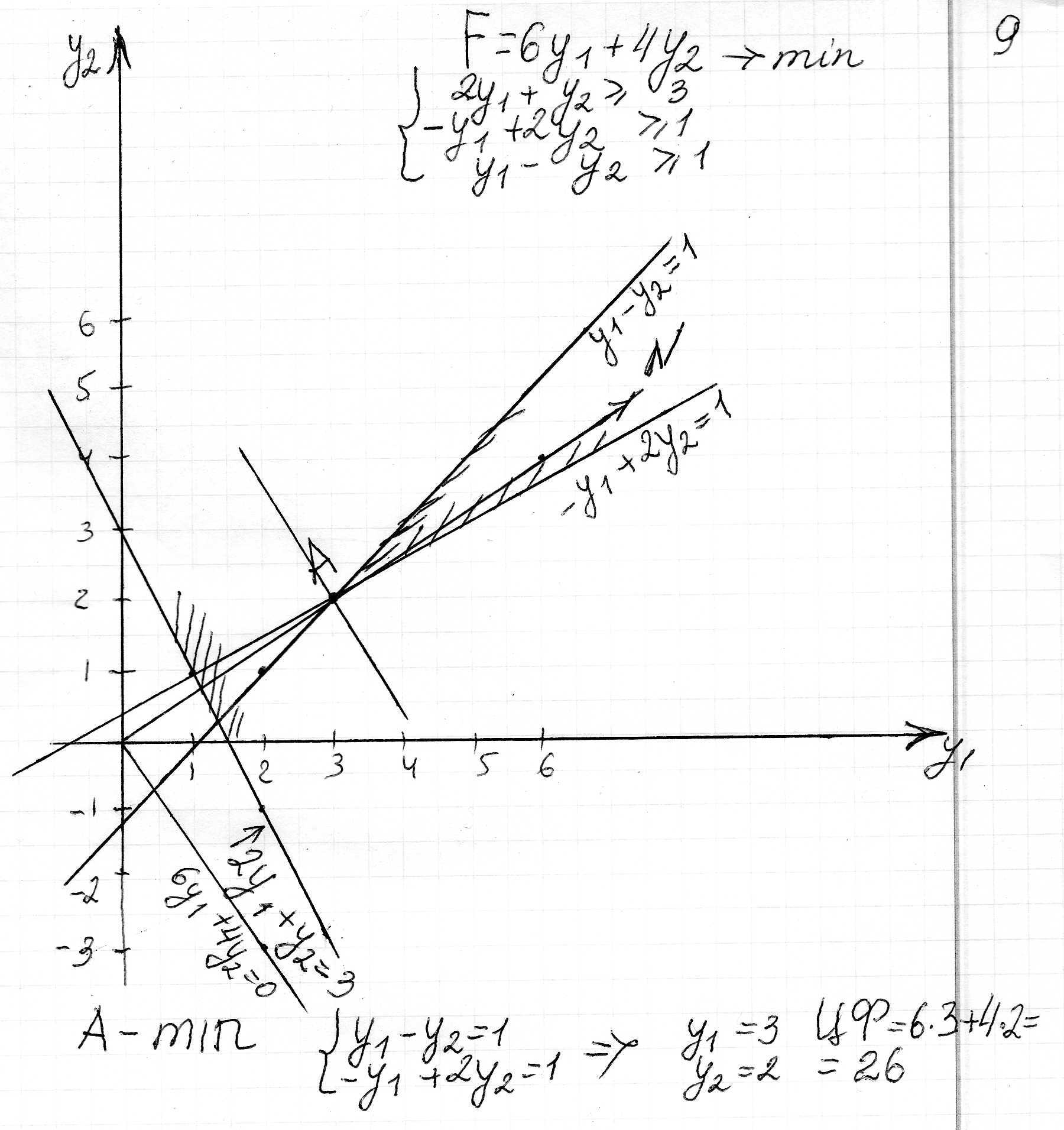
Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.
Підставимо знач точки А у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:
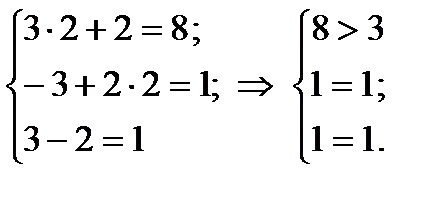
перше обмеження для опт плану двоїстої задачі виконується як строга нерівність, доходимо висновку, що перша змінна прямої задачі дорівнюватиме нулю х1 = 0 (перша частина другої теореми двоїстості).
Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки компоненти плану додатні,то обмеження прямої задачі для X * виконуватимуться як строгі рівняння (друга частина другої теореми двоїстості).
Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х1 = 0, та визначити решту змінних:
Дата добавления: 2015-10-31; просмотров: 151 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Практичне заняття № 19 | | | Екзамен.білет № 28 2 страница |