Екзамен.білет № 28 4 страница

По х1: 2х1-2- λ

х2: 2х2+3-2 λ

λ: 3-х1-2х2

Прирівнюємо похідні виражені через лямбда:

2х2+3=4х1-4 Звідси: х1=2; х2=0,5; λ=2

Формуємо матрицю Гессе:

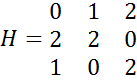
Визначаємо мінори 2-го та 3-го порядку:

=-2

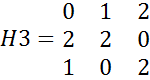=-8

Маємо знакосталий ряд, що визначає нашу функцію на мінімум.

Значення ЦФ=5,75

Білет№ 26

1. Розв’язати транспортну задачу:

ai = (5; 20; 10); bj = (10; 25;15);

.

де с_ij — вартість перевезення одиниці продукції від і -го постачальника до j -го споживача, а_i — запаси продукції і -го постачальника; b_j — попит на продукцію j -го спо­живача.

Перевіряємо нашу задачу на збалансованість. Оскільки сумарний попит перевищує запаси, вводимо фіктивний склад:

Формуємо опорний план за методом північно-західного кута.

Значення функції: Z = 5*3+5*6+8*15+10*2+15*10=335

За методом Степінг-Стоун перебираємо всі допустимі плани задачі, формуючи цикли та здійснюючи перебір пустих клітинок у кожному плані. Приклад:

5-	+
5+	15-

σ = 4-3+6-8=-1

Якщо значення сігма менше нуля, то існує кращий план і наявний можна поліпшити, за алгоритмом симплекс методу переходимо до нового плану. Процедуру повторюємо доти поки не знайдемо оптимальний план.

У даному випадку на 2-му етапі знаходимо оптимальний план:

Z = 5*3 + 5*6 + 15*2 + 10*2 + 15*10 = 245

2. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

,.

Вводимо в цільову функцію множник лагранжа:

Z(x1,x3,λ)= + λ(7-2х1+2х2) Знаходимо похідні:

По х1: 6х1-2-2 λ

х2: 2х2-4+2 λ

λ: 7-2х1+2х2 Прирівнюємо похідні виражені через лямбда:

3х1-1=-х2+2 Звідси: х1=1,625; х2=-1,875; λ=2

Формуємо матрицю Гессе:

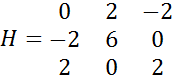
Визначаємо мінори 2-го та 3-го порядку: =-4 =-32 Маємо знакосталий ряд, що визначає нашу ф-цію на мінімум.Значення ЦФ=25,6875

Білет №27

1. Розв’язати транспортну задачу:

ai =(30;40;50); bj = (35; 30; 60);

.

де с_ij — вартість перевезення одиниці продукції від і -го постачальника до j -го споживача,

а_i — запаси продукції і -го постачальника; b_j — попит на продукцію j -го спо­живача.

Перевіряємо нашу задачу на збалансованість. Оскільки сумарний попит перевищує запаси, вводимо фіктивний склад:

Формуємо опорний план за методом північно-західного кута.

Значення функції: Z = 30*3+5*6+30*2+5*5+50*7+5*10=605

За методом Степінг-Стоун перебираємо всі допустимі плани задачі, формуючи цикли та здійснюючи перебір пустих клітинок у кожному плані. Приклад:

30-	+
5+	30-

σ = 1-3+6-2=2

Якщо значення сігма менше нуля, то існує кращий план і наявний можна поліпшити, за алгоритмом симплекс методу переходимо до нового плану. Процедуру повторюємо доти поки не знайдемо оптимальний план.

У даному випадку на 3-му етапі знаходимо оптимальний план:

Z = 30*2+30*2+10*5+35*5+15*7+5*10=510

3. Припустимо, що Вам надається можливість вибору тимчасової роботи по збуту продукції в двох різних місцях. Оплата праці на першому здійснюється на комісійних засадах: прибуток залежить від того, скільки Вам вдалося продати. На другому місці робота оплачується за ставкою. Існує ймовірність виходу фірми з бізнесу і тоді Ви отримаєте значно меншу заробітну плату як на першому, так і на другому місці роботи. Відповідні дані наведені в таблиці. Потрібно визначити, яке місце роботи найменш ризиковане.

Місце роботи	Результат 1	Результат 2
ймовірність	прибуток	ймовірність	прибуток
	0,5	3000 грн.	0,5	2000 грн.
	0,99	2510 грн.	0,01	1510 грн.

Щоб визначити ризик перемножимо відповідні ймовірності на прибутки в обох випадках і просумуємо:

0,5*3000 + 0,99*2510>0,5*2000+0,01*1510

Маємо: 3984,9>1015,1

Отже оскільки в першому випадку значення є більшим, то відповідний ризик буде меншим, ніж у другому випадку.

Екзамен.білет № 28

4.Розв’язати транспортну задачу:

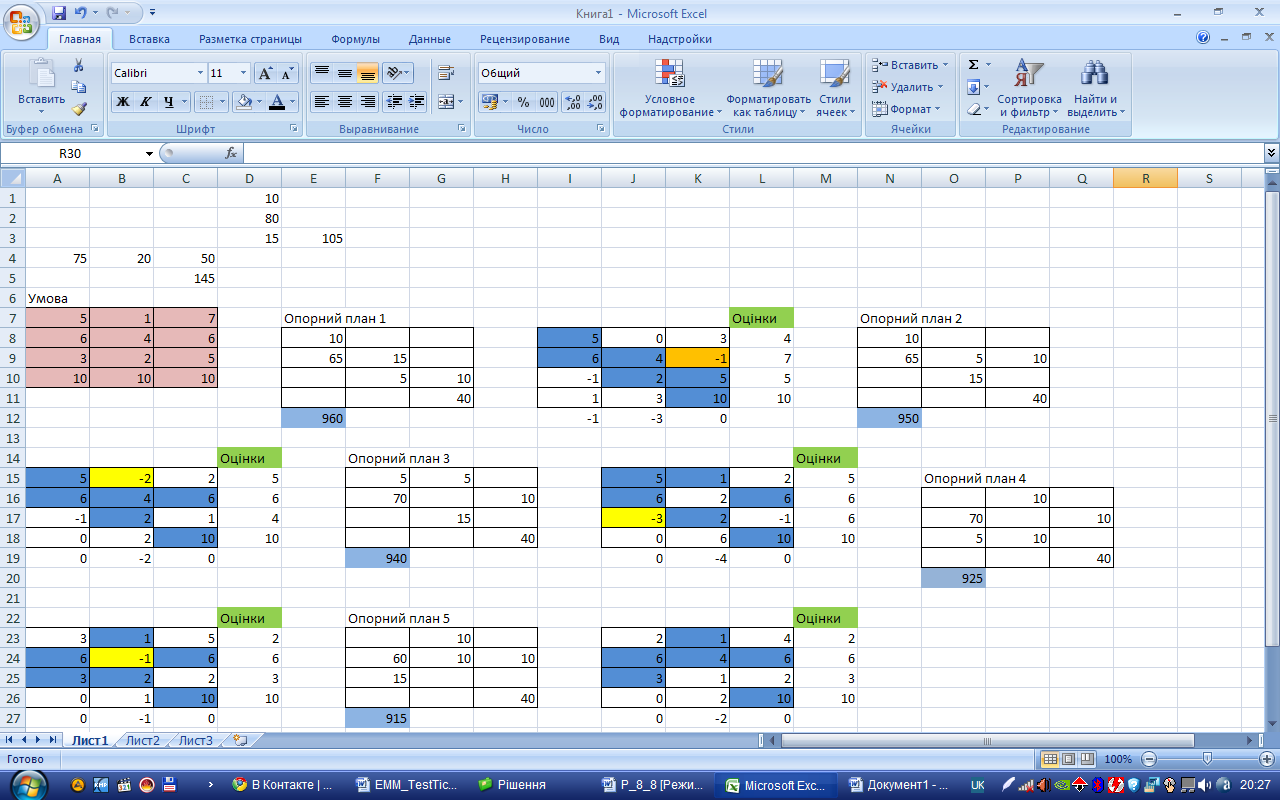
ai = (10; 80; 15); bj = (75; 20; 50);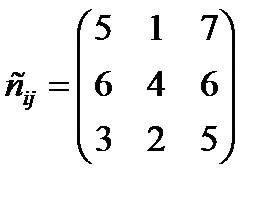

.

Задача розв.методом потенціалів. Початковий план знайдений методом Пн.-Зх. кута. Виділені ячейки вказують на значення, які переносяться з попереднього опорного плану, що відповідають табл., вказаній в умові відповідно. Задача не збалансована, тому вводиться фіктив.

5 .Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

, .

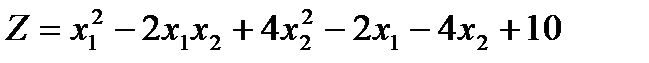Перетворюємо до вигляду Лагранжа:

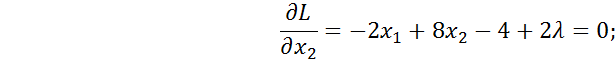
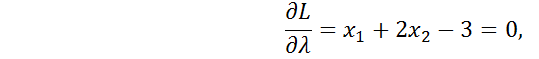
x1 = 3 – 2x2

2x2 – 2x1 + 2 = x1 – 4x2 + 2

2x2 – 6 + 4x2 + 2 = 3 – 2x2 – 4x2 +2

12x2 = 9

x1 = 1,5 x2 = 0,75

Знаходимо вид екстремуму:

Немає знакозмінного ряд, тому екстремум функції досягається у мінімумі. Значення функції: Z = 6.25

6. Орендне підприємство має можливість укласти дві різні угоди: першу угоду з фірмою в цьому ж місті, другу – з фірмою іншого міста, але з більш вигідними поставками. Можливі два варіанти прибутку при виборі першої фірми: 9000 гривень, якщо фірма буде мати змогу вкласти нову угоду, 7000 гривень, якщо це буде одинична поставка. При виборі другої фірми: 13000 гривень та 7500 гривень з урахуванням поставок. Результати та відповідні їм ймовірності наведені в таблиці. Вибрати найменш ризиковане рішення та оцінити величину ризику.

Дата добавления: 2015-10-31