Загальний марковський процес (Ланцюг Маркова з неперервним часом).

Визначення

Сімейство дискретних випадкових величин називається ланцюгом Маркова (неперервним часом), якщо:

.

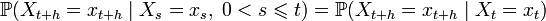Ланцюг Маркова з неперервним часом називається однорідним, якщо:

.

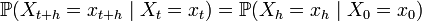92) Гранична поведінка перехідних ймовірностей ланцюга Маркова.

Стан i називається перехідним якщо, існує ненульова ймовірність, що починаючи з i, ми ніколи не повернемося в стан i. Більш формально нехай випадкова змінна T_i є часом першого повернення в стан i:

Тоді стан i є перехідним тоді й лише тоді, коли:

Якщо стан не є перехідним то він називається рекурентним. Неважко помітити, що якщо стан є перехідним то імовірність повернення в цей стан нескінченну кількість разів рівна нулю. У випадку рекурентного стану ця імовірність рівна одиниці. Тобто перехідний це такий стан, який процес в певний момент часу покидає назавжди, а рекурентний це такий стан до якого процес постійно повертається.

Визначимо також математичне очікування часу повернення:

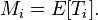
Для перехідного стану ця величина очевидно рівна нескінченності. Для рекурентних станів може бути як скінченним так і нескінченним. Стан i називається позитивно рекурентним, якщо M_i є скінченне; в іншому випадку i називається нуль-рекурентним.. Стан i є рекурентним тоді й лише тоді коли:

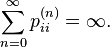
В одному класі досяжності або всі елементи є перехідними або всі елементи є рекурентними. Стан i називається поглинаючим якщо його неможливо покинути. Тобто:

93) Гілчастий процес.

Ветвящийся процесс — это случайный процесс, описывающий широкий круг явлений, связанных с размножением и превращением каких-либо объектов.

Основным аналитическим аппаратом ветвящихся процессов являются производящие функции:

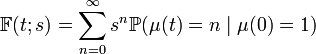
94) Алгебраїчний підхід вивчення скінченних ланцюгів Маркова.

95)

96) Випадковий проце, стаціонарний у широкому сенсі.

Випадковий процес Х (t) називають стаціонарним у широкому сенсі, якщо

m (t) = m (t + Δ), K (t, t ') = K (t + Δ, t' + Δ), (T € T, t '€ T, t + Δ € T), t' + Δ € T)

Очевидно, що з стаціонарності у вузькому сенсі слід стаціонарність у широкому сенсі.

З формул:

m (t) = m (t + Δ), K (t, t ') = K (t + Δ, t' + Δ), (T € T, t '€ T, t + Δ € T), t' + Δ € T)

Слід, що для процесу, стаціонарного в широкому сенсі, можна записати

m (t) = m _x (0) = const; D (t) = K (t, t) = K (0,0) = const; K (t, t ') = K (t - t', 0) = K (0, t '- t)

Таким чином, для процесу, стаціонарного в широкому сенсі, математичне очікування і дисперсія не залежать від часу, а K (t, t ') являє собою функцію вида:

K (t, t ') = k (τ) = k (- τ), τ = t' - t.

Видно, що k (τ) - парна функція, при цьому

K (0) = В = σ ^2; | k (τ) | ≤ k (0); Σ Σ ά _i α _j k (t _i - t _j) ≥ 0

Тут D - дисперсія стаціонарного процесу

Х (t), α _i (I = 1, n) - довільні числа.

97) Аналіз кореляційної функції. Ергодичність.

Кореляційний аналіз – це статистичне дослідження (стохастичної) залежності між випадковими величинами (англ. correlation – взаємозв’язок). У найпростішому випадку досліджують дві вибірки (набори даних), у загальному – багатовимірні комплекси (групи) геологічних параметрів або об’єктів.

Мета кореляційного аналізу – забезпечити отримання деякої інформації про одну змінну за допомогою іншої змінної. В випадках, коли можливе досягнення мети, говорять, що змінні корелюють. В загальному вигляді сприйняття гіпотези про наявність кореляції означає, що зміна значення змінної А відбудеться одночасно з пропорційною зміною значення В.

Мірою залежності між експериментальними наборами даних є числа – коефіцієнти зв’язку.

Головні завдання кореляційного аналізу:

1) оцінка за вибірковими даними коефіцієнтів кореляції;

2) перевірка значущості вибіркових коефіцієнтів кореляції або кореляційного відношення;

3) оцінка близькості виявленого зв’язку до лінійного;

4) побудова довірчого інтервалу для коефіцієнтів кореляції.

Визначення сили та напрямку взаємозв’язку між змінними є однією з важливих проблем аналізу даних. В загальному випадку для цього застосовують поняття кореляції.

Ергоди́чність — спеціальна властивість деяких (динамічних) систем, яка полягає в тому, що в процесі еволюції такої системи майже кожна точка її з певною ймовірністю проходить поблизу будь-якої іншої точки системи. Тоді при розрахунках час, який важко розраховувати, можна замінити фазовими (просторовими) показниками. Система, в якій фазові середні збігаються з часовими, називається ергодичною.

98)

99)

100) Рівняння Колмогорова - Чепмена

Рівняння Колмогорова - Чепмена для однопараметричного сімейства безперервних лінійних операторів в топологічному векторному просторі виражає напівгрупова властивість:

Найчастіше цей термін використовується в теорії однорідних марківських випадкових процесів, де - Оператор, що перетворює розподіл ймовірностей в початковий момент часу в розподіл ймовірності в момент часу ().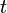

Для неоднорідних процесів розглядаються двохпараметричного сімейства операторів 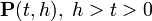, Перетворюючих розподіл ймовірностей в момент часу в розподіл ймовірності в момент часу Для них рівняння Колмогорова-Чепмена має вигляд

Для систем з дискретним часом параметри приймають натуральні значення.

Дата добавления: 2015-10-31