Помилки першого та другого роду.

При перевірці статистичної гіпотези за даними вибірки можна зробити хибний висновок (похибки 1 та 2 роду).

Якщо неправильна гіпотеза відкинута, то це похибка 1 роду.

Якщо неправильна гіпотеза буде прийнята, то це похибка 2 роду.

Імовірність здійснити похибку першого роду назив рівнем значущості 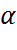, 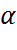задається наперед і в більшості випадків 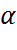= 0,05,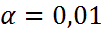

Імовірність здійснити похибку другого роду позначається - прийняти неправильну гіпотезу. Імовірність (1 – ) – не допустити похибку другого роду. Тобто відкинути неправильну гіпотезу назив потужністю критерію.

75. Статистичний критерій. Критична область.

Для перевірки правильності висунутої статистичної гіпотези вибирають так званий статистичний критерій, керуючись яким відхиляють або не відхиляють нульову гіпотезу. Статистичний критерій, котрий умовно позначають через K, є випадковою величиною, закон розподілу ймовірностей якої нам заздалегідь відомий. Так, наприклад, для перевірки правильності як статистичний критерій K можна взяти випадкову величину, яку позначають через K = Z, що дорівнює 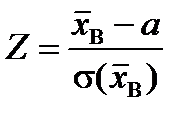і яка має нормований нормальний закон розподілу ймовірностей. При великих обсягах вибірки (n > 30) закони розподілу статистич­них критеріїв наближатимуться до нормального. Спостережуване значення критерію, який позначають через K ^*, обчислюють за результатом вибірки.

Множину W всіх можливих значень статистичного критерію K можна поділити на дві підмножини А і , які не перетинаються. . Сукупність значень статистичного критерію K Î А, за яких нульова гіпотеза не відхиляється, називають областю прийняття нульової гіпотези. Сукупність значень статистичного критерію K Î , за яких нульова гіпотеза не приймається, називають критичною областю. Отже, А — область прийняття Н ₀, — критична область, де Н ₀ відхиляється. Точку або кілька точок, що поділяють множину W на підмножини А і , називають критичними і позначають через K _кр. Існують три види критичних областей: Якщо при K < K _крнульова гіпотеза відхиляється, то в цьому разі ми маємо лівобічну критичну область, яку умовно можна зобразити (рис. 1).

Якщо при нульова гіпотеза відхиляється, то в цьому разі маємо правобічну критичну область

Якщо ж при і при нульова гіпотеза відхиляється, то маємо двобічну критичну область

Лівобічна і правобічна області визначаються однією критичною точкою, двобічна критична область — двома критичними точками, симетричними відносно нуля.

76. Дати означення моделі експерименту.

Випадковий експеримент (випадкове випробування, випадковий досвід) - математична модель відповідного реального експерименту, результат якого неможливо точно передбачити. Математична модель повинна задовольняти вимогам: вона повинна бути адекватна і адекватно описувати експеримент; повинна бути визначена сукупність безлічі спостережуваних результатів в рамках розглянутої математичної моделі при строго певних фіксованих початкових даних, що описуються в рамках математичної моделі; повинна існувати принципова можливість здійснення експерименту з випадковим результатом наскільки угодне кількість разів при незмінних вхідних даних, (де - кількість вироблених експериментів); повинно бути доведено вимогу або апріорі прийнята гіпотеза про стохастичною стійкості відносної частоти для будь-якого спостережуваного результату, визначеного в рамках математичної моделі.

77. Дати поняття одно факторний аналіз.

Дисперсійний аналіз дає загальну схему перевірки статистичних гіпотез, що базуються на вивченні різних джерел варіації або неоднорідності. Однофакторний дисперсійний аналіз використовується для перевірки значимих відмінностей між середніми значеннями вибірок, що розглядаються. Дані аналізу – це k незалежних одновимірних вибірок, елементи яких вимірюються в однакових одиницях. Кількість елементів кожної вибірки може бути різною. Однофакторний аналіз порівнює 2 джерела варіації: - міжгрупова (між вибірками), -внутрішньогрупова (в середині однієї вибірки).

Нехай потрібно дослідити вплив на ознаку Х певного одного фактора. Результати експерименту ділять на певне число груп, які відрізняються між собою ступенем дії фактора.

Для зручності в проведенні необхідних обчислень результати експерименту зводять в спеціальну таблицю:

Ступінь впливу фактора (групи)	Спостережуване значення ознаки Х	Групові середні	Загальна середня
			,
….	…	…
р

78. Загальна дисперсія, між групова та внутрішньогрупова дисперсії.

Міжгрупова дисперсія – дисперсія групових середніх, зумовлена впливом досліджуваного фактора на ознаку х.

Внутрішньогрупова дисперсія – дисперсія, зумовлена впливом інших випадкових факторів.

Загальна дисперсія розглядається як сума квадратів відхилень для того, щоб мати виправлені дисперсії, їх називають залишковою та факторною, необхідно кожну із здобутих сум поділити на число ступенів свободи.

S²_зал. =

S²_факт. =

79. Загальний метод перевірки впливу фактора на ознаку способом порівняння дисперсій

Завдання виявлення впливу фактора на наслідки експерименту полягає в порівнянні виправлених дисперсій , . І справді, якщо досліджуваний фактор не впливає на значення ознаки Х, то в цьому разі і можна розглядати як незалежні оцінки загальної дисперсії D. І навпаки, якщо відношення i істотне, то в цьому разі вибірки слід вважати здійсненими з різних сукупностей, тобто з сукупностей з різним рівнем впливу фактора.

Порівняння двох дисперсій ґрунтується на перевірці правильності нульової гіпотези: — про рівність дисперсій двох вибірок.

За статистичний критерій вибирається випадкова величина ,

що має розподіл Фішера—Снедекора з , ступенями свободи.

За значеннями a, , , знаходимо критичну точку (додаток 7).

Спостережуване значення критерію обчислюється за формулою

Якщо , то нульова гіпотеза про вплив фактора на результати досліджень відхиляється, а коли , то цим самим підтверджується вплив фактора на ознаку Х.

Результати спостережень та обчислення статистичних оцінок зручно подати в упорядкованому вигляді за допомогою табл. 2

80. Поняття про функціональну, статистичну та кореляційну залежності.

Показником, що вимірює стохастичний зв’язок між змінними, є коефіцієнт кореляції, який свідчить з певною мірою ймовірності, наскільки зв’язок між змінними близький до строгої лінійної залежності.

За наявності кореляційного зв’язку між змінними необхідно виявити його форму функціональної залежності (лінійна чи нелінійна), а саме: ;

;

Наведені можливі залежності між змінними X і Y називають функціями регресії. Форму зв’язку між змінними X і Y можна встановити, застосовуючи кореляційні поля, які зображені на рисунках

Для двовимірного статистичного розподілу вибірки ознак (Х, Y) поняття статистичної залежності між ознаками Х та Y має таке визначення:

статистичною залежністю Х від Y називають таку, за якої при зміні значень ознаки Y = y_i змінюється умовний статистичний розподіл ознаки Х, статистичною залежністю ознаки Y від Х називають таку, за якої зі зміною значень ознаки X = x_i змінюється умовний статистичний розподіл ознаки Y.

Між ознаками Х та Y може існувати статистична залежність і за відсутності кореляційної. Але коли існує кореляційна залежність між ознаками Х та Y, то обов’язково між ними існуватиме і статистична залежність.

81.Рівняння лінійної регресії. Довірчий інтервал для лінії регресії

Якщо дано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку економетричну модель, яка б найкраще описувала існуючу залежність. Одним з методів є лінійна регресія. Лінійна регресія передбачає побудову такої прямої лінії, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю пряму одержуємо значення прогнозу. Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої. В загальному вигляді рівняння прямої виглядає:

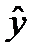=а+bх, (1.1)

де ­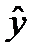- вирівняне значення у для відповідного значення х.

Константи а і b - константи, які передбачають зменшення суми квадратів відхилень між фактичним значенням у і вирівняним значенням .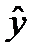

S(у - 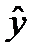)2 ® min (1.2)

Коефіцієнт а характеризує точку перетину прямої регресії з лінією координат.

Коефіцієнт b характеризує кут нахилу цієї прямої до осі абсцис, а також на яку величину зміниться 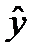при зміні х на одиницю.

Коефіцієнти а і b знаходять із системи рівнянь (1.3), що випливає з формули (1.2).

(1.3)

Знайшовши значення параметрів розраховують ряд вирівняних значень для відповідних факторів і проводять дослідження знайденої економетричної моделі.

Щоб зробити висновок про доцільність використання знайденої моделі проводять аналіз за наступними напрямками:

1) Розраховують критерій Фішера та перевіряють знайдену модель на адекватність вихідним даним;

2) Розраховують і аналізують дисперсію показників;

3) Розраховують і аналізують коефіцієнт кореляції;

4) Розраховують та аналізують коефіцієнт еластичності;

5) Розраховують довірчий інтервал для прогнозованих показників.

Довірчий інтервал.

Вихідна економетрична модель лінійної регресії передбачає наявність випадкової величини Е, яка вимірює похибку між фактичним значенням і вирівняним значенням показника. Для розрахунку цих похибок використовують поняття "стандартного відхилення"

, (1.13)

де Sr – стандартна похибка рівняння регресії

n-2 – число значень ряду зменшене на кількість параметрів рівняння регресії (тобто а і b).

Розрахувавши стандартну похибку рівняння регресії знаходимо стандартну похибку прогнозу:

(1.14)

Для розрахунку довірчих меж потрібно знайти значення .

Нижня межа довірчого інтервалу ; верхня межа довірчого інтервалу .

Прогнозне значення ур=a+bxp буде знаходитись в межах від уmin до ymax.

(1.15)

де t – критерій Стюдента (знаходиться з таблиць в залежності від ймовірності P і ступеня вільності n-m-1).

82.Вибірковий коефіцієнт кореляції.

Рівняння лінійної парної регресії:

або

,

де і називають коефіцієнтом регресії. Для обчислення необхідно знайти

;

;

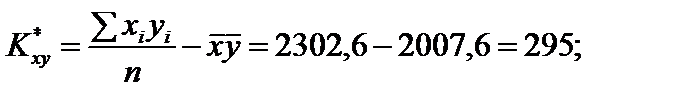
Як бачимо, коефіцієнт кореляції близький за своїм значенням до одиниці, що свідчить про те, що залежність між Х та Y є практично лінійною.

83.Множинна регресія, множинний коефіцієнт кореляції та його властивості.

Регресія (рос. регрессия, англ. regression; нім. Regression f) — форма зв'язку між випадковими величинами. Закон зміни математичного очікування однієї випадкової величини залежно від значень іншої. Розрізняють прямолінійну, криволінійну, ортогональну, параболічну та інші регресії, а також лінію і площину регресії.

Крива регресії Y на Х є залежність умовного математичного очікування величини Y від заданого значення Х:

my/x = φ (х, а, b, c, …),

де а, b, c, … — параметри рівняння регресії.

Регресія дозволяє за величиною однієї ознаки (змінна x) знаходити середні (очікувані) значення іншої ознаки (змінна У), зв'язаної з x кореляційно. Оскільки в дослідженнях конкретний вид взаємозв'язків невідомий, одне з головних завдань регресійного аналізу полягає у доборі відповідного виразу У = / (X), графік якого проходить через емпіричні точки (або досить близько до них) і таким чином зв'язує змінні x і У.

Множинна регресія - це оцінювання, наприклад, змінної У лінійною комбінацією т незалежних зміннихх1,х2, хт. Найпростіший варіант регресії має місце для т=2, коли необхідно спрогнозувати залежність однієї змінної У від двох змінних х1 і Х2. Рівняння такої множинної регресії має вигляд:

? = Бх ■ X! + Б2 ■ X2 + Б0,

де Б1 = Ь1 o Зу/^; Б2 = Ь2 ■ $у/$г;, Б0 = У - Ах■ X1 - А2 o X2;

Ь1 = (Гу1 ~ Гу2 o Г12)/(1 - Г122); Ь2 = (Гу2 " Гу1 ' Г12)/(1 " ^2)

зу, з1, з2, У, X1, X2 - стандартні відхилення і середні значення У, х1 і х2; Гу1, Гу2, г12 - коефіцієнти парної кореляції Пірсона між У і Х1, У і Х2, Х1 і Х2. Для оцінювання зв'язку, з одного боку, змінної У, а з іншого - двох змінних Х1 і Х2, використовують коефіцієнт множинної кореляції:

Ку-1,2 =д/Ь1 o Гу1 + Ь2 o Гу2.

Множинний коефіцієнт кореляції

Множинний коефіцієнт кореляції визначається тоді, коли на дану ознаку

одночасно комплексно впливають дві інших ознаки (фактора) X i Z. В таких

випадках визначається не парний (по 2-х ознаках), а сукупний коефіцієнт

кореляції для 3-х ознак − X, Y, Z:

На відміну від парних коефіцієнтів кореляції сукупний коефіцієнт кореляції має лише позитивне значення.

Іноді необхідно при трьох взаємообумовлюючих факторах виявити взаємовплив лише для двох з них. Тоді застосовується коефіцієнт парціальної кореляції для обраних двох факторів (ознак). Це частинний (частковий) або парціальний коефіцієнт кореляції:

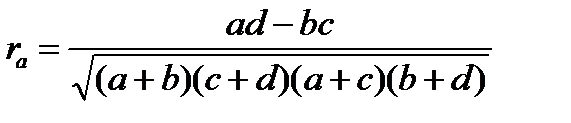
Відповідно

84.Нелінійна регресія.

Якщо в рівняння множинної регресії змінні входять як , то регресія називається нелінійною.

У загальному випадку нелінійна регресія записується в такому вигляді:

де параметри є сталими невідомими величинами, які підлягають статистичним оцінкам, а 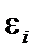— випадкова величина, яка має нормальний закон розподілу з числовими характеристиками і при цьому випадкові величини між собою не корельовані.

85) Визначення та приклади ланцюгів Маркова.

Ланцюг Маркова в математиці це випадковий процес, що задовольняє властивість Маркова і який приймає скінченну чи зліченну кількість значень (станів). Існують ланцюги Маркова як з дискретним так і з неперервним часом. В даній статті розглядається дискретний випадок.

Інтуїтивне визначення

Нехай I -деяка скінченна чи зліченна множина елементи якої називаються станами. Нехай деякий процес в момент часу n (де n =0,1,2,3…) може перебувати в одному із цих станів, а в час n+1 перейти в деякий інший стан(чи залишитися в тому ж). Кожен такий перехід називається кроком. Кожен крок не є точно визначеним. З певними ймовірностями процес може перейти в один з кількох чи навіть усіх станів. Якщо імовірності переходу залежать лише від часу n і стану в якому перебуває процес в цей час і не залежать від станів в яких процес перебував у моменти 0, 1, …, n-1 то такий процес називається (дискретним) ланцюгом Маркова. Ланцюг Маркова повністю задається визначенням ймовірностей p_i перебування процесу в стані в час n=0 і ймовірностей переходу зі стану в стан в час n. Якщо ймовірності переходу не залежать від часу (тобто однакові для всіх n) то такий ланцюг Маркова називається однорідним. Саме однорідні ланцюги Маркова є найважливішими на практиці і найкраще вивченими теоретично. Тому саме їм приділятиметься найбільша увага у цій статті.

Дата добавления: 2015-10-31