Формальне визначення

Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо

.

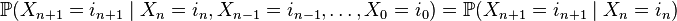Тобто майбутні значення послідовності залежать лише від теперішнього стану і не залежать від минулих.

Матриця , де

називається ма́трицею ймовірностей переходу на -му кроці, а вектор , де

— початковим розподілом ланцюга Маркова.

Очевидно, матриця ймовірностей переходу є стохастичною, тобто

.

Ланцюг Маркова називається однорідним якщо:

,

або еквівалентно:

для всіх n.

Граф переходів ланцюга Маркова

Поширеним способом візуального задання ланцюга Маркова є граф переходів. Вершини цього графа ототожнюються зі станами ланцюга Маркова, а орієнтовне ребро проходить з вершини i у вершину j проходить лише у випадку коли імовірність переходу між відповідними станами нерівна нулю. Дана ймовірність переходу також позначається біля відповідного ребра.

Приклад

Розглянемо основні дії з ланцюгами Маркова на наступному прикладі:

Візьмемо початковий розподіл:

Після першого кроку одержимо роподіл:

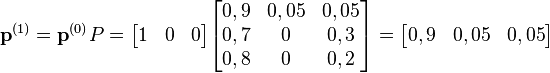
Після двох кроків одержиться наступний розподіл:

Далі можна продовжити за формулами:

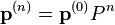
Оскільки даний ланцюг Маркова є нерозкладний і аперіодичний існує єдиний граничний розподіл :

Його можна знайти за такими формулами:

З умови ,одержується єдиний результат:

86) Ймовірність переходу за n кроків.

Нехай маємо однорідний ланцюг Маркова з матрицею ймовірностей переходу P. Позначимо:

Оскільки ланцюг Маркова є однорідним то дане означення не залежить від n. Тоді виконується рівність

де 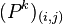— елемент i -го рядка і j -го стовпчика матриці P^k.

87) Замкнуті множини станів.

За́мкнута множина́ — підмножина простору доповнення до якої відкрита.

Означення

Нехай дано топологічний простір. Множина називаєтся замкнутою відносно топології , якщо існує відкрита множина така що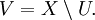

Властивості

Із аксіом означення топології випливає:

· перетин будь-якого набору замкнутих множин є замкнутою множиною

· об'єднання скінченної кількості замкнутих множин є замкнутою множиною

88) Класифікація станів. Неповоротний стан.

Класифікація станів:

Дата добавления: 2015-10-31