Системы координат. Углы Эйлера.

В качестве основных обычно рассматривают неподвижную и связанную системы координат. Неподвижная (земная) 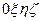система координат привязана к какой-либо точке 0 на земле и ориентирована осью на север (или на заданный курс); оси - ортогональны и лежат в плоскости местного горизонта, а - направлена вверх (иногда вниз).

Рис.2

Связанная система координат привязана к геометрическому центруОМТ (обычно к центру величины или масс), а оси совпадают с главными центральными осями инерции. Ось лежит в диаметральной плоскости и направлена в нос (для большинства ОМТ, как то корабль, ПЛ, торпеда и пр.), ось также лежит в диаметральной плоскости и направлена вверх, а ось перпендикулярна плоскости .

Возможна также промежуточная или полусвязанная система координат, которая характеризуется тем, что ее начало всегда совмещено с центром масс ОМТ, а координатные оси либо параллельны осям неподвижной системы координат, либо развернуты в горизонтальной плоскости на угол заданного курса (в такой системе удобнее рассматривать рыскание ОМТ на курсе).

Следует отметить, что в задачах синтеза законов управления до настоящего времени практически не учитывались особенности формирования управляющих сил для соответствующих систем координат (в которых действуют исполнительные органы). Пример: закон управления глубиной принятый на многих объектах формирует управление в связанной системе по замерам параметров движения в неподвижной (без соответствующего пересчета параметров движения в связанную систему координат).

Обозначения кинематических параметров Табл.1

Степень свободы	Вид движения в связ СК	Силы и моменты в связ. СК	Линейные и угловые скорости в связ. СК	Линейные и угловые (Эйлера) координаты в неподв.СК
	Вдоль оси 0х
	Вдоль оси 0у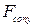
	Вдоль оси 0z
	Вращ. Вокруг 0х
	Вращ. Вокруг 0у
	Вращ. Вокруг 0z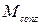

В дальнейшем вектор линейных и угловых координат в неподвижной системе координат обозначаем 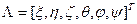. Иногда будем выделять вектор линейных перемещений 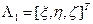и вектор ориентации (углы Эйлера) .

Совокупный вектор линейных и угловых скоростей в связанной системе будем обозначать , ()а вектор управляющих сил и моментов (в связанной системе координат) - .

Примеры векторно-матричного представления систем и объектов. Системы ДУ.

Структура принятой формы записи уравнений динамики и кинематики (без учета ветро-волновых сил):

(1)

Углы Эйлера

Линейные перемещения МПО относительно неподвижной системы (earth-fixed) координат определяется преобразованием вектора скорости

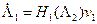, обратное преобразование .

Аналогично , .

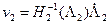И в общем случае , .

Теоремы Эйлера о вращении. Единичные повороты.

Пусть один и тот же вектор зафиксирован в системе (неподвижной) и как вектор в системе (связанной).

Система развернута по отношению к системе на угол относительно оси вращения, положение которой задано единичным вектором 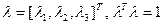в неподвижной с.к., рис.3.

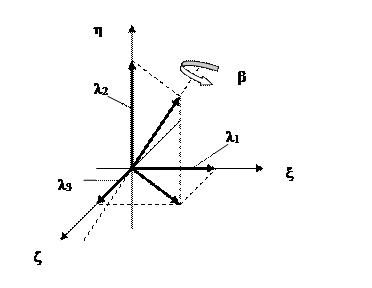
Рис.3

Тогда вектор может быть выражен [4] соотношением

Переход от вектора к вектору в матричной форме имеет вид

, где 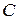- матрица вращения, м.б. получена заменой единичной матрицей. Тогда

, где (2)

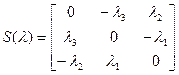-кососимметрическая матрица.

определяется следующим образом

- 1-й столбец матрицы ;

- 2-й столбец матрицы ;

- 3-й столбец матрицы .

Матрица называется кососимметрической, т.к. .

.

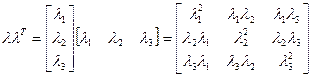Тогда

. (2)

Матрица С состоит из следующих элементов

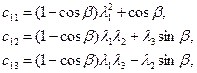
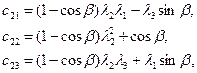(3)

И удовлетворяет соотношениям .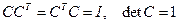

Дата добавления: 2015-10-31