Понятие кватерниона

Кватернион представляет собой вектор 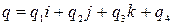, сформированный 3-мя ортогональными векторами и 1 и с использованием чисел .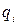

Используем соотношение (2)

Параметры Эйлера или единицу кватернионов определим как

,

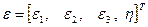причем вектор связан с параметрами Эйлера соотношениями:

; , .

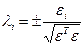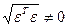Соответственно .

Параметры Эйлера удовлетворяют соотношению

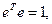или .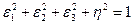

Тогда элементы матрицы 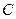определяются из соотношений:

.

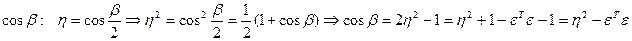
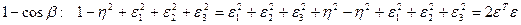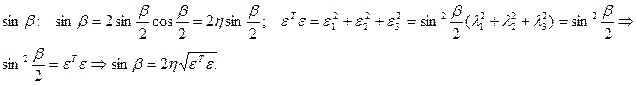
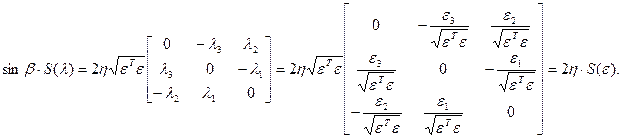
Преобразующая матрица для параметров Эйлера в этом случае имеет вид:

()

Составляющие матрицы :

,

, .

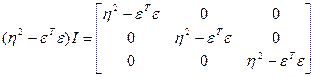Преобразование линейных скоростей.

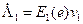, (скорости 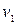постоянно измеряются)

где 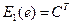, тогда

, (8)

. Уравнения для вектора приводятся ниже.

Преобразование угловых скоростей.

Матрица 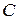удовлетворяет соотношению

.

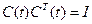Продифференцировав, получим

.

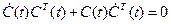Обозначим 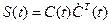- любая кососимметрическая матрица,т.е. ),

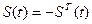Домножив обе части ур-ния на 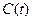, тогда получим (с учетом, что )

,

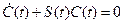Пусть .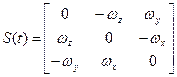

Тогда предыдущее уравнение можно раскрыть

.

Подстановка в уравнение параметров 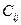из уравнения () (выше для С) приводит к уравнению для вычисления вектора

,

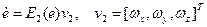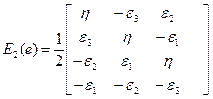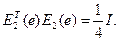, (9)

Соответственно кинематические уравнения движения можно записать в виде

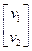
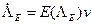. (10)

,

Алгоритм вычисления параметров Эйлера

1. 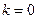. Вычисляются (или определяются по GPS) начальные значения 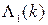и (см.ниже).

2. Методом Эйлера вычисляются значения переменных на следующем шаге

- шаг интегрирования.

3. Нормализация:

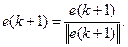
4. -приращение переменной 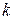и возврат к п.2.

Связь между параметрами Эйлера и углами Эйлера

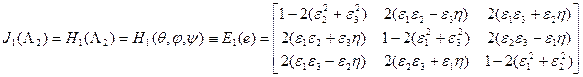
или

.

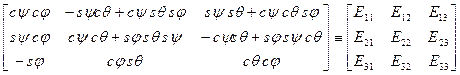Откуда

(11)

где - вычисляется в четвертом квадранте для вещественных 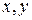по формуле

,

.

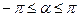Вычисление начальных условий для интегрирования уравнений для параметров Эйлера

Может осуществляться на основании замеренных в начальный момент углов Эйлера:

Возможны два способа:

1-й способ:

Поскольку

то , .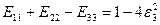

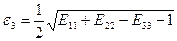С последующей нормировкой параметров .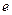

Й способ.

1. Предположим, углы Эйлера известны. Тогда матрица преобразования , соответствующая этим величинам имеет вид

.

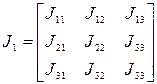2. След матрицы 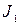вычисляется по ф-ле

3. Пусть, для 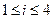есть индекс 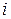,соответствующий

.

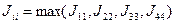4. Определим

.

Знак 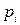м.б. выбран положительным или отрицательным.

5. Вычислим другие три величины 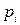по формулам

Например, выбран параметр 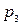, тогда используются уравнения, содержащий этот параметр.

6. Вычислить параметры 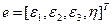из соотношений

Дата добавления: 2015-10-31