Варіанти 25-30.

Радіоприймач приймає сигнал з імовірністю р. Побудувати ряд розподілу, функцію розподілу. Знайти ймовірність того, що з N сигналів, буде прийнято: а) не більше M сигналів; б) два сигнали. Знайти математичне сподівання й дисперсію випадкової величини - числа прийнятих сигналів, якщо було передано N сигналів. Знайти найбільш імовірне число принятіх сигналів, якщо передано N сигналів

Вар.
р	0,3	0,6	0,4	0,5	0,6	0,5
N
М

ЗАДАЧА 5

Дана щільність розподілу неперервної випадкової величини .

Знайти: 1) коефіцієнт; 2) функцію розподілу; 3) математичне сподівання, дисперсію та середнє квадратичне відхилення випадкової величини; 4) ймовірність попадання випадкової величини в інтервал.

Номер завдання віподвідає номеру варіанту.

1. .

3. .

5. .

7. .

10. .

11. .

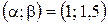12. .

13. .

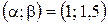14. .

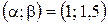15. .

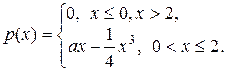
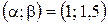16. .

17. .

18. .

19. .

20. .

21. .

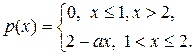
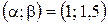23. .

Варіанты 2,4,6,8,9,22,24

Дана функція розподілу 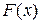неперервної випадкової величини .

Знайти: 1) щільність розподілу ;2) коефіцієнт 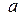;3) математичне сподівання , дисперсію випадкової величини 5) ймовірність попадання випадкової величини в інтервал .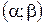

2.

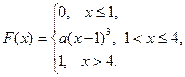
4.

6.

8.

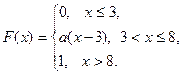
9.

22.

24.

Варіанты 25-30.

Дана щільність розподілу неперервної випадкової величини .

Знайти: 1) параметр A; 2) функцію розподілу; 3) математичне сподівання, дисперсію та середнє квадратичне відхилення випадкової величини; 4) ймовірність попадання випадкової величини в інтервал.5) Побудувати функцію розподілу.

Р{0 < < a/2 }

вар.
а

ЗАДАЧА 6

1. Випадкова величина Х задана функцією розподілу

Знайти ймовірність того, що в результаті чотирьох незалежних випробувань величина Х рівно три рази прийме значення, що належить інтервалу (0,25, 0,75).

2. Ціна певного цінного паперу нормально розподілена. Протягом останнього року 20% робочих днів вона була нижче 88 ден. од., а 75% - вище 90 ден. од. Знайти: а) математичне сподівання і середнє квадратичне відхилення ціни цінного паперу.
3. Коробки з цукерками упаковуються автоматично. Їх середня маса дорівнює 540 р. Відомо, що маса коробок з цукерками має нормальний розподіл, а 5% коробок мають масу, меншу 500 г. Який відсоток коробок, маса яких: а) менше 470 г, б) від 500 до 550 г?

3. Точність виготовлення деталей характеризується систематичною помилкою 2 мм, а випадкове відхилення розподілено за нормальним законом з середньою квадратичною помилкою 10 мм. Яка ймовірність, що відхилення довжини виробу від стандарту знаходиться в межах від 8 до 12 мм?

4. Середній час безвідмовної роботи приладу дорівнює 80 год Вважаючи, що час безвідмовної роботи приладу має показовий закон розподілу, знайти: а) вираз його щільності ймовірності та функції розподілу; б) ймовірність того, що протягом 100 год прилад не вийде з ладу.

5. Час виготовлення деталі розподілено по нормальному закону з математичним очікуванням 5,8 с і середньоквадратичним відхиленням 1,9 с. Яка ймовірність, що для виготовлення деталі буде потрібно від 5 до 7 с?

6. Імовірність виграшу по облігації позики за весь час його дії дорівнює 0,1. Скласти закон розподілу числа виграли облігацій серед придбаних 19. Знайти математичне сподівання, дисперсію, середнє квадратичне відхилення цієї випадкової величини.

7. Випадкова величина Х задана щільністю розподілу f (х) =0, 5 х в інтервалі (0;2); поза цим інтервалом f (х) =0. Знайти початкові й центральні моменти першого, другого, третього й четвертого порядків.

8. Максимальна швидкість літаків певного типу розподілена по нормальному закону з математичним очікуванням 420м / с і середньоквадратичним відхиленням 25 м / с. Знайти ймовірність того, що під час випробування літака цього типу його максимальна швидкість буде змінюватися від 390 м / с до 440 м / с

9. Випадкова величина Х задана щільністю розподілу f (х) =2 х в інтервалі (0;1); поза цим інтервалом f (х) =0. Знайти початкові й центральні моменти першого, другого, третього й четвертого порядків.

10. Знайти математичне сподівання, дисперсію й середнє квадратичне відхилення випадкової величини Х, рівномірно розподіленої в інтервалі (2;8).

11. Знайти математичне сподівання, дисперсію й середнє квадратичне відхилення випадкової величини Х, рівномірно розподіленої в інтервалі (3;5).

12. Прилад для вимірювання висоти має систематичну помилку 15 м і середню квадратичну помилку 10 м. Знайти ймовірність того, що помилка за абсолютною величиною не буде більше 20 м. Закон розподілу помилок нормальний.

13. Деталь приймається ВТК, якщо її діаметр відхиляється за абсолютною величиною від стандартного не більше ніж на 2 мм. Відхилення - випадкова величина, розподілена нормальному закону з систематичною помилкою 0,5 мм і середньоквадратичним відхиленням 1 мм. Знайти ймовірність того, що деталь приймається

14. Математичне сподівання й середнє квадратичне відхилення нормально розподіленої випадкової величини Х відповідно дорівнюють 10 і 2. Знайти ймовірність того, що в результаті випробування Х прийме значення, укладене в інтервалі (12,14).

15. Математичне сподівання й середнє квадратичне відхилення нормально розподіленої випадкової величини Х відповідно дорівнюють 20 і 5. Знайти ймовірність того, що в результаті випробування Х прийме значення, укладене в інтервалі (15,25).

16. Ціна певної цінного паперу нормально розподілена. Протягом останнього року 20% робочих днів вона була нижче 88 ден. од., а 75% - вище 90 ден. од. Знайти ймовірність того, що в день покупки ціна буде укладена в межах від 83 до 96 ден. од.

17. Знайти щільність і функцію розподілу показового закону, якщо параметр λ =7.

18. Неперервна випадкова величина Х розподілена за показовим законом, заданим щільністю ймовірності f (х) =3 е^{- 3 х} при х ≥0; при х <0 f (х) =0. Знайти ймовірність того, що в результаті випробування Х попадає в інтервал (0,13;0,7).

19. Неперервна випадкова величина Х розподілена за показовим законом, заданим щільністю ймовірності f (х) =0, 04 е^{- 0, 04 х} при х ≥0; при х <0 f (х) =0. Знайти ймовірність того, що в результаті випробування Х попадає в інтервал (1;2).

20. Випадкова величина Х задана функцією розподілу

Знайти ймовірність того, що в результаті випробування величина Х прийме значення: а) менше 0,2; б) менше трьох; в) не менше трьох; г) не менше п'яти.

21. Випадкова величина Х задана функцією розподілу

Знайти ймовірність того, що в результаті чотирьох незалежних випробувань величина Х рівно три рази прийме значення, що належить інтервалу (0,25, 0,75).

22. Скласти функцію розподілу випадкової величини, що має біноміальний закон розподілу з параметрами n і р.

23. Ціна ділення шкали вимірювального приладу дорівнює 0,2. Показання приладу округляють до найближчого цілого числа. Вважаючи, що при відліку помилка округлення розподілена за рівномірним законом, знайти: 1) математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини; 2) ймовірність того, що помилка округлення: а) менше 0,04; б) більше 0,05.

24. Поточна ціна акції може бути змодельована за допомогою нормального закону розподілу з математичним очікування 15 ден. од. і середнім квадратичним відхиленням 0,2 ден. од. 1. Знайти ймовірність того, що ціна акції: а) не вище 15,3 ден. од.; б) не нижче 15,4 ден. од.; в) від 14,9 до 15,3 ден. од..

25. Ціна певного цінного паперу нормально розподілена. Протягом останнього року 20% робочих днів вона була нижче 88 ден. од., а 75% - вище 90 ден. од. Знайти з надійністю 0,95 визначити максимальне відхилення ціни цінного паперу від середнього (прогнозного) значення (за абсолютною величиною)

26. Коробки з цукерками упаковуються автоматично. Їх середня маса дорівнює 540 р. Відомо, що маса коробок з цукерками має нормальний розподіл, а 5% коробок мають масу, меншу 500 г. Який відсоток коробок, маса яких: 1) відрізняється від середньої не більше, ніж на 30 г (за абсолютною величиною) 2) більше 500г?

27. Випадкова величина X має нормальний розподіл з математичним очікуванням а = 25. Ймовірність попадання Хв інтервал (10, 15) дорівнює 0,09. Чому дорівнює ймовірність попадання X в інтервал: а) (35, 40), б) (30, 35)?

28. Час ремонту телевізора розподілено за показовим законом з математичним очікуванням, рівним 0,5 ч. Хтось здає в ремонт два телевізори, які одночасно починають ремонтувати, і чекає, коли буде відремонтовано один з них. Після цього з готовим телевізором він іде. Знайти закон розподілу часу витраченого клієнтом.

ЗАДАЧА 7

За даними групованої вибірки випадкової величини X:

1)знайти точкові й интевальные оцінки математичного сподівання Мx і дисперсії Dx з надійністю 0,95;

2) побудувати гистограмму частот;

3)перевірити гіпотезу про нормальний розподіл за допомогою критерію X2 ("хі-квадрат") при 5% рівні значимості;

4) визначити

для парних варіантів: моду, коефіцієнт асиметрії, коефіцієнт варіації.

для непарних варіантів: медіану, ексцес, лінійне відхилення.

	n1	n2	n3	n4	n5	n6	n7
N1
N2
N3
N4
N5
N6
N7
N8
N9
N10
N11
N12
N13
N14
N15
N16
N17
N18
N19
N20
N21
N22
N23
N24

N - номер варіанта,

n1 - число значень вибірки в інтервалі (N-15,N-13),

n2 - число значень вибірки в інтервалі (N-13,N-11),

n3- число значень вибірки в інтервалі (N-11,N-9),

n4 - число значень вибірки в інтервалі (N-9,N-7),

n5 - число значень вибірки в інтервалі (N-7,N-5),

n6 - число значень вибірки в інтервал (N-5,N-3),

n7 - число значень вибірки в інтервалі (N-3,N-1).

ДОДАТОК А

Таблиця А.1 – Таблиця значень функції

x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)
0.00	0. 0000	0.24	0. 0948	0.48	0. 1844	0.72	0. 2642	0.96	0. 3315
0.01	0. 0040	0.25	0. 0987	0.49	0. 1879	0.73	0. 2673	0.97	0. 3340
0.02	0. 0080	0.26	0. 1026	0.50	0. 1915	0.74	0. 2703	0.98	0. 3365
0.03	0. 0120	0.27	0. 1064	0.51	0. 1950	0.75	0. 2734	0.99	0. 3389
0.04	0. 0160	0.28	0. 1103	0.52	0. 1985	0.76	0. 2764	1.00	0. 3413
0.05	0. 0199	0.29	0. 1141	0.53	0. 2019	0.77	0. 2794	1.01	0. 3438
0.06	0. 0239	0.30	0. 1179	0.54	0. 2054	0.78	0. 2823	1.02	0. 3461
0.07	0. 0279	0.31	0. 1217	0.55	0. 2088	0.79	0. 2852	1.03	0. 3485
0.08	0. 0319	0.32	0. 1255	0.56	0. 2123	0.80	0. 2881	1.04	0. 3508
0.09	0. 0359	0.33	0. 1293	0.57	0. 2157	0.81	0. 2910	1.05	0. 3531
0.10	0. 0398	0.34	0. 1331	0.58	0. 2190	0.82	0. 2939	1.06	0. 3554
0.11	0. 0438	0.35	0. 1368	0.59	0. 2224	0.83	0. 2967	1.07	0. 3577
0.12	0. 0478	0.36	0. 1406	0.60	0. 2257	0.84	0. 2995	1.08	0. 3599
0.13	0. 0517	0.37	0. 1443	0.61	0. 2291	0.85	0. 3023	1.09	0. 3621
0.14	0. 0557	0.38	0. 1480	0.62	0. 2324	0.86	0. 3051	1.10	0. 3643
0.15	0. 0596	0.39	0. 1517	0.63	0. 2357	0.87	0. 3078	1.11	0. 3665
0.16	0. 0636	0.40	0. 1554	0.64	0. 2389	0.88	0. 3106	1.12	0. 3686
0.17	0. 0675	0.41	0. 1591	0.65	0. 2422	0.89	0. 3133	1.13	0. 3708
0.18	0. 0714	0.42	0. 1628	0.66	0. 2454	0.90	0. 3159	1.14	0. 3729
0.19	0. 0753	0.43	0. 1664	0.67	0. 2486	0.91	0. 3186	1.15	0. 3749
0.20	0. 0793	0.44	0. 7000	0.68	0. 2517	0.92	0. 3212	1.16	0. 3770
0.21	0. 0832	0.45	0. 1736	0.69	0. 2549	0.93	0. 3238	1.17	0. 3790
0.22	0. 0871	0.46	0. 1772	0.70	0. 2580	0.94	0. 3264	1.18	0. 3810
0.23	0. 0910	0.47	0. 1808	0.71	0. 2511	0.95	0. 3289	1.19	0. 3830

Продовження таблиці А.1

1.20	0. 3849	1.46	0. 4279	1.72	0. 4573	1.98	0. 4761	2.48	0. 4934
1.21	0. 3869	1.47	0. 4292	1.73	0. 4582	1.99	0. 4767	2.50	0. 4938
1.22	0. 3883	1.48	0. 4306	1.74	0. 4591	2.00	0. 4772	2.52	0. 4941
1.23	0. 3907	1.49	0. 4319	1.75	0. 4599	2.02	0. 4783	2.54	0. 4945
1.24	0. 3925	1.50	0. 4332	1.76	0. 4608	2.04	0. 4793	2.56	0. 4948
1.25	0. 3944	1.51	0. 4345	1.77	0. 4616	2.06	0. 4803	2.58	0. 4951
1.26	0. 3962	1.52	0. 4357	1.78	0. 4625	2.08	0. 4812	2.60	0. 4953
1.27	0. 3980	1.53	0. 4370	1.79	0. 4633	2.10	0. 4821	2.62	0. 4956
1.28	0. 3997	1.54	0. 4382	1.80	0. 4641	2.12	0. 4830	2.64	0. 4959
1.29	0. 4015	1.55	0. 4394	1.81	0. 4649	2.14	0. 4838	2.66	0. 4961
1.30	0. 4032	1.56	0. 4406	1.82	0. 4656	2.16	0. 4846	2.68	0. 4963
1.31	0. 4049	1.57	0. 4418	1.83	0. 4664	2.18	0. 4854	2.70	0. 4965
1.32	0. 4066	1.58	0. 4429	1.84	0. 4671	2.20	0. 4861	2.72	0. 4967
1.33	0. 4082	1.59	0. 4441	1.85	0. 4686	2.22	0. 4868	2.74	0. 4969
1.34	0. 4099	1.60	0. 4452	1.86	0. 4686	2.24	0. 4875	2.76	0. 4971
1.35	0. 4115	1.61	0. 4463	1.87	0. 4693	2.26	0. 4881	2.78	0. 4973
1.36	0. 4131	1.62	0. 4474	1.88	0. 4699	2.28	0. 4887	2.80	0. 4974
1.37	0. 4147	1.63	0. 4484	1.89	0. 4706	2.30	0. 4893	2.82	0. 4976
1.38	0. 4162	1.64	0. 4495	1.90	0. 4713	2.32	0. 4898	2.84	0. 4977
1.39	0. 4177	1.65	0. 4505	1.91	0. 4719	2.34	0. 4904	2.86	0. 4979
1.40	0. 4192	1.66	0. 4515	1.92	0. 4726	2.36	0. 4909	2.88	0. 4980
1.41	0. 4207	1.67	0. 4525	1.93	0. 4732	2.38	0. 4913	2.90	0. 4981
1.42	0. 4222	1.68	0. 4535	1.94	0. 4738	2.40	0. 4918	2.94	0. 4984
1.43	0. 4236	1.69	0. 4545	1.95	0. 4744	2.42	0. 4922	3.00	0. 49865
1.44	0. 4251	1.70	0. 4554	1.96	0. 4750	2.44	0. 4927	4.00	0. 499968
1.45	0. 4265	1.71	0. 4564	1.97	0. 4756	2.46	0. 4931	5.00	0. 499997

Таблиця А.2 – Критичні точки розподілу Стьюдента

Число ступенів свободи	Рівень значущості (двостороння критична область)
k	0.10	0.05	0.02	0.01	0. 002	0. 001
	6.31	12.7	31.82	63.7	318.3	637.0
	2.92	4.30	6.97	9.92	22.33	31.6
	2.35	3.18	4.54	5.84	10.22	12.9
	2.13	2.78	3.75	4.60	7.17	8.61
	2.01	2.57	3.37	4.03	5.89	6.86
	1.94	2.45	3.14	3.71	5.21	5.96
	1.89	2.36	3.00	3.50	4.79	5.40
	1.86	2.31	2.90	3.36	4.50	5.04
	1.83	2.26	2.82	3.25	4.30	4.78
	1.81	2.23	2.76	3.17	4.14	4.59
	1.80	2.20	2.72	3.11	4.03	4.44
	1.78	2.18	2.68	3.05	3.93	4.32
	1.77	2.16	2.65	3.01	3.85	4.22
	1.76	2.14	2.62	2.98	3.79	4.14
	1.75	2.13	2.60	2.95	3.73	4.07
	1.75	2.12	2.58	2.92	3.69	4.01
	1.74	2.11	2.57	2.90	3.65	3.96
	1.73	2.10	2.55	2.88	3.61	3.92
	1.73	2.09	2.54	2.86	3.38	3.88
	1.73	2.09	2.53	2.85	3.55	3.85
	1.72	2.08	2.52	2.83	3.53	3.82
	1.72	2.07	2.51	2.82	3.51	3.79
	1.71	2.07	2.50	2.81	3.49	3.77
	1.71	2.06	2.49	2.80	3.47	3.74
	1.71	2.06	2.49	2.79	3.45	3.72
	1.71	2.06	2.48	2.78	3.44	3.71
	1.71	2.05	2.47	2.77	3.42	3.69
	1.70	2.05	2.46	2.76	3.40	3.66
	1.70	2.05	2.46	2.76	3.40	3.66
	1.70	2.04	2.46	2.75	3.39	3.65
	1.68	2.02	2.42	2.70	3.31	3.55
	1.67	2.00	2.39	2.66	3.23	3.46
	1.66	1.98	2.36	2.62	3.17	3.37
k	0.05	0. 025	0.01	0. 005	0. 001	0. 0005
Число ступенів свободи	Рівень значущості (одностороння критична область)

Таблиця А.3 - Критичні точки розподілу

Число ступенів свободи	Рівень значущості
k	0.01	0. 025	0.05	0.95	0. 975	0.99
	6.6	5.0	3.8	0. 0039	0. 00098	0. 00016
	9.2	7.4	6.0	0. 103	0. 051	0. 020
	11.3	9.4	7.8	0. 352	0. 216	0. 115
	13.3	11.1	9.5	0. 711	0. 484	0. 297
	15.1	12.8	11.1	1.15	0. 831	0. 554
	16.8	14.4	12.6	1.64	1.24	0. 872
	18.5	16.0	14.1	2.17	1.69	1.24
	20.1	17.5	15.5	2.73	2.18	1.65
	21.7	19.0	16.9	3.33	2.70	2.09
	23.2	20.5	18.3	3.94	3.25	2.56
	24.7	21.9	19.7	4.57	3.82	3.05
	26.2	23.3	21.0	5.23	4.40	3.57
	27.7	24.7	22.4	5.89	5.01	4.11
	29.1	26.1	23.7	6.57	5.63	4.66
	30.6	27.5	25.0	7.26	6.26	5.23
	32.0	28.8	26.3	7.96	6.91	5.81
	33.4	30.2	27.6	8.67	7.56	6.41
	34.8	31.5	28.9	9.39	8.23	7.01
	36.2	32.9	30.1	10.1	8.91	7.63
	37.6	34.2	31.4	10.9	9.59	8.26
	38.9	35.5	32.7	11.6	10.3	8.90
	40.3	36.8	33.9	12.3	11.0	9.54
	41.6	38.1	35.2	13.1	11.7	10.2
	43.0	39.4	36.4	13.8	12.4	10.9
	44.3	40.6	37.7	14.6	13.1	11.5
	45.6	41.9	38.9	15.4	13.8	12.2
	47.0	43.2	40.1	16.2	14.6	12.9
	48.3	44.5	41.3	16.9	15.3	13.6
	49.6	45.7	42.6	17.7	16.0	14.3
	50.9	47.0	43.8	18.5	16.8	15.0

Значення функції 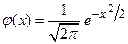Таблиця 1

x		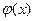x		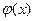x		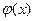x		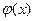x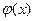
	0,3989	0,5	0,3521		0,2420	1,5	0,1295		0,0540
0,01	0,3989	0,51	0,3503	1,01	0,2396	1,51	0,1276	2,01	0,0529
0,02	0,3989	0,52	0,3485	1,02	0,2371	1,52	0,1257	2,02	0,0519
0,03	0,3988	0,53	0,3467	1,03	0,2347	1,53	0,1238	2,03	0,0508
0,04	0,3986	0,54	0,3448	1,04	0,2323	1,54	0,1219	2,04	0,0498
0,05	0,3984	0,55	0,3429	1,05	0,2299	1,55	0,1200	2,05	0,0488
0,06	0,3982	0,56	0,3410	1,06	0,2275	1,56	0,1182	2,06	0,0478
0,07	0,3980	0,57	0,3391	1,07	0,2251	1,57	0,1163	2,07	0,0468
0,08	0,3977	0,58	0,3372	1,08	0,2227	1,58	0,1145	2,08	0,0459
0,09	0,3973	0,59	0,3352	1,09	0,2203	1,59	0,1127	2,09	0,0449
0,1	0,3970	0,6	0,3332	1,1	0,2179	1,6	0,1109	2,1	0,0440
0,11	0,3965	0,61	0,3312	1,11	0,2155	1,61	0,1092	2,11	0,0431
0,12	0,3961	0,62	0,3292	1,12	0,2131	1,62	0,1074	2,12	0,0422
0,13	0,3956	0,63	0,3271	1,13	0,2107	1,63	0,1057	2,13	0,0413
0,14	0,3951	0,64	0,3251	1,14	0,2083	1,64	0,1040	2,14	0,0404
0,15	0,3945	0,65	0,3230	1,15	0,2059	1,65	0,1023	2,15	0,0396
0,16	0,3939	0,66	0,3209	1,16	0,2036	1,66	0,1006	2,16	0,0387
0,17	0,3932	0,67	0,3187	1,17	0,2012	1,67	0,0989	2,17	0,0379
0,18	0,3925	0,68	0,3166	1,18	0,1989	1,68	0,0973	2,18	0,0371
0,19	0,3918	0,69	0,3144	1,19	0,1965	1,69	0,0957	2,19	0,0363
0,2	0,3910	0,7	0,3123	1,2	0,1942	1,7	0,0940	2,2	0,0355
0,21	0,3902	0,71	0,3101	1,21	0,1919	1,71	0,0925	2,21	0,0347
0,22	0,3894	0,72	0,3079	1,22	0,1895	1,72	0,0909	2,22	0,0339
0,23	0,3885	0,73	0,3056	1,23	0,1872	1,73	0,0893	2,23	0,0332
0,24	0,3876	0,74	0,3034	1,24	0,1849	1,74	0,0878	2,24	0,0325
0,25	0,3867	0,75	0,3011	1,25	0,1826	1,75	0,0863	2,25	0,0317
0,26	0,3857	0,76	0,2989	1,26	0,1804	1,76	0,0848	2,26	0,0310
0,27	0,3847	0,77	0,2966	1,27	0,1781	1,77	0,0833	2,27	0,0303
0,28	0,3836	0,78	0,2943	1,28	0,1758	1,78	0,0818	2,28	0,0297
0,29	0,3825	0,79	0,2920	1,29	0,1736	1,79	0,0804	2,29	0,0290
0,3	0,3814	0,8	0,2897	1,3	0,1714	1,8	0,0790	2,3	0,0283
0,31	0,3802	0,81	0,2874	1,31	0,1691	1,81	0,0775	2,31	0,0277
0,32	0,3790	0,82	0,2850	1,32	0,1669	1,82	0,0761	2,32	0,0270
0,33	0,3778	0,83	0,2827	1,33	0,1647	1,83	0,0748	2,33	0,0264
0,34	0,3765	0,84	0,2803	1,34	0,1626	1,84	0,0734	2,34	0,0258
0,35	0,3752	0,85	0,2780	1,35	0,1604	1,85	0,0721	2,35	0,0252
0,36	0,3739	0,86	0,2756	1,36	0,1582	1,86	0,0707	2,36	0,0246
0,37	0,3725	0,87	0,2732	1,37	0,1561	1,87	0,0694	2,37	0,0241
0,38	0,3712	0,88	0,2709	1,38	0,1539	1,88	0,0681	2,38	0,0235
0,39	0,3697	0,89	0,2685	1,39	0,1518	1,89	0,0669	2,39	0,0229
0,4	0,3683	0,9	0,2661	1,4	0,1497	1,9	0,0656	2,4	0,0224
0,41	0,3668	0,91	0,2637	1,41	0,1476	1,91	0,0644	2,41	0,0219
0,42	0,3653	0,92	0,2613	1,42	0,1456	1,92	0,0632	2,42	0,0213
0,43	0,3637	0,93	0,2589	1,43	0,1435	1,93	0,0620	2,43	0,0208
0,44	0,3621	0,94	0,2565	1,44	0,1415	1,94	0,0608	2,44	0,0203
0,45	0,3605	0,95	0,2541	1,45	0,1394	1,95	0,0596	2,45	0,0198
0,46	0,3589	0,96	0,2516	1,46	0,1374	1,96	0,0584	2,46	0,0194
0,47	0,3572	0,97	0,2492	1,47	0,1354	1,97	0,0573	2,47	0,0189
0,48	0,3555	0,98	0,2468	1,48	0,1334	1,98	0,0562	2,48	0,0184
0,49	0,3538	0,99	0,2444	1,49	0,1315	1,99	0,0551	2,49	0,0180

Значення функції Таблиця 1 (продовження)

---

Дата добавления: 2015-10-31