Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

IV.2. Работа, теплота и внутренняя энергия в политропном процессе.

I.6. Работа и теплота. Свойства работы и теплоты. | I.7. Характеристические функции. | I.8. Дифференциальные соотношения термодинамики. | II.1. Классификация теплоемкостей по единицам количества вещества и видам процессов. | II.2. Общая формула теплоёмкостей однородных систем. | II.3. Внутренняя энергия и теплоёмкость идеального газа. | II.4. Зависимость теплоёмкостей от давления, объёма и температуры. | II.5. Зависимость теплоёмкостей от температуры. Истинная и средняя теплоёмкости. | III.1. Три группы формул для вычисления энтропии. | III.2. Уравнение адиабаты реального газа в общем виде. |


Читайте также:
  1. I.2. Теплота, работа, внутренняя энергия.
  2. I.6. Работа и теплота. Свойства работы и теплоты.
  3. II.3. Внутренняя энергия и теплоёмкость идеального газа.
  4. IV.2. Биогенные факторы
  5. IV.3. Изменение энтропии в политропном процессе.
  6. Беспокойство как энергия

Как известно, удельная абсолютная деформационная работа определяется по формуле:

Для того, чтобы найти этот интеграл, необходимо знать уравнение, связывающее давление и объем. Таким уравнением является уравнение политропы pvn=const. Запишем это уравнение развернутом виде:

, откуда

Тогда

Окончательно

(143)

Так как в политропном процессе газ считается идеальным, то преобразуем (143) к виду:

Или окончательно:

(144)

Получим ещё несколько формул для Аn, для чего подставим в (144) , найденные из других уравнений политропы. Из уравнения

 

 

 

(144*)
Тогда

(145)

Из уравнения следует

Или

(146)

После подстановки (146) в (144) окончательно получим

(147)

Формула (147) широко используется в теории газовых турбин, газовой динамике и так далее.

Внутренняя энергия идеального газа зависит только температуры, поэтому соотношение (73) для идеального газа примет вид

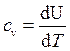, (148)

откуда после интегрирования при сv =const

(149)

Формула (148) справедлива для любого процесса, в том числе и для политропного, поэтому

(150)

Как известно

, откуда для политропного процесса

dQn=cndT (151)

После подстановки (142) в (151) и интегрирования при окончательно получим:

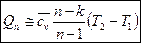(152)

 

Дата добавления: 2015-09-01; просмотров: 103 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
IV.1. Уравнение политропы. Определение показателя политропы.| IV.3. Изменение энтропии в политропном процессе.
mybiblioteka.su - 2015-2024 год. (0.006 сек.)