
Читайте также:
|
Опытные значения зависимости теплоёмкостей от температуры представляются в виде таблиц, графиков и эмпирических зависимостей. У большинства технических газов cv и cp возрастают с ростом температуры.
Из физики известно, что температура газа не связана колебательным движением атомов и молекул, а зависит от кинетической энергии их поступательного движения. Подводимая к газу теплота по мере роста температуры перераспределяется всё более и более в пользу колебательного движения и поэтому прирост температуры на одинаковый подвод теплоты замедляется.

На рис.8 опытные данные обозначены в виде звездочек. Сплошная линия – аппроксимирующая их кривая, подчиняющаяся уравнению
c=c0 + at + bt2 + dt3 +… (93)
Здесь c0, a, b, d и т.д – эмпирические коэффициенты (коэффициенты, полученные опытным путем). Аппроксимирующая кривая проводится с использованием метода наименьших квадратов или других аналогичных математических методов. В инженерных расчетах ограничиваются первыми двумя слагаемыми в правой части (93), то есть полагают зависимость теплоемкости от температуры линейной:
c=c0 + at (94)
В частности
cv=c0v + at (95)
cр=c0р + at (96)
Все ранее полученные формулы, включая 94,95,96, относятся к истинной теплоемкости, то есть теплоемкости для конкретной (заданной) температуры
В практических расчётах часто требуется знать среднее значение теплоёмкостей в заданном интервале температур от t1 до t2
Обозначим среднюю теплоемкость как  , или
, или 
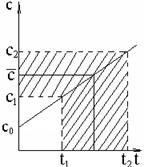 Средняя теплоемкость, в соответствие с рис.9
Средняя теплоемкость, в соответствие с рис.9
определяется как средняя линия трапеции.




 С учетом (94)
С учетом (94)
|

 =
= 
или окончательно
 (97)
(97)
Конкретные значения С0 и а содержатся в справочной литературе по теплофизическим характеристикам веществ. Связь между средним и истинным теплоемкостями выражается формулой
 (98)
(98)
В тех случаях, когда зависимость теплоёмкости от температуры не удаётся удовлетворительно аппроксимировать зависимостью c=c0+at, можно воспользоваться формулой для нелинейной зависимости:
 (99)
(99)
Для оценочных (не очень точных) расчетов, когда отсутствуют опытные данные для теплоемкости в виде таблиц или эмпирических формул, можно воспользоваться результатами молекулярно-кинетической теории газов.
Из молекулярно-кинетической теории газов известно соотношение
Um = 12,56T 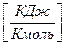 (100)
(100)
Здесь Um - внутренняя энергия одного киломоля идеального газа, Т - абсолютная термодинамическая температура, К.
Для массовой изохорной теплоемкости идеального газа, ранее было получено (73):
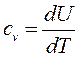
Так как  и
и  , то молярная изохорная теплоемкость равна
, то молярная изохорная теплоемкость равна
 (101)
(101)
Подставляя (100) в (101) получим
 (102)
(102)
Молярную изобарную теплоемкость сµp найдем из уравнения Майера: cmp - cmv = Rm = 8,314  , откуда
, откуда
cmp=cmv+Rm=12,56+8,314 @ 20,93  (103)
(103)
Как следует из (102) и (103), по молекулярно-кинетической теории газов теплоемкости не зависят от температуры, то есть берутся средним значением и во всем диапазоне температур. Именно в этом заключается оценочный характер этих значений.
Понятию идеального газа в большей степени соответствуют одноатомные газы при малых давлениях. На практике же, чаще всего приходится иметь дело с двухатомными, трехатомными и более атомными газами.
Например, воздух – двухатомный газ, так как он по объёму на 79% состоит из азота (N2) и на 21% из кислорода (O2).
Для оценочных расчетов можно пользоваться следующей таблицей:
| Газ | cmv, 
| cmp, 
|
| Одноатомный |  12,56 12,56
| 20,93 |
| Двухатомный | 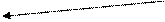 20,93 20,93
| 29,31 |
| Трех и более атомный | 29,31 | 37,68 |
Примечание: в этой таблице, во второй и третьей строчках теплоемкости скорректированы по результатам опытов.
У реальных газов, в отличие от идеального, теплоёмкости могут зависеть не только от температуры, но и от объёма и давления.
Дата добавления: 2015-09-01; просмотров: 351 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| II.4. Зависимость теплоёмкостей от давления, объёма и температуры. | | | III.1. Три группы формул для вычисления энтропии. |