Периодические функции.

Периодическая функция ― функция, повторяющая свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода функции).

Говоря более формально, функция периодична, если существует такое число T≠0 (период), что на всей области определения функции выполняется равенство .

Все тригонометрические функции являются периодическими.

Формальное определение

Пусть есть абелева группа (обычно предполагается — вещественные числа с операцией сложения или 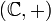— комплексные числа). Функция (где — произвольное множество её значений) называется периодической с периодом , если справедливо

.

Если это равенство не выполнено ни для какого , то функция называется апериодической.

Если для функции существуют два периода , отношение которых не равно вещественному числу, то есть , то называется двоякопериодической функцией. В этом случае значения на всей плоскости определяются значениями в параллелограмме, натянутом на .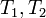

Замечание

Период функции определён неоднозначно. В частности, если — период, то и любой элемент вида (или , если в области определения функции определена операция умножения), где — произвольное натуральное число, также является периодом.

Множество всех периодов функции образует аддитивную группу.

Однако если у множества периодов имеется наименьшее значение, то оно называется основным (или главным) периодом функции.

Примеры

• Вещественные функции синус и косинус являются периодическими с основным периодом , так как

• Функция, равная константе , является периодической, и любое ненулевое число является её периодом. Основного периода функция не имеет.

• Функция Дирихле является периодической, её периодом является любое ненулевое рациональное число. Основного периода она также не имеет.

• Функция является апериодической.

Некоторые особенности периодических функций

• Сумма двух функций с соизмеримыми периодами и не всегда является функцией с основным периодом, равным наименьшему общему кратному и (однако просто периодом это число будет являться). Например, у функции основной период равен , у функции 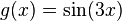— , а у их суммы основной период, очевидно, равен .

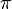• Сумма двух функций с несоизмеримыми периодами не всегда является непериодической функцией. Например, функция из предыдущего примера и функция имеют несоизмеримые периоды, но их сумма равна константе, а значит, является периодической функцией.

• Существуют периодические функции, не равные константе, у которой периодами являются несоизмеримые числа. Например, у функции , принимающей значения 1 при алгебраическом x и 0 в остальных случаях, любое алгебраическое число является периодом, а среди алгебраических чисел есть и несоизмеримые.

Дата добавления: 2015-09-01