Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Нормальные уравнения

Решение нормальных уравнений способом обращения | Оценка точности по материалам уравнивания | Блок-схема параметрического способа уравнивания | Уравнивание нивелирной сети параметрическим способом | Оценку точности параметров и функции параметров выполним с использованием элементов обратной матрицы | Уравнивание углов на станции параметрическим способом | Систему нормальных уравнений решим методом обращения | Оценим точность результатов измерений. |


Читайте также:
  1. I.4. Состояния системы. Уравнения состояния системы.
  2. Аналитическое решение дифференциального уравнения
  3. Всякая лин. Комбинация решений ЛОДУ является решением этого уравнения или системы.
  4. Вывод дифференциального уравнения
  5. Вывод уравнения
  6. Графический способ решения IRR — уравнения
  7. Дифференциальные уравнения с разделяющимися переменными

Параметрические уравнения поправок решают по МНК, т.е. под условием [pv²] = min, в результате чего получают систему нормальных уравнений:

NttXt1 + Bt1 = 0 (30)

Здесь

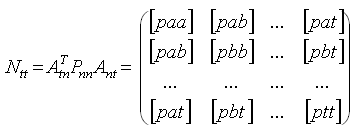
- матрица коэффициентов нормальных уравнений.

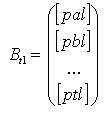
- вектор свободных членов.

Представим систему нормальных уравнений в обычном алгебраическом виде:

(31)

Дата добавления: 2015-09-02; просмотров: 56 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Обозначим| Составление нормальных уравнений
mybiblioteka.su - 2015-2024 год. (0.006 сек.)