Обозначим

Параметрический способ уравнивания

Параметрические уравнения

Пусть выполнено n измерений у₁, у₂,..., у_n с весами p₁, p₂,..., p_n; t - число необходимых измерений. Выбирают t независимых неизвестных - параметров - х₁, х₂,..., х_t. Это могут быть измеряемые и неизмеряемые (отметки, координаты определяемых пунктов) величины. Y₁, Y₂,..., Y_n - истинные значения измеренных величин; Х₁, Х₂,..., Х_t - истинные значения параметров. Между этими значениями может быть установлена исходная система параметрических уравнений связи, в которой измеренные величины представлены в виде функций выбранных параметров

F_i(X₁, X₂,..., X_t) = Y_i, (i = 1, 2,..., n). (25)

С уравненными значениями измеренных величин и параметров система (25) принимает вид:

F_i(x₁, x₂,..., x_t) = y_i + ν_i, (i = 1, 2,..., n).

Или

F_i(x₁, x₂,..., x_t) - y_i = ν_i, (i = 1, 2,..., n). (26)

Функции F_i приводят к линейному виду разложением в ряд Тейлора. С этой целью вводят приближенные значения параметров х⁰₁, x⁰₂,..., x⁰_t, которые вычисляют по результатам измерений. Тогда

x_j = x⁰_j + δx_j, (j = 1, 2,..., t), (27)

где δх_j - поправки к приближенным значениям параметров.

На основании (26) с учетом (27) будем иметь:

Обозначим

- свободные члены параметрических уравнений поправок;

- коэффициенты параметрических уравнений поправок;

(28)

- параметрические уравнения поправок.

Систему (28) запишем в матричном виде:

А_ntX_t1 + L_n1 = V_n1, (29)

Где

- матрица коэффициентов; - вектор поправок к приближенным значениям параметров;

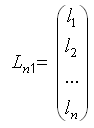- вектор свободных членов; - вектор поправок к результатам измерений.

Дата добавления: 2015-09-02