Уравнивание углов на станции параметрическим способом

В табл. 13 даны результаты равноточных измерений углов на станции (рис. 4).

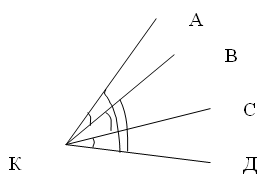
Рис. 4. Углы на станции

Таблица 13

Результаты измерений β_i

№ углов	Углы	βi	№ углов	Углы	βi
	АКВ	20° 00′ 05,2″		АКД	65° 20′20,0″
	ВКС	20° 00′ 10,1″		ВКД	45° 20′ 05,0″
	СКД	25° 20′ 00,0″

Число всех измеренных углов n = 5; число необходимых измерений t = 3.

Выберем в качестве параметров х₁, х₂, х₃ соответственно первый, второй, третий углы. Четвертый и пятый углы можно представить как суммы параметров.

Составим параметрические уравнения связи по формуле:

F_i(x₁, x₂,..., x_t) - y_i = ν_i, (i = 1, 2,..., n).

(40)

Введем приближенные значения параметров, приняв их равными измеренным значениям соответствующих углов:

х₁⁰ = 20°00′05,2″; х₂⁰ = 20°00′10,1″; х₃⁰ = 25°20′00,0″.

x_j = x_j⁰ + δx_j, (j = 1, 2, 3).

Перейдем к параметрическим уравнениям поправок:

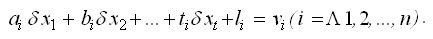
Вычислим свободные члены этих уравнений l_i = F_i(x₁⁰, x₂⁰,..., x_t⁰) - y_i.

Составим нормальные уравнения:

или N_tt X_t1 + B_t1 = 0.

Bычислим коэффициенты и свободные члены нормальных уравнений (табл. 14).

Таблица 14

Таблица параметрических уравнений

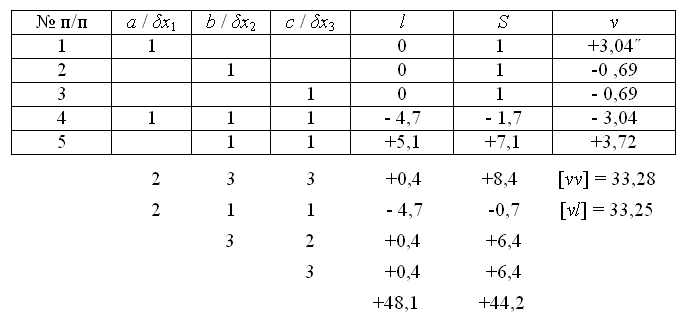
Дата добавления: 2015-09-02