Читайте также:
|
а) Решить уравнение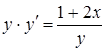 
.
Решение. Это уравнение с разделяющимися переменными. Преобразуем его: 
.
Разделяя переменные, получим:
.
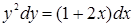Теперь интегрируем:
,
откуда 
; положим 
, тогда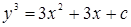 
.
Общее решение будет иметь вид
.
б) Найти частное решение дифференциального уравнения 
,
удовлетворяющее начальным условиям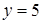 
при х =2.
Решение. 1) Находим сначала общее решение:
; 
;
откуда 
.
Приняв 
, получим
- это общее решение данного дифференциального уравнения.
2) Найдем частное решение. Для этого вычислим 
при 
.
, откуда 
.
Частное решение 
.
Дата добавления: 2015-09-02; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи на вычисление площадей | | | Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. |