Решение типовых задач. 1. В прямоугольной системе координат Oxyz точка М имеет координаты

1. В прямоугольной системе координат Oxyz точка М имеет координаты . Найти координаты ее радиус-вектора .

Решение. Абсцисса 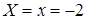, ордината , аппликата . Следовательно, . Радиус-вектор лежит в плоскости xОу.

2. Найти координаты X, Y, Z суммы векторов .

Решение. .

Следовательно, сумма векторов . Искомый вектор параллелен плоскости yOz так как его компонента по оси Оx равна нулю.

3. Найти сумму векторов .

Решение. . Результат запишем так: . Вектор 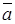коллинеарен с осью оу.

4. Найти координаты вектора 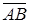, если и .

Решение. . Следовательно, .

5. Найти длину вектора 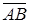, если и .

Решение. Воспользовавшись формулой , получим .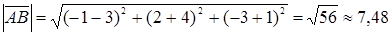

6. Найти скалярное произведение векторов , .

Решение. Скалярное произведение векторов найдем по формуле: . Получаем .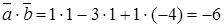

7. Найти угол между векторами и .

Решение. Воспользуемся формулой:

.

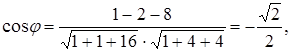
отсюда

Дата добавления: 2015-09-02