Решение типовых задач. Решение. Для нахождения предела данной функции заменим аргумент его предельным

1. Найти .

Решение. Для нахождения предела данной функции заменим аргумент его предельным значением:

.

2. Найти .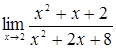

Решение. Проверим, не обращается ли знаменатель дроби в нуль при : имеем 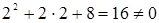. Подставив предельное значение аргумента, находим

.

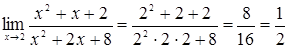3. Найти .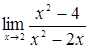

Решение. Здесь имеем неопределенность типа . Для того, чтобы раскрыть эту неопределенность, разложим числитель и знаменатель дроби на множители и до перехода к пределу сократим дробь на множитель . В результате получим .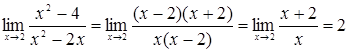

4. Найти .

Решение. Здесь пределы числителя и знаменателя при 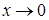равны 0. Умножив числитель и знаменатель на выражение, сопряженное числителю, получим

5. Найти

Решение. При имеем неопределенность вида . Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на 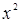. Тогда получим

6. Найти .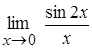

Решение. Здесь для раскрытия неопределенности применим первый замечательный предел .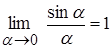

7. Найти

Решение. Имеем

.

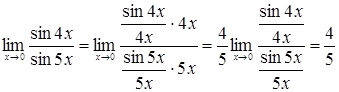8. Найти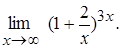

Решение. Имеем неопределенность вида . Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом

.

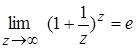Получаем .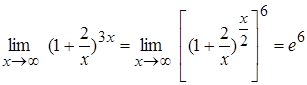

Дата добавления: 2015-09-02