Читайте также:
|
При классическом определении за вероятность события А, принимается отношение числа т исходов, благоприятствующих этому событию, к общему числу n равновозможных, единственно возможных и несовместных исходов испытания
.
При непосредственном вычислении вероятностей часто используются формулы комбинаторики.
Перестановками называются комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их следования. Число возможных перестановок
, где 
.
Примеры.
.
Размещениями называются комбинации, составленные из п различных элементов по т элементов и отличающиеся либо составом элементов, либо их порядком.
Число возможных размещений
.
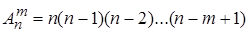Примеры.
.
Сочетаниями называются комбинации, составленные из п различных элементов по т элементов, которые отличаются хотя бы одним элементом.
Число сочетаний
.
Примеры.
.
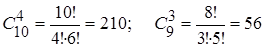Суммой событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В. Обозначение: 
.
Произведением двух событий А и В называется событие С, состоящее в появлении события А и события В. Обозначение: 
.
Теорема сложения: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Теорема умножения: 1)Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:
.
2) Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого:
.
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез)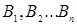 
, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую вероятность события А:
.
Это равенство называют формулой полной вероятности.
Для определения вероятности события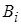 
при условии, что событие А уже произошло, используется формула Байеса:
.
Дата добавления: 2015-09-02; просмотров: 43 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Примеры для самостоятельного решения | | | Решение типовых задач |